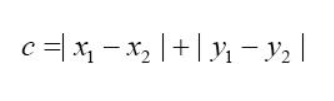欧式距离
公式为:
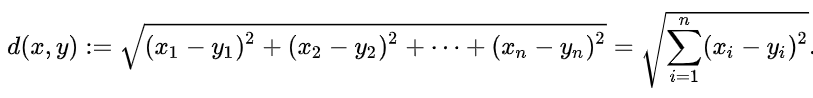
闵可夫斯基距离Minkowski
是欧氏空间中的一种测度,被看做是欧氏距离的一种推广,公式为:
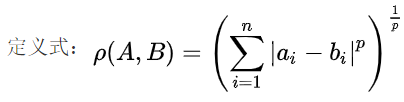
闵可夫斯基距离公式中,当时,即为欧氏距离;当p=1时,即为曼哈顿距离;当p趋于无穷时,即为切比雪夫距离。
规范化的欧几里得距离
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
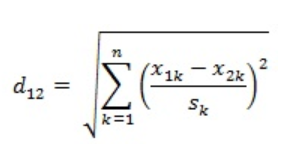
其中SK是分量的标准差
切比雪夫距离
不知道有什么卵用,不过可以转化为曼哈顿
曼哈顿距离
也叫出租车距离,用来标明两个点在标准坐标系上的绝对轴距总和
角距离
角距离,是由一定点到两物体之间所量度的夹角
余弦距离
欧式距离体现的是距离上的绝对差异,余弦距离体现的是方向上的相对差异
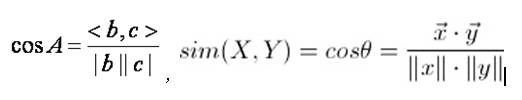
杰卡德距离Jaccard
杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标,它是杰卡德相似系数的补集,被定义为1减去Jaccard相似系数。而杰卡德相似系数(Jaccard similarity coefficient),也称杰卡德指数(Jaccard Index),是用来衡量两个集合相似度的一种指标。

马氏距离
表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧式不同的是,它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。

其中Σ是多维随机变量的协方差矩阵,μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离
但是要求协方差矩阵必须满秩,而且不能处理非线性流形上的问题