分类
分类指预测一个给定的无标签点的类标签
什么是贝叶斯分类?
贝叶斯分类器使用贝叶斯定理来预测使得后验概率最大的类标签,主要任务是估计每一个类的联合概率密度函数,并通过多元正态分步来建模
令训练数据集 D 包含 n 个 d 维空间中的点Xi , 也就是说有n个样本数据,d个指标;令 yi 表示每个点的类标签,即最终预测的类别,其中yi={c1,c2,c3,c4,,,,,,,,,ck}
贝叶斯分类器直接使用贝叶斯定理来预测一个新的实例 x 的类别 y 。它对每个类别 ci 估计后验概率 P( ci | x ) ,并选择具有最大概率的类。x的预测类为:

可以利用贝叶斯定理,将后验概率用似然和先验概率表示如下:
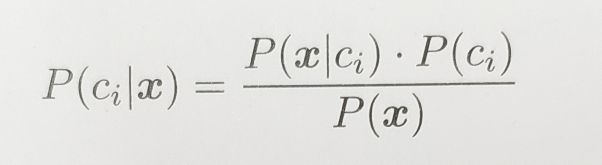
其中P( x | ci) 是似然,定义为假设真实类是ci时观察到x的概率。P(ci) 是类ci的先验概率,P( x ) 是从k个任意一个观察到x 的概率,即
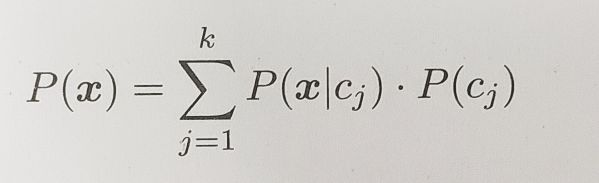
对于一个给定的点,P( x )是固定的,因此第一个公式可以重写为:
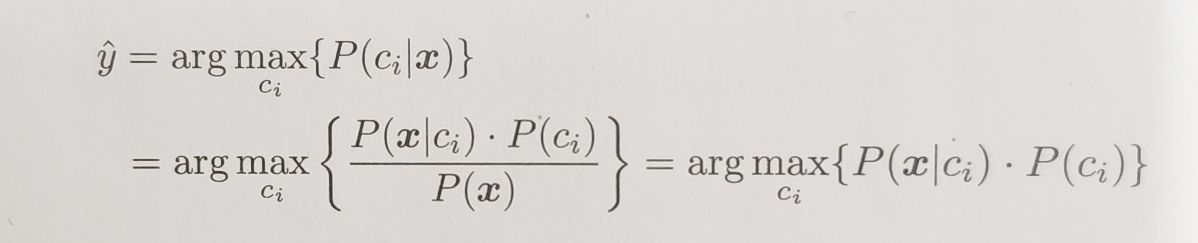
伪代码如下:

什么是朴素贝叶斯?
上面看到的完整的贝叶斯方法会遇到很多关于估计的问题,尤其是在维度比较高的情况下。朴素贝叶斯方法提出了一个简单的假设,即所有的属性都是彼此独立的。这样可以得到一个大大简化但实际上出人意料地高效的分类器。独立性假设意味着似然可以分解为每一维上的概率的乘积:
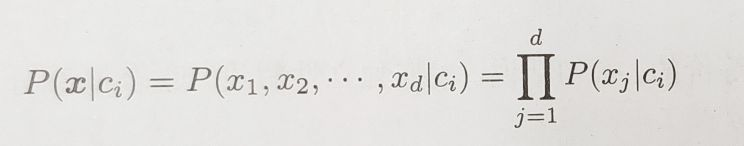
伪代码为:

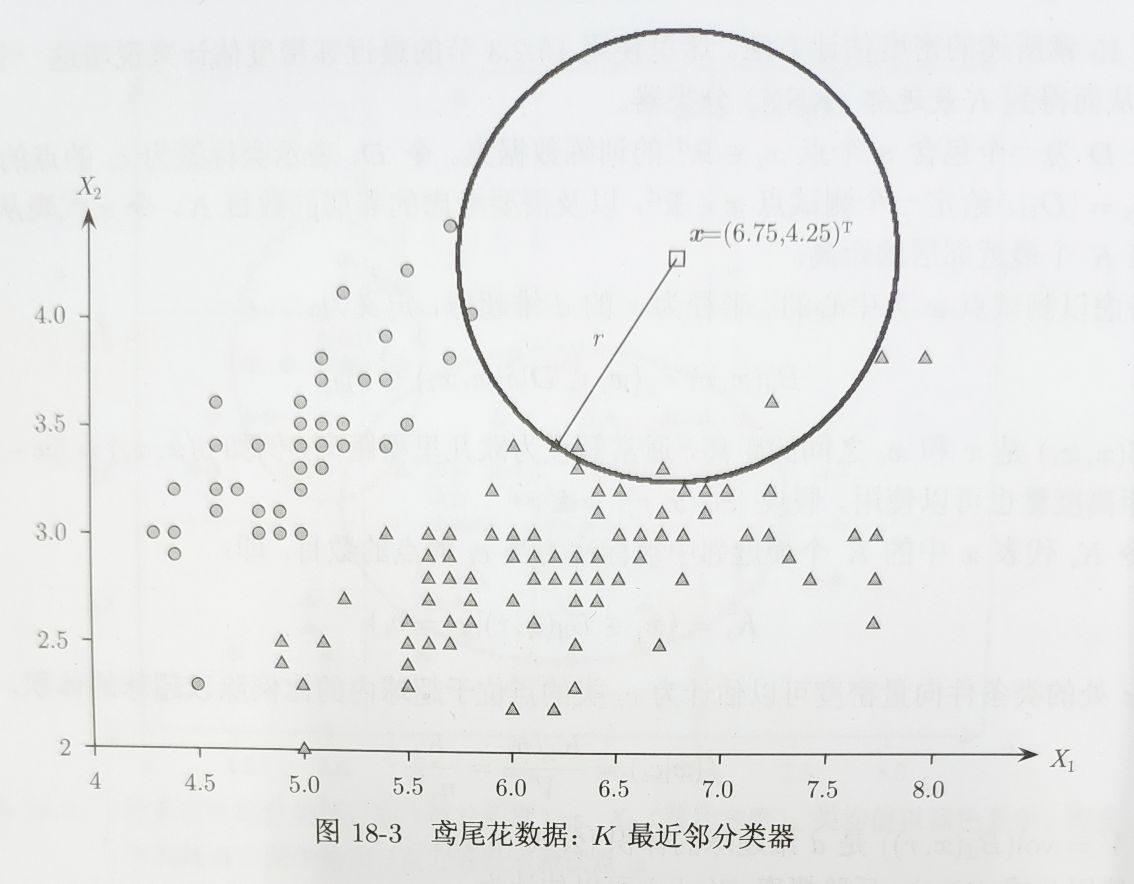
什么是K最近领分类器:
在以预测目标 x 为中心的超球体内,哪一个类的样本点的数量最多,就为预测结果