简单的中心扩散算法,就不再赘述,但是看了官方题解中的马拉车,想到,其实中心扩散是可以优化到on时间复杂度的,尤其是在大数量级字符串时,先上对比图,字符串长度为100w和1000w,随机非回文长度和回文长度为1k、1k和1w、1w,上下分别为笔者算法和马拉车算法

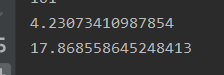
思路就是,如普通中心扩散算法一样,仅遍历一遍,但既然是求最长回文串,那么长度不需要回退,记录下当前最长的半径长度,在遍历下一个字符时,(重点1)直接套用最长半径,然后判断半径内的字符是否对称,然后从最长半径开始增长(重点2)如果从中心点开始扩张,那会走很多弯路,因为绝大部分情况下,是无法扩张到最长半径的,因此,从最长半径往中心点开始检测,在数据量足够大或者字符类型足够多时,非回文串的相同的概率越低,效果越显著,下图是60个随机ascii字符的运行时间,单位s
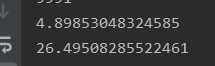
1 class Solution(object): 2 def longestPalindrome(self, s): 3 len_longest = 0 4 left = 0 5 right = 0 6 radius = 0 7 if 1 == len(s) or 0 == len(s): 8 return s 9 10 temp_symmetry = [s[0], s[1]] 11 12 len_s = len(s) 13 for i in range(len_s): 14 if i + 1 < len_s: 15 if s[i] == s[i + 1]: 16 [temp_left, temp_right, temp_len, temp_radius] = self.handle(s, i, i + 1, radius) 17 if temp_len > len_longest: 18 len_longest = temp_len 19 left = temp_left 20 right = temp_right 21 radius = temp_radius 22 23 if i >= 2: 24 if temp_symmetry[0] == s[i]: 25 [temp_left, temp_right, temp_len, temp_radius] = self.handle(s, i - 1, i - 1, radius) 26 if temp_len > len_longest: 27 len_longest = temp_len 28 left = temp_left 29 right = temp_right 30 radius = temp_radius 31 temp_symmetry.pop(0) 32 temp_symmetry.append(s[i]) 33 34 # print(left) 35 # print(right) 36 print(radius) 37 return s[left:right + 1] 38 39 def handle(self, s, left, right, radius): 40 right = right + radius 41 left = left - radius 42 len_left = left 43 len_right = len(s) - right - 1 44 45 if len_left < 0 or len_right < 0: 46 return [-1, -1, -1, -1] 47 48 for i in range(0, radius + 1): 49 if s[left + i] != s[right - i]: 50 return [-1, -1, -1, -1] 51 52 if 0 == len_left and 0 == len_right: 53 return [left, right, right - left + 1, radius] 54 55 len_min = min(len_left, len_right) 56 ori_left = left 57 ori_right = right 58 for i in range(1, len_min + 1): 59 if s[ori_left - i] == s[ori_right + i]: 60 left -= 1 61 right += 1 62 radius += 1 63 else: 64 break 65 return [left, right, right - left + 1, radius]