2019ICPC上海Spanning Tree Removal构造题

刚打完2021杭电多校6，有个构造，当时没有做，回头看了一波巨佬的博客学了一手，在这里记录一下
题目链接

链接：https://ac.nowcoder.com/acm/contest/4370/D
来源：牛客网
spj

题目描述

Bob has recently learned algorithms on finding spanning trees and wanted to give you a quiz.

To recap, a spanning tree is a subset of graph {G}G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected. Given an arbitrary undirected simple graph (without multiple edges and loops), a spanning tree removal is defined as: retrieve one spanning tree of the graph, and remove all the edges selected by the spanning tree from the original graph, obtaining a new graph.

Bob found "spanning tree removal’’ so fun that he wanted to do it over and over again. In particular, he began with a complete graph, i.e., a graph with every pair of distinct vertices connected by a unique edge. Your goal, is to smartly choose spanning trees to remove so that you can repeat as many times as possible until there is no longer a spanning tree in the graph.

输入描述:

输出描述:

示例1
输入

3
2
3
4

输出

Case #1: 1
1 2
Case #2: 1
3 1
1 2
Case #3: 2
1 3
3 4
2 4
3 2
1 4
2 1

本题是一个spj的问题
题意是给定一个完全图，包含了n个节点，每次可以在这个图中选择一个生成树，然后将该生成树的所有边都删除，然后得到一个新图，然后再从新的图中重复上述操作，问最多可以操作多少次，对于每一次操作，输出选择的生成树中的所有边(n-1行)

在lc哥的图中稍加改造，做成这个样子：
图中有6个点，将点按照0 -> 5编号

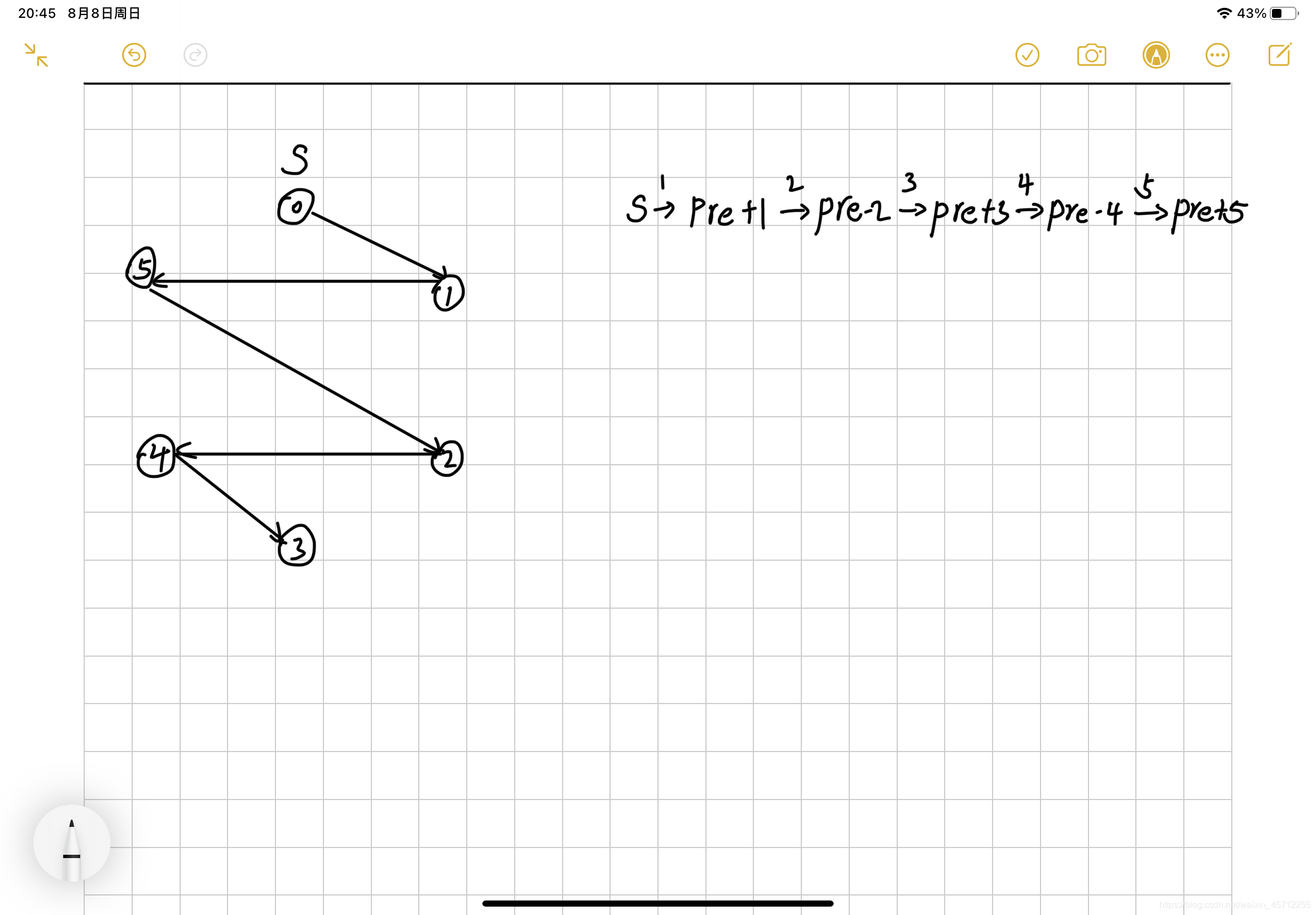
pre指的是上一个到达的节点编号
比如我们选择从0结点开始
0 -> 0 + 10 -> 1
1 -> 1 - 21 -> 5
5 -> 5 + 35 -> 2
2 -> 2 - 42 -> 4
4 -> 4 + 54 -> 3
注意这里有个( +n)%n的过程
由于节点从1开始编号，所以说，我们将左右两边+1即可
对于最多可以操作多少次的问题，我们可以从起点的选择来进行考虑，其中有n个节点，去掉重复的一半，只会有n/2(下取整)个
比如在上面有6个点的图中，从0开始和从3开始得到的图是一样的

code:

#include <iostream>

using namespace std;
#define in(x) cin>>x
typedef long long ll;

int main(){
    int _;in(_);
    int cnt = 0;
    while(_--){
        int n;in(n);
        ++ cnt;
        printf("Case #%d: %d
",cnt,n>>1);
        for(int i=1;i<=n/2;i++){
            int pre = i;
            int sign = 1;
            int now = i;
            for(int j=1;j<=n-1;j++){
                pre = now;
                now = (pre + sign * j + n) % n;
                printf("%d %d
",pre+1,now+1);
                sign *= -1;
            }
        }
    }
    
    return 0;
}