2021-07-21训练日记upc联通数(思维)|赛博朋克(唯一分解)

A. 联通数

题目描述

数学高手小G最近发现了一种新型的数！
他首先在草稿纸写下任意长度的数字串kkkkkkkkkkk…(1≤k≤9)并在其中间添加加号，且相邻两个加号之间至少含有两个数字k (默认数字串第一个数字前与最后一个数字后也有两个加号)，然后对其进行求和得出一个新的数。像这样得出的数他将其定义为 “k联通数 ” 。
小G对于他的发现感到非常的自豪， 像数字854就能表示为77+777，因此854是7联通数。
小G现在非常好奇， 究竟有哪些数可以是k联通数呢？他想考验一下你。
询问T次，每次给定两个数n,k，判断 n是否为k联通数， 如果是，输出 YES，否则出 NO。

输入

第一行一个整数T，表示询问个数。
接下来T行，每行两个整数n,k，意义如上所示。

输出

T行，每行输出 YES 或 NO。

样例输入

3
854 7
111 2
554 2

样例输出

YES
NO
YES

提示

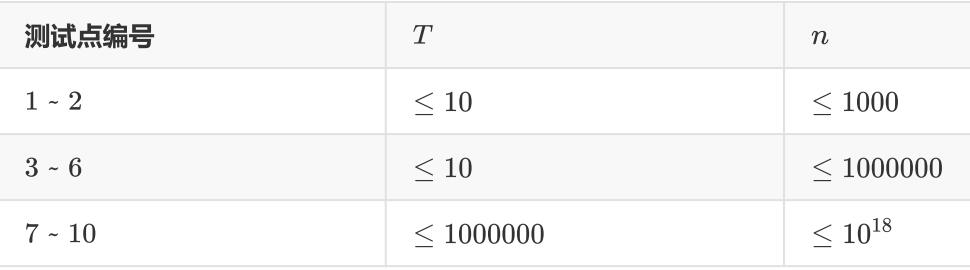
通过题意可以看到：
如果n是k联通数，那么一定可以得到 n % k == 0，反之就不是k联通数

在n % k == 0的情况下{
如果n / k是11 111这种相加组成的，那么一定就是YES，反之就是NO
到这里就和cf一个题很相似：链接
该题对应题解：链接
如果可以由11 111这种组成就是YES，反之就是NO
}
Code:

int main() {
    ll _ = read;
    while(_ --) {
        ll n = read,k =  read;
        if(n == 0) {
            puts("NO");
            continue;
        }
        if(n % k == 0) {
            ll t = n / k;
            int flag = 0;
            for(itn i=0; i*111<=t; i++) {
                if((t - i*111) % 11 == 0) {
                    flag = 1;
                    break;
                }
            }
            if(flag) puts("YES");
            else puts("NO");
        } else puts("NO");
    }
    return 0;
}
/**
 
 
 
 
**/
 
/**************************************************************
    Problem: 20006
    Language: C++
    Result: 正确
    Time:318 ms
    Memory:17656 kb
****************************************************************/

B. 赛博朋克

题目描述

在遥远的公元前65536世纪，β星座的焃碁星人发现了地球，他们对于该星球上碳基生物的大脑构造感到非常的好奇， 在植入了夸克级别的神经元控制器后， 他们夺取了所有生物大脑内惊人的算力，进而控制了所有的生物。
几亿年以后， 人类凭借着自己贫瘠的算力， 造出了庞大而惊人的超大规模集成电路，他们训练的AlphaPenguin 系统经过了几亿亿的和棋训练， 已经达到了与焃碁星人相同的智力水准。
AlphaPenguin在企图破译焃碁星人的最高权限密码，夺回所有生物的算力控制权时， 发现焃碁星人采用了以下的动态加密方式：

比起焃碁星人，AlphaPenguin由于没有足够的算力而对此感到无能为力。因此它采用了分布式计算的方法，将一小部分任务交给了你做。
具体地，你现在得到了n个数， 你需要求出这n个数中所有任意两个数的最小公倍数的最大公因数， 并把答案返回给AlphaPenguin。

输入

第一行一个整数n，表示你得到的数的个数。
第二行n个整数，a1,a2,…,an表示每个数的大小。

输出

一行，一个整数，表示你计算出的结果。

样例输入

【样例1】
4
10 24 40 80
【样例2】
10
540 648 810 648 720 540 594 864 972 648

样例输出

【样例1】
40
【样例2】
54

提示

样例解释
在第一个样例中，lcm(10,24)=120,lcm(10,40)=40,lcm(10,80)=80,lcm(24,40)=120,lcm(24,80)=240,lcm(40,80)=80，gcd(120,40,80,120,240,80)=40,因此答案即为40。

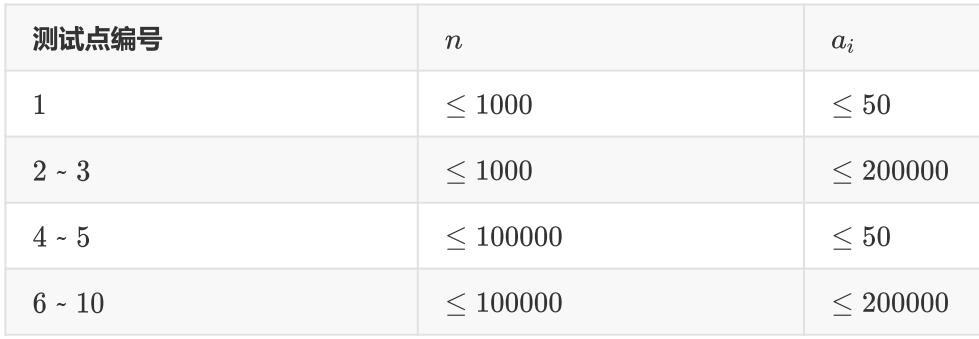
首先通过提议我们可以知道，这个题让求的是任意两个数的lcm的gcd
根据lcm,gcd定义我们可以知道：

在这里先将求完lcm，再求gcd的结果记为x
看样例{
4
10 24 40 80
10 == 2¹ * 3⁰ * 5¹
24 == 2³ * 3¹ * 5⁰
40 == 2³ * 3⁰ * 5¹
80 == 2⁴ * 3⁰ * 5¹
①对于2的次方数中，对答案x的贡献一定是次小的那个次方数(2^3)
②对于3的次方数中，对答案x不会产生贡献(因为只有一个数有三的次幂)
③对于5的次方数中，对答案x的贡献是因子中有5且次方数最小的那个(5^1)
答案x == ①2 ^ 3 * ③5 ^ 1 == 40
所以我们可以看到，将这n个数唯一分解之后，有这个数的幂次的数量为 >= n - 1才可以
数量 == n的时候，贡献是次小的幂次
数量 == n - 1的时候，贡献是最小的那个幂次
这个时候对每一个质因子的次方数维护在对应的优先队列(小根堆)里面就好啦
}
code:

typedef int itn;
ll prime[maxn],tot;
bool vis[maxn];
void getPrime() {
    memset(vis,0,sizeof(vis));
    tot = 0;
    for(int i=2; i<=maxn; i++) {
        if(!vis[i]) prime[++tot] = i;
        for(int j = 1; j <= tot && i * prime[j] <= maxn; j ++) {
            vis[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
        }
    }
}
ll p[maxn],a[maxn],cnt;
void get(ll n) {
    cnt = 0;
    for(int i=1; prime[i] * prime[i] <= n; i++) {
        if(n % prime[i] == 0) {
            p[++cnt] = prime[i];
            a[cnt] = 0;
            while(n % prime[i] == 0) {
                a[cnt]++;
                n /= prime[i];
            }
        }
        if(n == 1) break;
    }
    if(n > 1) p[++cnt] = n,a[cnt] = 1;
}
ll num[maxn];
priority_queue <int, vector<int>, greater<int> > que[maxn];
int main() {
    getPrime();
    int n = read;
    for(int i = 1; i <= n; i ++) num[i] = read;
    for(int i = 1; i <= n; i ++) {
        get(num[i]);
        for(int j = 1; j <= cnt; j++) {
            ///vet[i].push_back({p[j],a[j]});
            que[p[j]].push(a[j]);
            ///cout<<p[j]<<' '<<a[j]<<endl;
        }
    }
    ll ans = 1LL;
    for(int i = 0; i <= maxn; i++) {
        if(que[i].size() == n - 1) {
            ll p = que[i].top();
            ans *= qPow(i,p);
        }
        else if(que[i].size() == n) {
            que[i].pop();
            ans *= qPow(i, que[i].top());
        }
    }
    cout << ans <<endl;
    return 0;
}
/**
10
540 648 810 648 720 540 594 864 972 648
 
4
10 24 40 80
 
**/
 
/**************************************************************
    Problem: 20007
    Language: C++
    Result: 正确
    Time:312 ms
    Memory:68408 kb
****************************************************************/