欢迎浏览我的个人博客
转载请注明出处 https://pushy.site
1. 树
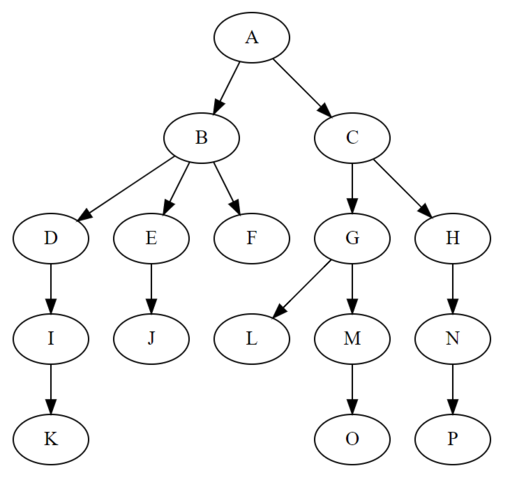
我们都知道,树是一种一对多的数据结构,它是由n个有限节点组成的一个具有层次关系的集合,它有如下的特点:
- 根节点是唯一的(老大当然是一个~);
- 每个节点都有零个或者必须多个子节点(丁克、独生子、双胞胎、三胞胎...);
- 每一个非根节点有且只有一个父节点(只有一个老爹,没有老王)
如下图,A即是根节点:
2. 二叉树
从名字和图中可以看出,二叉树应该是一种特殊形式的树:
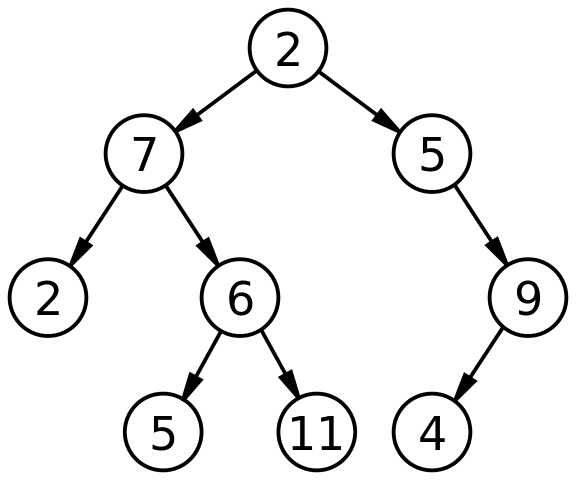
没错!它和树相比,有一下的自己的特点:
-
每个节点最多有两颗树(可以丁克,可以独生子,可以双胞胎,但是不允许三胞胎、四胞胎...);
-
左子树和右子树是有顺序的,次序不能任意颠倒(老大老二分明);
-
即使树中的某节点只有一棵子树,也要区别它是左子树还是右子树(独生子也要称老大!);
2.1 特殊二叉树
另外,二叉树还有特殊的形式:
满二叉树:所有分支节点都存在左子树和右子树,并且所有的叶子都在同一层上。
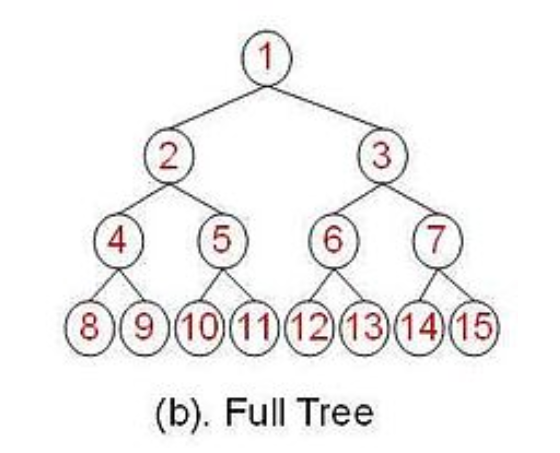
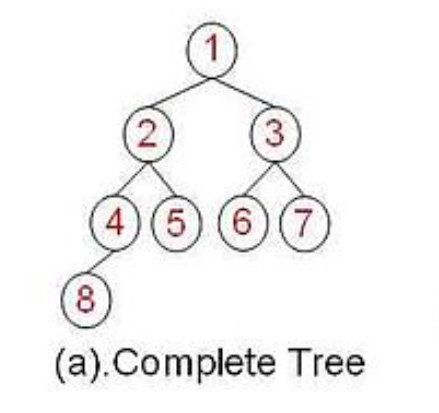
完全二叉树:在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点。
2.2 遍历方式
先序遍历
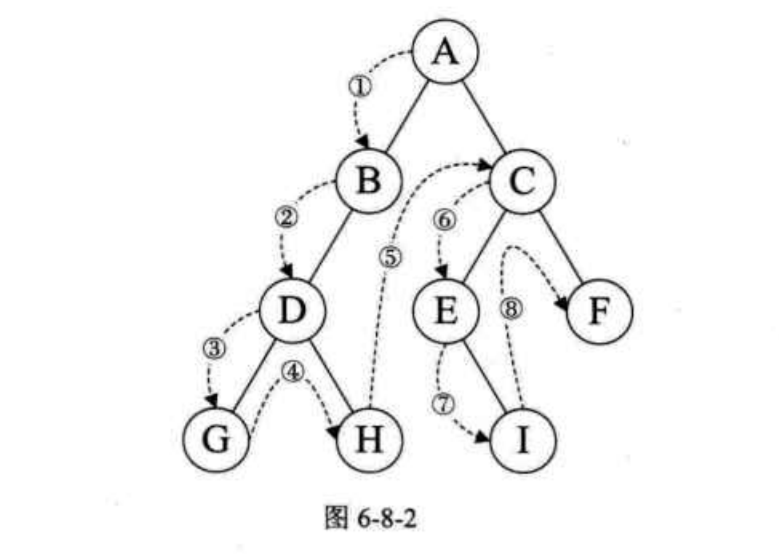
先序遍历的流程是:若二叉树为空, 则空操作返回。否则先访问根节点,然后前序遍历左子树,再前序遍历右子树。遍历的顺序是:A-B-D-G-H-C-E-I-F
中序遍历
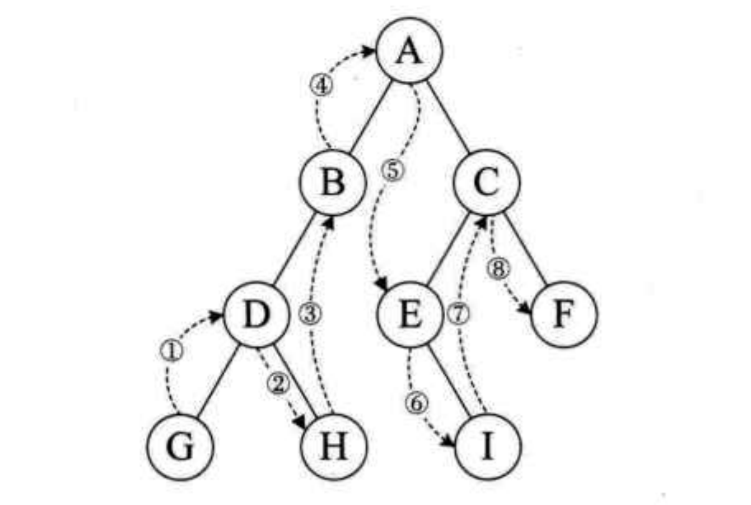
中序遍历的流程是:若树为空,则空操作返回,否则从根节点开始(注意并不是先访问根节点,而是一直找到左子树的叶子),然后中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树。遍历的顺序为:G-D-H-B-A-E-I-C-F。
后序遍历
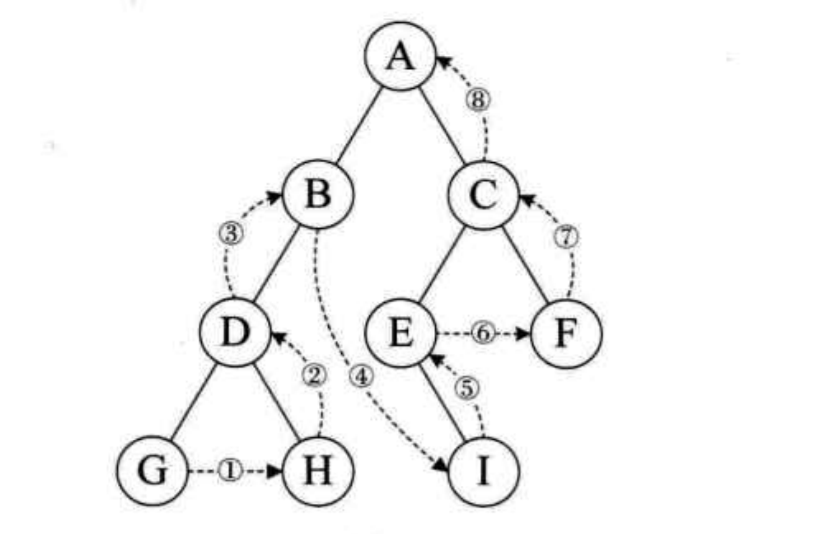
后序遍历的流程是:若树为空, 则空操作为空,否则从左到右先叶子后节点的方式遍历访问左右子树,最后是访问根节点。遍历的顺序为:G-H-D-B-I-E-F-C-A。
3. 编程实现
3.1 C
首先来看C语言的实现,定义结构体BiTNode,表示每个结点的结构体。并定义BiTNode类型的指针变量为BiTree:
typedef struct BiTNode {
int data; // 数据域
struct BiTNode *lChild; // 左子节点
struct BiTNode *rChild; // 右子节点
} BiTNode;
typedef BiTNode* BiTree;
然后定义CreateBiTree,通过先序递归的方法来创建二叉树。当输入的值为-1时代表当前创建的节点无左子节点或者右子节点:
void CreateBiTree(BiTree *T) {
TElementType ch;
scanf("%d", &ch);
if (ch == -1) {
*T = NULL;
return;
}
else
{
*T = (BiTree) malloc(sizeof(BiTNode)); // 申请内存空间,为BiTNode大小
(*T)->data = ch; // 设置数据域的值为输入的值
printf("输入%d的左子节点:",ch);
CreateBiTree(&(*T)->lChild); // 递归调用,构造左子树
printf("输入%d的右子节点:",ch);
CreateBiTree(&(*T)->rChild); // 递归调用,构造右子树
}
}
遍历的方式是从根节点开始遍历,先访问左子节点,该访问左子节点的左子节点,直到访问的左子节点的左子节点为空(T==NULL)。然后依次返回上一次递归调用的地方,开始访问右节点。直到返回到第一次递归调用的地方,开始访问根节点的右子节点,并开始递归调用访问。
因此在遍历的方法中,我们可以反复地递归调用PreOrderTraverse来遍历二叉树的所有子节点:
void PreOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
printf("%d", T->data);
// 递归调用,从根节点的左节点开始遍历
PreOrderTraverse(T->lChild);
PreOrderTraverse(T->rChild);
}
同理,我们可以通过递归的方式来实现中序遍历二叉树:
void InOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
InOrderTraverse(T->lChild);
printf("%d", T->data);
InOrderTraverse(T->rChild);
}
后序遍历也一样:
void PostOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
PostOrderTraverse(T->lChild);
PostOrderTraverse(T->rChild);
printf("%d", T->data);
}
3.2 Java
利用Java面向对象的特点,我们能更简单地实现二叉树的结构。首先定义节点类Node,left和right是对左子节点和右子节点的引用:
static class Node {
public Integer data; // 数据域,当前节点存储的数值
public Node left;
public Node right;
public Node(Integer data) {
this.data = data;
}
}
定义BinaryTree类,提供createTree静态方法进行手动创建根节点,并创建该根节点的左子节点和右子节点,并添加到根节点的引用,最后返回该根节点。
先序递归遍历的方法和C语言实现的差不多:
public class BinaryTree {
/**
* 测试创建二叉树
*/
public static Node createTree() {
Node root = new Node(1);
Node headLeft = new Node(2); // 创建左节点
Node headRight = new Node(3); // 创建右节点
root.left = headLeft; // 添加引用
root.right = headRight;
return root;
}
/**
* 递归实现先序遍历二叉树
*/
public static void preOrderTraverse(Node node) {
if (node == null) {
return;
}
System.out.print(node.data);
preOrderTraverse(node.left);
preOrderTraverse(node.right);
}
}
另外,我们还可以不使用递归,而是使用栈来实现先序遍历二叉树的所有节点。实现的原理是:首先将根节点丢入栈中,每次都取出栈顶节点,如果存在右子节点或者左子节点则放入栈中。需要注意的是,必须是先将右子节点放入栈中,因为先序遍历的话输出的时候左节点优先于右节点输出。
这种遍历的方式称之为深度优先遍历,即从根节点出发,沿着左子树方向进行纵向遍历,直到找到叶子节点为止。然后回溯到前一个节点,进行右子树节点的遍历,直到遍历完所有可达节点为止。
/**
* 深度优先遍历,相当于先序遍历
* 使用栈非递归实现二叉树的遍历
*/
public static void DFS(Node root) {
if (root == null) {
return;
}
Stack<Node> nodes = new Stack<>();
nodes.add(root);
while (!nodes.isEmpty()) {
// 取出栈顶元素,判断是否有子节点
Node temp = nodes.pop();
System.out.println("当前子节点的值: " + temp.data);
if (temp.right != null) {
nodes.push(temp.right);
}
if (temp.left != null) {
nodes.push(temp.left);
}
}
}
如果你听说过深度优先遍历(DFS),那你肯定也知道广度优先遍历(BFS),它是从根节点出发,在横向遍历二叉树层段节点的基础上纵向遍历二叉树的层次。下边我们需要借助队列的数据结构来实现广度优先遍历:
/**
* 广度优先遍历
* 使用队列非递归的方式实现二叉树的遍历
*/
public static void BFS(Node root) {
if (root == null) {
return;
}
Queue<Node> nodes = new ArrayDeque<>();
nodes.add(root);
while (!nodes.isEmpty()) {
Node temp = nodes.remove();
System.out.println("当前的子节点为: " + temp.data);
if (temp.left != null) {
nodes.add(temp.left);
}
if (temp.right != null) {
nodes.add(temp.right);
}
}
}
维基百科上有一张动图能很好地展示出广度优先遍历的过程:

白色代表尚未加入队列且未遍历,灰色代表加入队列等待遍历,黑色则代表已经被遍历。
最后,尽管代码在文中基本给出,但是还是准备了一个小demo。因为我个人看博文的话,如果没有给出一个完整的demo,感觉很难受QAQ...