Coder
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4838 Accepted Submission(s): 1853
Problem Description
In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write
an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done. 1
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
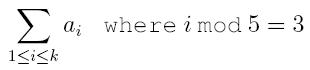
where the set S is written as {a1, a2, ... , ak} satisfying a1 < a2 < a3 < ... < ak
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).
Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.
By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:
1. add x – add the element x to the set;
2. del x – remove the element x from the set;
3. sum – find the digest sum of the set. The digest sum should be understood by
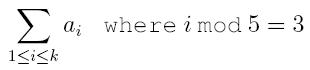
where the set S is written as {a1, a2, ... , ak} satisfying a1 < a2 < a3 < ... < ak
Can you complete this task (and be then fired)?
------------------------------------------------------------------------------
1 See http://uncyclopedia.wikia.com/wiki/Algorithm
Input
There’re several test cases.
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
In each test case, the first line contains one integer N ( 1 <= N <= 105 ), the number of operations to process.
Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.
You may assume that 1 <= x <= 109.
Please see the sample for detailed format.
For any “add x” it is guaranteed that x is not currently in the set just before this operation.
For any “del x” it is guaranteed that x must currently be in the set just before this operation.
Please process until EOF (End Of File).
Output
For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.
Sample Input
9
add 1
add 2
add 3
add 4
add 5
sum
add 6
del 3
sum
6
add 1
add 3
add 5
add 7
add 9
sum
Sample Output
3
4
5
/*
hdu 4288 离线线段树+间隔求和
分别有添加,删除,求和
sum是求 i%5==3的所有数的和,而且数列满足a[0] < a[1] ......
开始以为只会在数列后面添加,然后WR
而且最开始觉得求和很麻烦,于是试了下暴力点的TLE
所以先对所有要用的数进行处理,然后每次找出它们应该在的位置,进行插入删除即可。
主要是没想到两边有规律能推出公式,sum[j]保存当前区间mod 5为j的和
tree[i].sum[j]=(ll)(tree[lson].sum[j]+tree[rson].sum[((j-tree[lson].cnt)%5+5)%5]);
hhh-2016-03-02 23:14:26
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
#include <queue>
#include <vector>
#define lson (i<<1)
#define rson (i<<1|1)
using namespace std;
typedef long long ll;
typedef long double ld;
const int maxn = 500000+10;
int x[maxn];
int tp[maxn],tot;
char opr[maxn][10];
struct node
{
int l,r;
ll sum[6];
int cnt;
int mid()
{
return (l+r)>>1;
}
} tree[maxn<<2];
int flag;
void push_up(int i)
{
for(int j = 0; j < 5; j++)
{
tree[i].sum[j] = (ll)(tree[lson].sum[j]+tree[rson].sum[((j-tree[lson].cnt)%5+5)%5]);
}
}
void build(int i,int l,int r)
{
tree[i].l=l,tree[i].r=r;
tree[i].cnt = 0;
memset(tree[i].sum,0,sizeof(tree[i].sum));
int mid = tree[i].mid();
if(l == r)
return;
build(lson,l,mid);
build(rson,mid+1,r);
}
void update(int i,int k,int val)
{
tree[i].cnt += 2*flag-1;
if(tree[i].l == k && tree[i].r == k)
{
tree[i].sum[0] = flag*val;
return ;
}
int mid = tree[i].mid();
if(k <= mid)update(lson,k,val);
else update(rson,k,val);
push_up(i);
}
int Search(int k)
{
int l = 0,r = tot-1;
while(l<=r)
{
int mid = (l+r)>>1;
if(tp[mid]<k)
l = mid+1;
else if(tp[mid]>k)
r = mid-1;
else
return mid;
}
}
int main()
{
int n;
while(scanf("%d",&n) != EOF)
{
tot = 0;
for(int i = 0; i<n; i++)
{
scanf("%s",opr[i]);
if(opr[i][0] != 's')
{
scanf("%d",&x[i]);
tp[tot++] = x[i];
}
}
sort(tp,tp+tot);
tot = unique(tp,tp+tot)-tp;//去重
if(!tot)
memset(tree[1].sum,0,sizeof(tree[1].sum));
else
build(1,0,tot);
for(int i =0; i < n; i++)
{
if(opr[i][0] == 's')
{
printf("%I64d
",tree[1].sum[2]);
}
else if(opr[i][0] == 'a')
{
flag = 1;
int pos = Search(x[i]);
update(1,pos,x[i]);
}
else if(opr[i][0] == 'd')
{
flag =0 ;
int pos = Search(x[i]);
update(1,pos,x[i]);
}
}
}
return 0;
}