A
-
PZ's solution:
对于斐波那契数列,对于第(n)项,有公式:
[f[n]=f[n-1]+f[n-2] ]作递推处理即可;
-
TAG:递推;斐波那契数列
PZ.cpp
#include<cstdio>
int n;
int main(){
scanf("%d",&n);
long long f1=0,f2=1,f=0;
while(n--){
f=f1+f2;
f1=f2;
f2=f;
}
printf("%lld",f);
return 0;
}
B
-
PZ's solution:
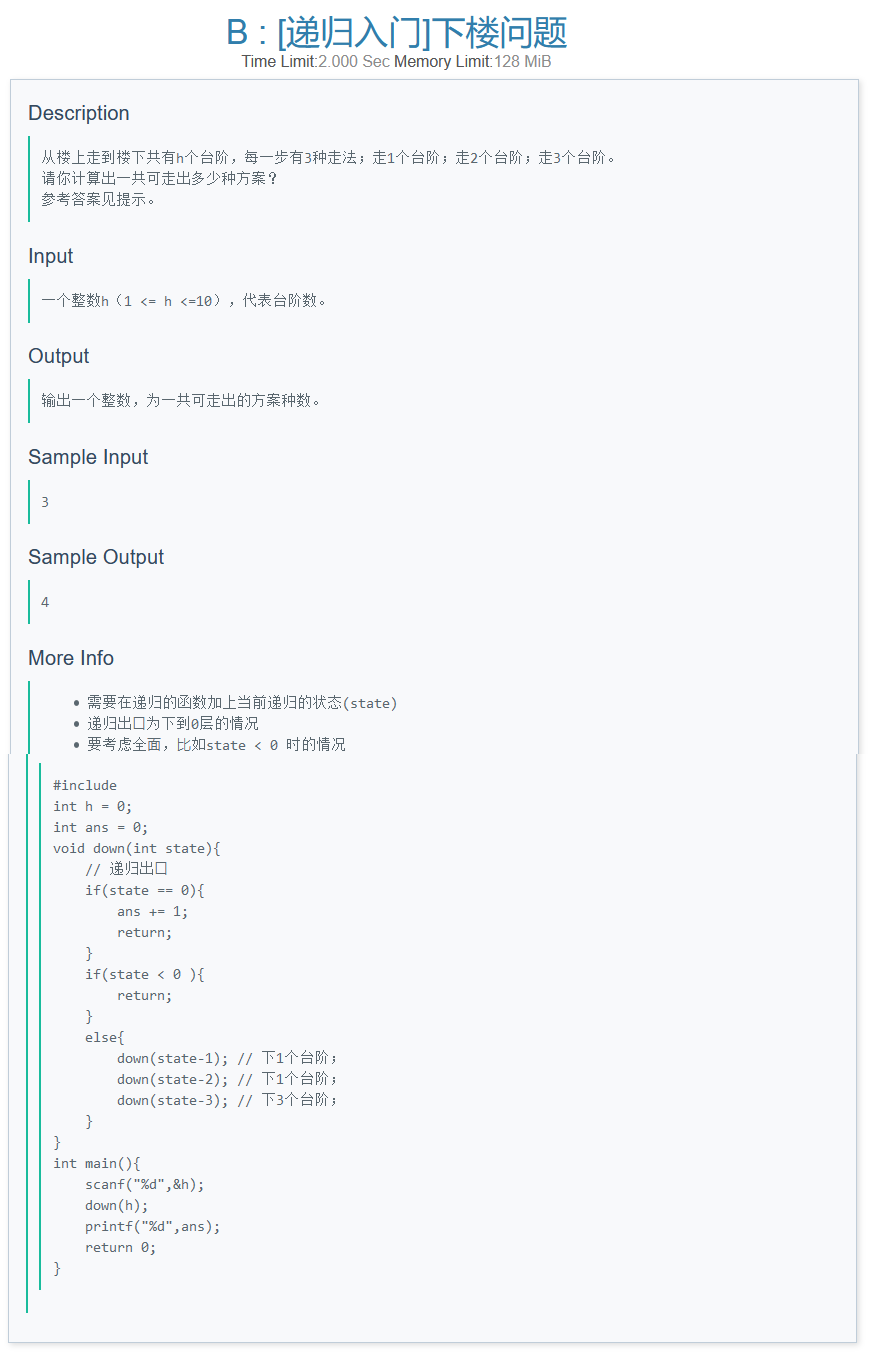
1.DFS递归的代码在More Info中已经展示了,这里使用递推的方法;
2.根据题意,可以处理有0个台阶、1个台阶、2个台阶的情况;
3.对于第(n)阶台阶,它能从第(n-1)、(n-2)、(n-3)阶台阶走上来,那么就有递推式:[f[n]=f[n-1]+f[n-2]+f[n-3] ] -
TAG:递推
PZ.cpp
#include<cstdio>
int n,f[15];
int main(){
scanf("%d",&n);
f[0]=f[1]=1; f[2]=2;
for(int i=3;i<=n;++i)
f[i]=f[i-1]+f[i-2]+f[i-3];
printf("%d",f[n]);
return 0;
}
C
- PZ's solution:
1.对于当前第(n)列方格来说,放置骨牌只有两种情况:
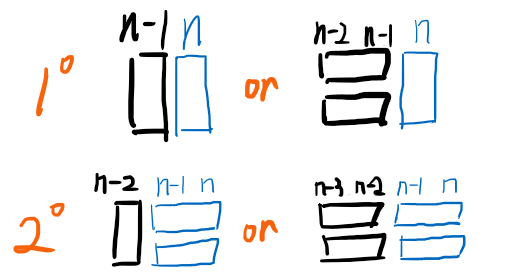
2.对于前面的骨牌如何拜访,是不需要关心的,而当前骨牌的摆放方法总数,取决于第(n-1)列和第(n-2)列骨牌的摆放方法总数,即有递推式:
3.预处理第(1)列和第(2)列的方案数,显然,此为斐波那契数列的递推式;
- TAG:递推;斐波那契数列
PZ.cpp
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define MOD 12345
#define int long long
int n,f[55],cnt=2;
signed main(){
f[1]=1; f[2]=2;
while(scanf("%lld",&n)!=EOF){
if(f[n]){
printf("%lld
",f[n]);
continue;
}
for(int i=cnt+1;i<=n;++i) f[i]=f[i-1]+f[i-2];
cnt=n;
printf("%lld
",f[n]);
}
return 0;
}
D
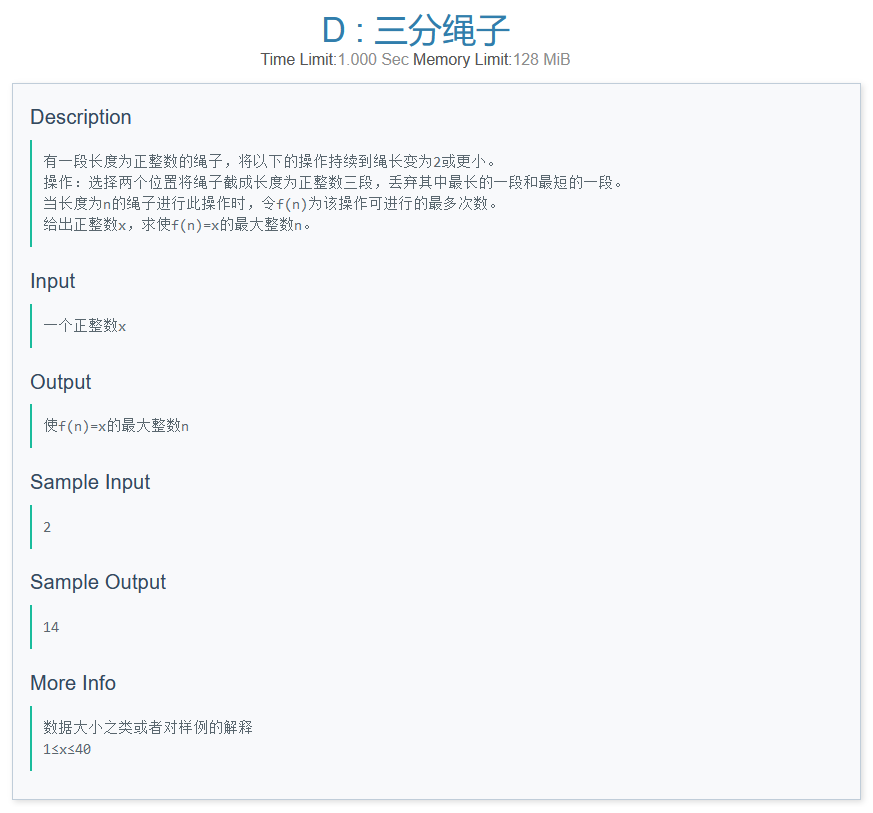
- PZ's solution:
1.对于一段绳子,最优的切法,必然为一段长度为(2),另外两端长度相同(均为最大);
2.此处的最优,即为切后留下的绳子的长度最长的切法;
3.由于绳子长度变为(2)时即不用再切,有(g[0]=2),其中(g(y))表示能进行(y)次操作的绳子的最长长度;
4.由此,有递推式:
- TAG:递推
PZ.cpp
#include<cstdio>
using namespace std;
int x;
long long f[50];
int main(){
scanf("%d",&x);
f[0]=2;
for(int i=1;i<=x;++i) f[i]=f[i-1]*2+2;
printf("%lld",f[x]);
return 0;
}
E
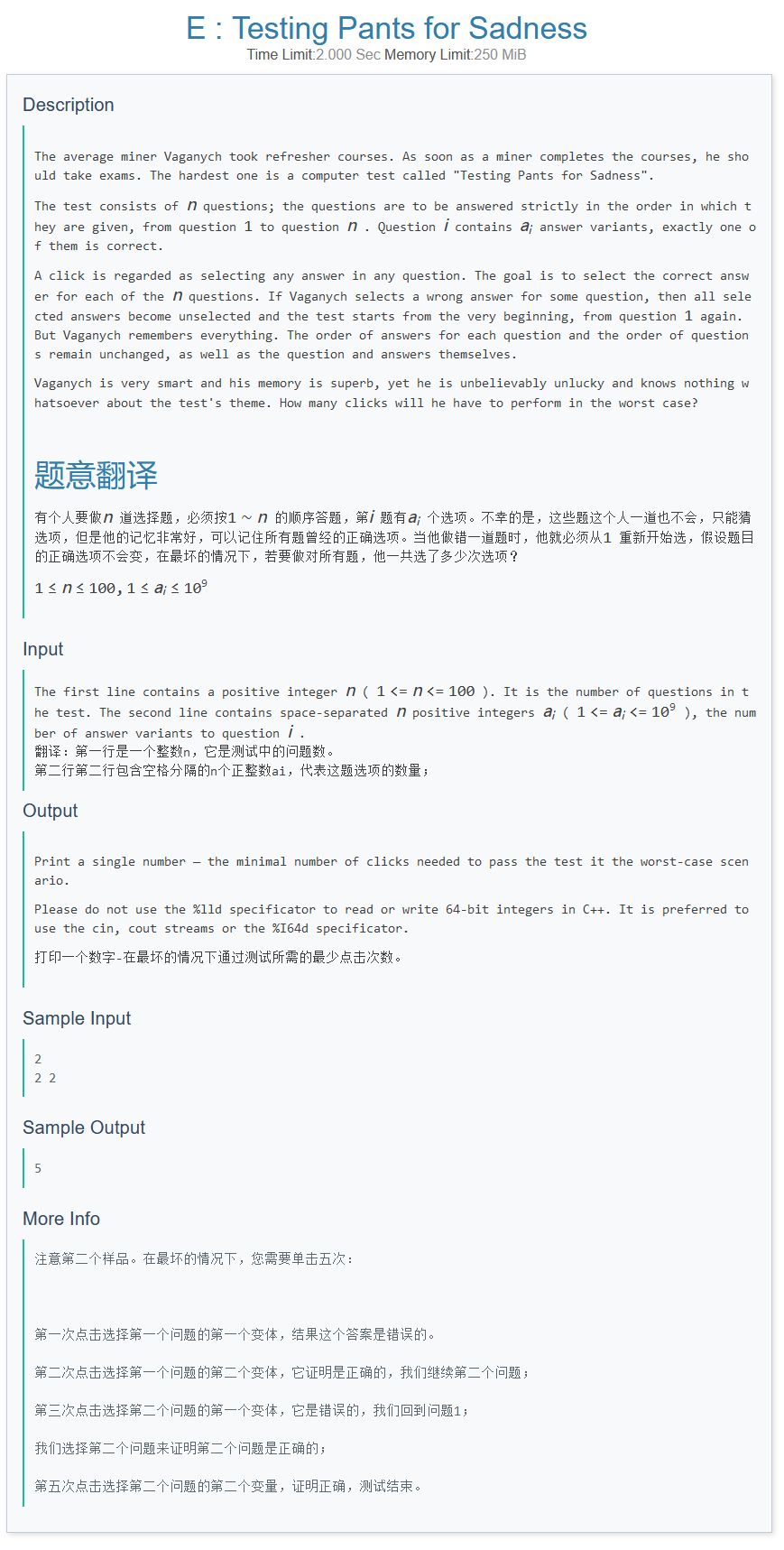
- PZ's solution:
1.对于当前第(n)个问题,假设其有(a_n)个选项,那么最坏情况需要试错(a_n-1)次;
2.每次都需要从头来过,即每个问题对答案的贡献为:
3.进一步解释此式子,如果第(n)个问题只有一个选项,那直接点击((+1))即可,但如果有其他选项,即有(a_n)个选项,则对于后(a_n-1)个选项,每次都需要从头来过,需要再回来点击(n)次,重复(a_n-1)遍,即(n*(a_n-1));
- TAG:递推
PZ.cpp
#include<cstdio>
using namespace std;
#define int long long
int ans,a,n;
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;++i){
scanf("%lld",&a);
ans+=i*(a-1ll)+1ll;
}
printf("%lld",ans);
return 0;
}
F
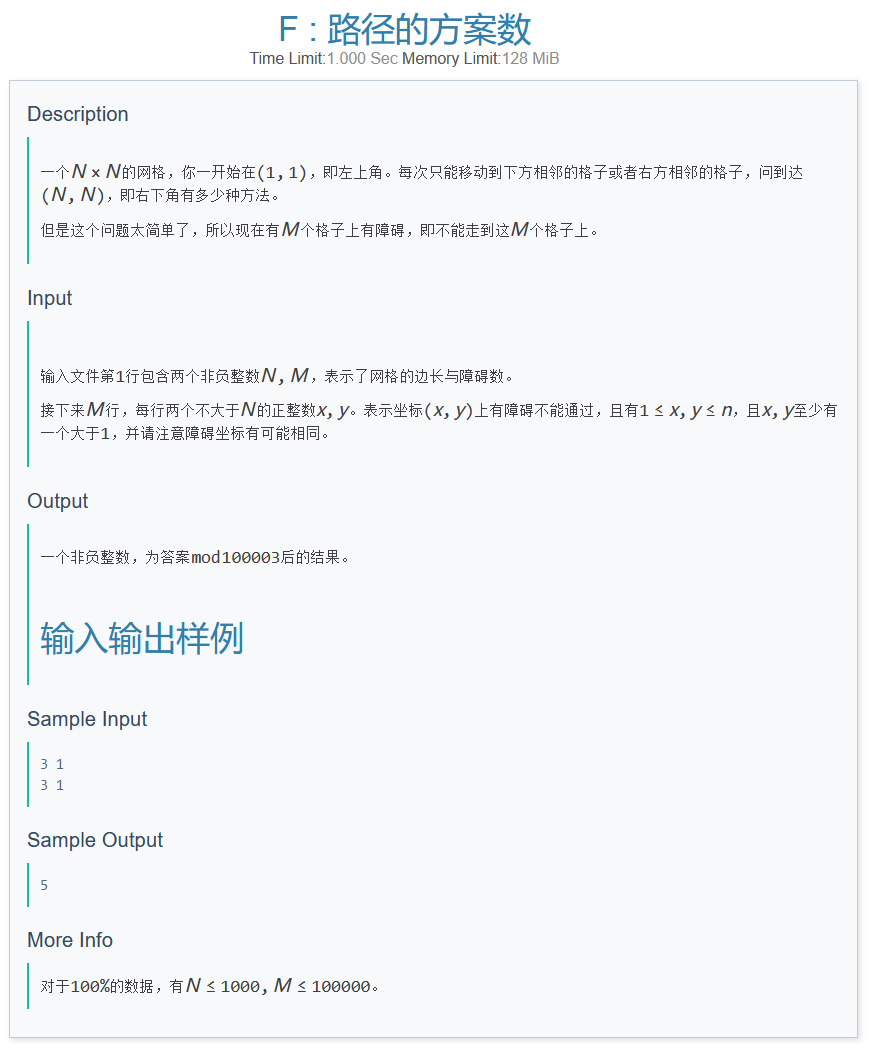
- PZ's solution:
1.根据题意,每次只能移动道下方或右方相邻的格子,换句话说,即对于格子,只能从上方或左方相邻的格子过来,由此可得到递推式:
2.对于障碍物,只需要判断当前点是否可以转移即可,且初始状态为(f[1][1]=1);
- TAG:递推
PZ.cpp
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int n,m,p,f[1005][1005];
bool vis[1005][1005];
int main(){
scanf("%d %d",&n,&m);
for(int x,y,i=1;i<=m;++i){
scanf("%d %d",&x,&y);
vis[x][y]=1;
}
f[1][1]=1;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(!vis[i][j]&&!f[i][j]) f[i][j]=(f[i-1][j]+f[i][j-1])%100003;
printf("%d",f[n][n]);
return 0;
}
G
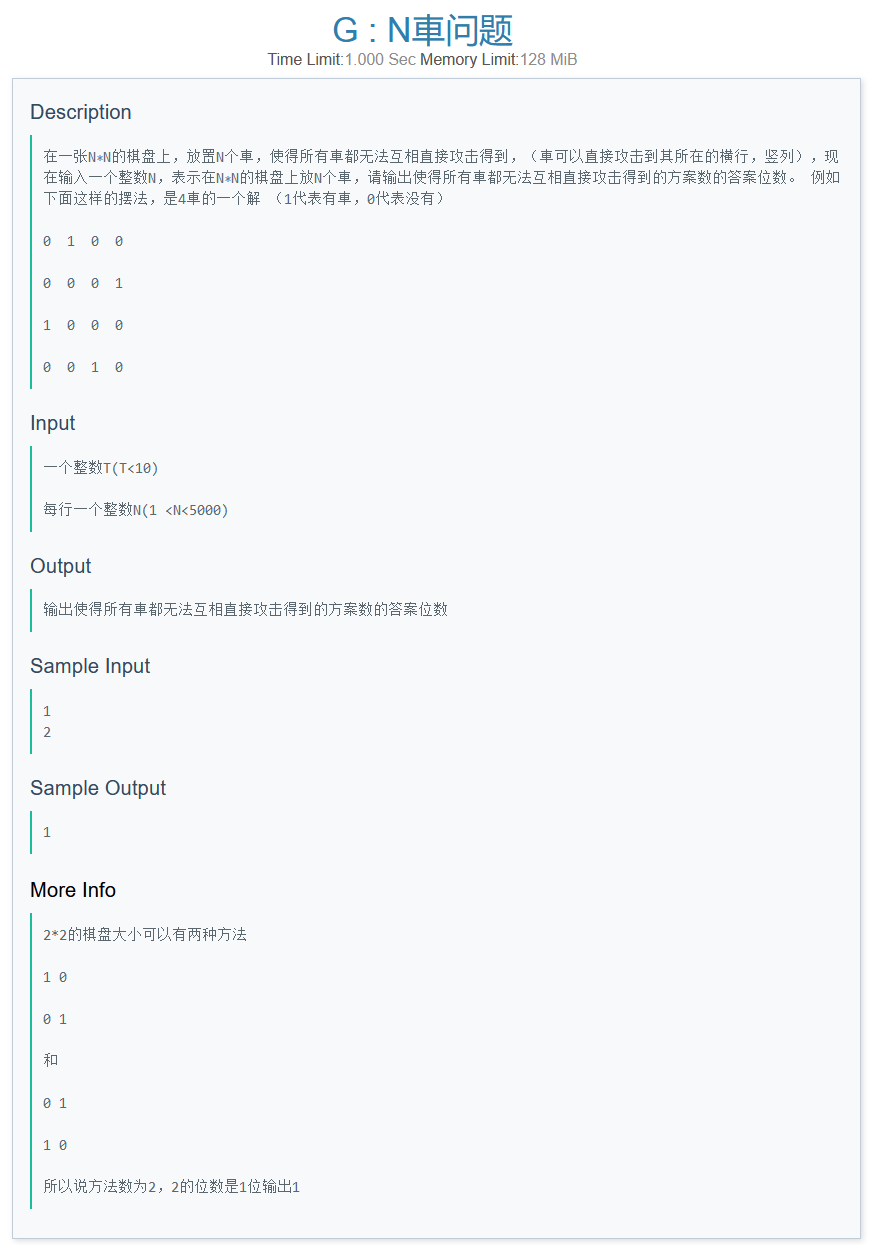
-
Solution:
-
思路借鉴于lhrsdl的n!一共有多少位长度
1.对于题目进行转化,可以发现,将坐标压缩为一维,形成数组(f[n])(对于第(n)列的車,其应放在第几行);
2.可以发现,由于(f[n])中的数互不相同且范围在(1 sim n)内,其实题目求的即为(n)的全排列的数目的位数,对此,有:
3.题目可以转化为求(n!)有多少位
4.根据科学计数法 (x=y*10^z),那么
所以,(n!)的位数即为
因为不光要算出(10^z)的(z),实际上,还有(10^0=1),也就是加一位才是所有位数
- TAG:数学;递推
PZ.cpp
#include<cstdio>
#include<cmath>
using namespace std;
int T,n;
double ans;
int main(){
scanf("%d",&T);
while(T--){
ans=0;
scanf("%d",&n);
for(int i=1;i<=n;++i)
ans+=log10(i);
//log10(x)表示以10为底数,x为真数
printf("%d
",(int)ans+1);
}
return 0;
}
赛后总结
1.本次训练赛的侧重点为递推/递归;
2.观察A题与C题,可以发现,只知道斐波那契数列的通项公式是不够的,C题向我们展示了它的一种应用场景;
3.对于D题,其初始状态并不为(1),这是本题的与众不同之处;
4.对于E题,其无初始状态,且只有一个公式而已,但其也是一种递推的形式;
5.对于F题,其从二维的视角展现了递推,难度虽然次之,但开拓视野意义不小;
6.对于G题,本题相比于C题,更为困难,因为其并非固定的数列的通项公式,而是属于数学的知识点,且题目转换上是需要花费功夫的,也是一道难得一见的开拓视野的题目;
7.本次训练题没有标签到题,因为递推对于未接触编程思想的人来说,还是非常需要理解的事物,它并不像有些题目,不需要独特的编程思想,所以每道题都有很大的思维挑战;
8.递推、动规不分家,但对于这类的题目,总是有遗憾的地方,其在于代码的精短和思维的巧妙,这种题目,可谓是做一道少一道,一旦完全理解一道题背后的思想,那么这道题也就索然无味,所以独立完成、引发思考,是做这些题目必备的态度;