关于DL,由于我是零经验入门,
事实上我是从最简单的ML开始学起,
所以这个系列我也从ML开始讲起。
===============并行分割线=================
一、线性回归
线性回归主要运用于“预测”类问题:
假设我们有一堆的数据(房间大小,房价)。给定一个没见过的房间大小,它的价格应该怎么估计呢?
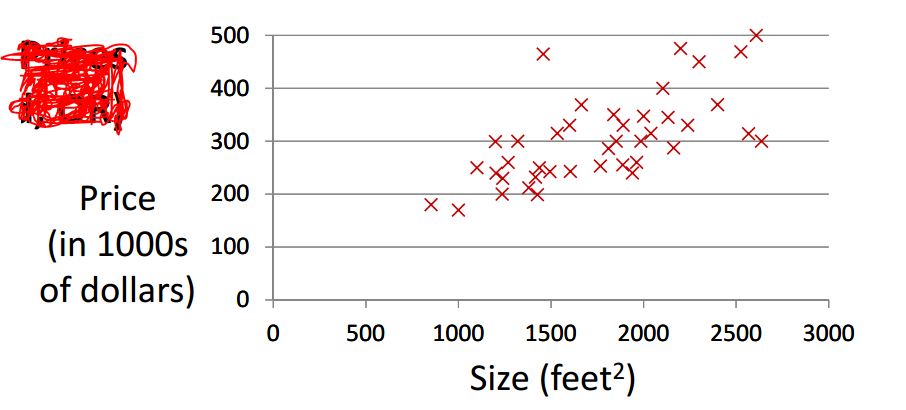
一般来说,我们可以假定房价h(x)和大小x之间存在一种线性关系。求出最优h(x)后,
对于每一个大小x的房间,我们都可以给出一个估价h(x)
概念:COST FUNCTION(代价函数)
给定假设h(x):
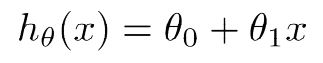
在已知数据的条件下,他的代价函数为J(theta1,theta2):
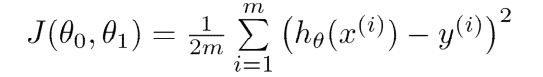
可见,代价函数体现了一种预测值与实际值之间的误差(欧式距离的均值)
而我们的目标——
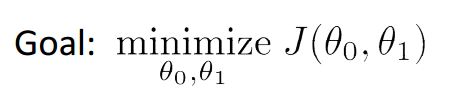
二、Gradient Descent(梯度下降)
梯度下降是一种在已知数据中求解最优h(x)的方法。
核心步骤:
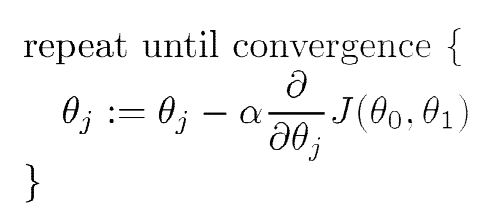
注意:必须在求的所有参数之后同时更新,才能进行下一次循环
原理:
对于一个碗型函数,每进行一次参数更新,都会是取值更加接近最优解(碗底)
以二次函数为例,看起来大概就是这个样子
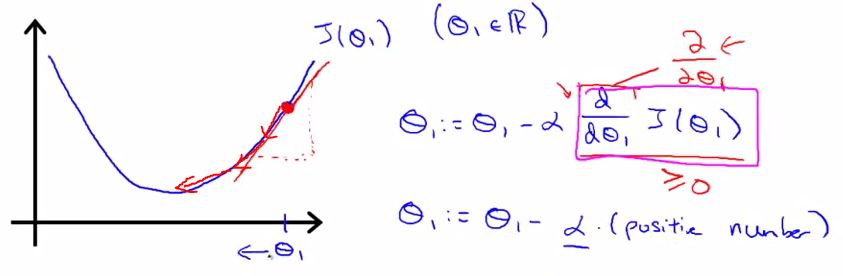
其中alpha称为学习速率(learning rate),过大将会使算法 不能收敛, 过小则收敛过慢
对于有两个参数的单价函数的梯度下降,其收敛过程看起来大概就是这个样子(注意,可以有两种不同路径)
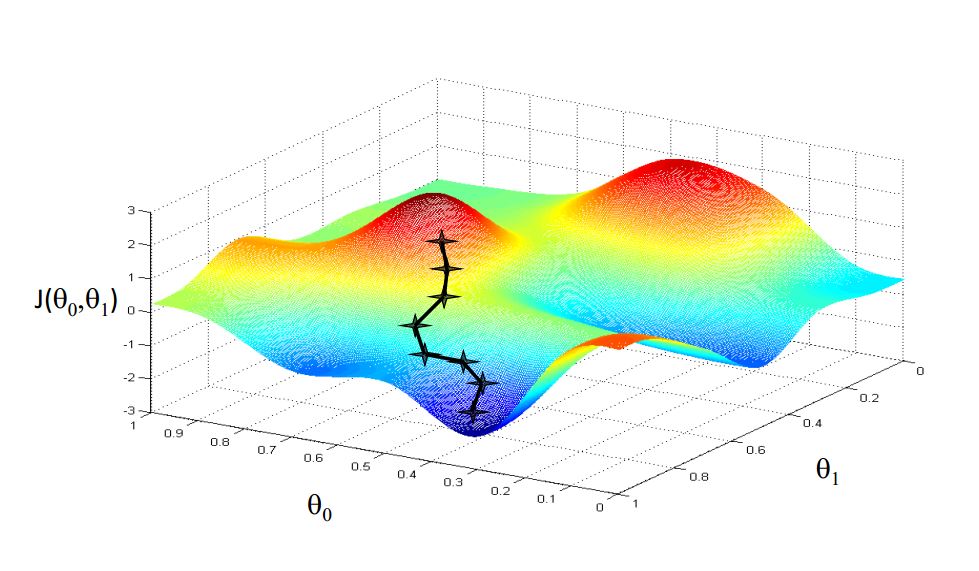
通过不断进行梯度下降,我们可以求得给定数据下的参数的局部最优解
(数学没学好,表述很垃圾,最近准备重学线性代数)
因此,整个线性回归过程可以总结如下:
1、根据给定数据架设预测函数h(x)
2、计算代价函数J
3、计算各参数偏导
4、更新参数
5、重复2~4直到代价函数跟新的步长小于设定值或者是重复次数达到预设值。