后缀数组学习笔记

我是蒟蒻，这个东西机房人均都会了，只有我还不会，只能爬了。

后缀数组的实现

倍增算法

我们可以先比较每一个后缀的第一个字符，然后我们发现在进行下一步比较的时候，就可以利用前一步得到的进行比较了。

这里边体现了倍增的思路，其实放一张比较经典的图就可以明白了：

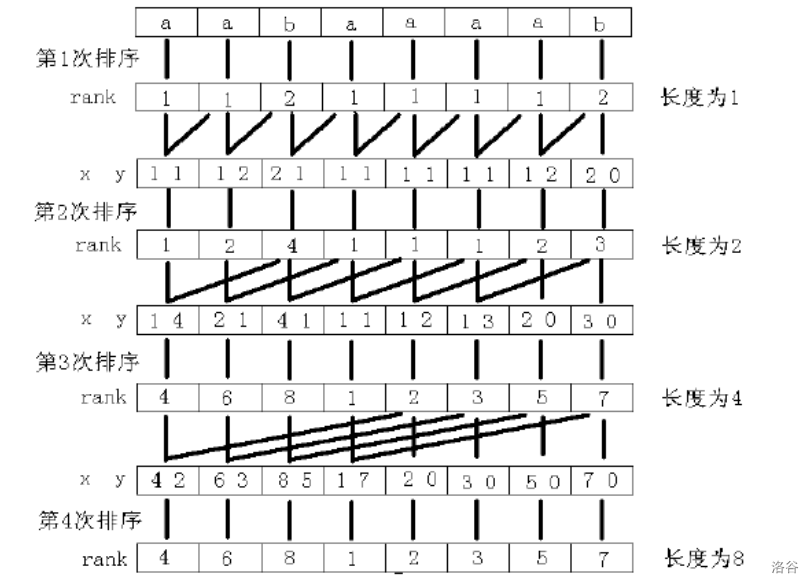
基数排序

我们可以发现，在上述算法的执行过程中，使用的是双关键词排序，这个东西是可以被基数排序优化到 (O(n)) 的。

思路将关键词按重要程度从低到高扔入桶中，再取出来。这样就可以保证在前面的高重要度的关键词相同时，低重要度的相对位置已经正确了。

然后进行两遍即可。

Waring

由于要满足空间复杂度不能过大，所以后缀数组中的基数排序是以一种比较奇怪的方式实现的（在我个人看来），所以下面有两种方案：

1. 自己YY出一种满足时空间复杂度的倍增写法。
2. 全文背诵。

代码如下

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
namespace Suffix_A
{
	int n,m;
	int rk[N],sa[N];
	int buc[N],tp[N];
	void Radix_sort()
	{
		for(int i=1;i<=m;++i) buc[i]=0;
		for(int i=1;i<=n;++i) buc[rk[i]]++;
		for(int i=1;i<=m;++i) buc[i]+=buc[i-1];
		for(int i=n;i>=1;--i) sa[buc[rk[tp[i]]]--]=tp[i];
	}
	void main(char s[])
	{
		n=strlen(s+1),m='z';
		for(int i=1;i<=n;++i) rk[i]=s[i],tp[i]=i;
		Radix_sort();
		for(int len=1;len<=n;len<<=1)
		{
			int tmp=0;
			for(int i=n-len+1;i<=n;++i) tp[++tmp]=i;
			for(int i=1;i<=n;++i) if(sa[i]>len) tp[++tmp]=sa[i]-len;
			Radix_sort();
			swap(rk,tp),tmp=rk[sa[1]]=1;
			for(int i=2;i<=n;++i)
			{
				if(tp[sa[i-1]]==tp[sa[i]]&&tp[sa[i-1]+len]==tp[sa[i]+len])
				rk[sa[i]]=tmp;
				else rk[sa[i]]=++tmp;
			}
			if(n==(m=tmp)) break;
		}
	}
}
int n;
char s[N];
int main()
{
	scanf("%s",s+1);
	n=strlen(s+1);
	Suffix_A::main(s);
	for(int i=1;i<=n;++i) printf("%d ",Suffix_A::sa[i]);
	printf("
");
	return 0;
}

DC3

咕咕咕

SA-IS

咕咕咕

后缀数组的使用

LCP 最长公共前缀

这个东西全称叫做 ( ext{Longest Common Prefix}) 。他在我们的后缀数组中有一些奇妙的性质。

LCP Lemma

[egin{array}{c} ext{LCP}(sa_i,sa_j)=min( ext{LCP}(sa_i,sa_k), ext{LCP}(sa_k,sa_j)) & kin[i,j] end{array} ]

这个东西比较显然，大家自己感性理解一下就可以了。

LCP Theorem

[ ext{LCP}(sa_i,sa_j)=min_{k=i+1}^{j}( ext{LCP}(sa_{k-1},sa_k)) ]

由上面那个东西易得

height 数组的定义

我们设 (ht_i) 表示为已经排好序的第 (s_i) 个串和第 (s_{i-1}) 个串的 ( ext{lcp}) ，即 (ht_i= ext{lcp}(sa_{i-1},sa_i)) ，其中 (ht_1=0) 。

那么由 ( ext{LCP Thoerem}) 可以得到

[ ext{LCP}{sa_i,sa_j}=min_{k=i+1}^j ht_k ]

这样就变成了一个 ( ext{RMQ}) 问题，我们现在的目标就是要快速求出 (ht_i) 。

关于 height 的一个引理

[ht_{rk_i}ge ht_{rk_{i-1}}-1 ]

证明（直接贴一波 ( ext{OI Wiki}) 的）：

求解 height

利用引理暴力求解。

for(int i=1,len=0;i<=n;++i)
{
	if(len) len--;
	while(s[i+len]==s[sa[rk[i]-1]+len]) len++;
	ht[rk[i]]=len;
}

height 的应用

求 LCP

就是前面说的，转化为 ( ext{RMQ}) 问题。

比较子串的大小关系

若需要比较的是 (A=S[a...b]) 和 (B=s[c...d]) 。

若 ( ext{LCP}(a,c)ge min(|A|,|b|)) ，则 (A<BLongleftrightarrow |A|<|B|)

否则，(A<BLongleftrightarrow rk_a<rk_c)

不同子串的数目

转化到 ( ext{SA}) 上就是求不同前缀的个数。

所以答案易得为：

[ans=frac{n(n+1)}{2}-sum_{i=2}^n height_i ]

出现至少 k 次的子串的最大长度

出现至少 (k) 次意味着后缀数组中有至少连续 (k) 个后缀的 ( ext{LCP}) 是这玩意。

求出每相邻 (k-1) 个 (height) 的最小值，再在最小值中求最大值即可。

出现至少 k 次的不重叠的子串的最大长度

出这个应用纯粹是模拟赛里的毒瘤题。。。（好吧，对于字符串的神们来说这根本不毒瘤。

(Link)

参考文章

后缀数组 (SA)——( ext{OI Wiki})

浅谈后缀数组算法——( ext{blackfrog})

其他字符串算法学习笔记（不定期更新）——( ext{Flying2018})