看了下题解,感觉有点弄懂了,但是好像还是不是很清楚,打算一边写草稿,一边写题,一边写题解,用以加深印象。
题目大意
就是你有一颗表示区间 ([1,n]) 的线段树。一开始树上的 (tag) 均为 (0) 。你接下来会进行 (m) 次操作。
1 l r:假设当前手上有 (t) 棵线段树,你需要会把每棵线段树复制两份( (tag) 数组也一起复制),原先编号为 (i) 的线段树复制得到的两棵编号为 (2i-1) 与 (2i) ,在复制结束后,一共有 (2t) 棵线段树。接着,你需要会对所有编号为奇数的线段树进行一次 (operatorname{Modify}(root,1,n,l,r)) 。
其中 (operatorname{Modify}) 操作的函数如下:

2:定义一棵线段树的权值为它上面有多少个节点 (tag) 为 (1)。输出所有线段树的权值和。
草稿 和 题解
有一个非常 (naive) 的做法,就是每一次暴力复制线段树,然后进行相应的操作,但是我们发现这个方法最多只能跑 (m=10) ,非常不可行。
然后我们考虑这个复制线段树的操作意义在于何?他无非是求对于到当前操作选或者不选的所有方案中, (tag) 的数量和,这个对于我们来说就是变着法的计数,我们考虑 ( ext{dp}) 。
首先我们考虑状态的设计,我们发现,对于当前已经有的线段树中,同一个节点的操作是可以一起看的,因为我们只需要知道最后的和而并不需要其中具体的值,所以我们不妨设 (f_{i,j}) 表示节点 (i) 到第 (j) 个操作的时候,他的数量和是多少,那么对于不同的点,他的处理方式不一样。
我打算 (he) 一下题解的图(不代表着我在一边看题解一边写题啊……),就用神 ( ext{Sooke}) 的吧:
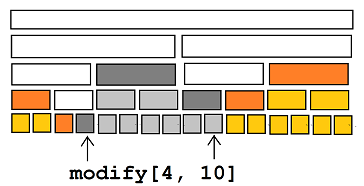
可以发现,对于一次 (operatorname{Modify}) ,整个线段树的点只会有 (5) 种情况,我们可以分开讨论:
-
对于白色点,即是会被执行 (operatorname{Pushdown}) 的点,是不会将这个 (tag) 标记在这里最后留下,因为他会将其传递到自己的下方 。
-
对于黑色点,即是你最终打 (tag) 的点。
-
对于橙色点,是需要接受 (tag) 的点,但是不需要打 (tag) 。
-
对于黄色点和灰色点,都是在这一次操作过程中不需要变动的点,我们只需要将其的 (f) 数组乘以 (2) 即可。
对于上述的操作,我们发现,我们还需要找出这个点上方有多少 (tag) 要继承。这个东西也需要维护,因为我们发现我们不能在修改的时候直接得出。我们不妨设 (g_{i,j}) 表示节点 (i) 到第 (j) 个操作时,有多少棵线段树在 (i) 点及 (i) 点上方的节点中有 (tag) 。同样的,对于这个东西的维护,对于不同的节点也是不一样的。
-
对于白色点,我们发现这个东西在进行操作的那一半线段树中是会被清零的,因为他们节点的 (tag) 会全部下放。
-
对于黑色点和灰色点,由于其自己或上方的点必定会打上 (tag) ,所以 (g) 的增量就是线段树个数的增量,即 (2^j) 。
-
对于黄色点和橙色点,由于并没有加 (tag) 或进行下传 ,同时其上方的点的 (tag) 也不会有变,所以说对于他来说,自己的 (g) 并没有变化,乘以 (2) 即可。
然后发现我们就可以维护了。
如果直接判断点的颜色再进行相应的操作是 (O(n^2)) 的,时间还是不满足,所以我们考虑在线段树上维护 ( ext{dp}) 。然后应该就可以做了。具体的操作方式可以看代码,虽然还没写完。
代码如下
#include<bits/stdc++.h>
using namespace std;
#define Lint long long
const int N=1e5+5,M=1e5+5;
const Lint MOD=998244353;
int n,m,cnt=0;
Lint ksm[M];
struct Seg_Tree
{
struct Node{Lint sum,f,g,tagf,tagg1,tagg2;}tr[N<<2];
void build(int u,int l,int r)
{
tr[u].f=tr[u].g=tr[u].sum=0;
tr[u].tagf=tr[u].tagg1=1,tr[u].tagg2=0;
if(l==r) return ;
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
}
void up(int u){tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum+tr[u].f)%MOD;}
void updataf(int u,Lint z)
{
tr[u].f=(tr[u].f*z)%MOD;
tr[u].sum=(tr[u].sum*z)%MOD;
tr[u].tagf=(tr[u].tagf*z)%MOD;
}
void updatag(int u,Lint z1,Lint z2)
{
tr[u].g=(tr[u].g*z1%MOD+z2)%MOD;
tr[u].tagg1=tr[u].tagg1*z1%MOD;
tr[u].tagg2=(tr[u].tagg2*z1%MOD+z2)%MOD;
}
void down(int u)
{
updataf(u<<1,tr[u].tagf);
updataf(u<<1|1,tr[u].tagf);
tr[u].tagf=1;
updatag(u<<1,tr[u].tagg1,tr[u].tagg2);
updatag(u<<1|1,tr[u].tagg1,tr[u].tagg2);
tr[u].tagg1=1,tr[u].tagg2=0;
}
void opt(int u,int l,int r,int x,int y,int now)
{
if(x<=l&&r<=y)
{
tr[u].sum=(tr[u].sum+MOD-tr[u].f)%MOD;
tr[u].f=(tr[u].f+ksm[now-1])%MOD;
tr[u].sum=(tr[u].sum+tr[u].f)%MOD;
updatag(u,1,ksm[now-1]);//black
if(l!=r)
{
down(u);
updataf(u<<1,2);
updataf(u<<1|1,2);//grey
up(u);
}
return ;
}
int mid=(l+r)>>1;
down(u);//white
if(x<=mid) opt(u<<1,l,mid,x,y,now);
else
{
tr[u<<1].sum=(tr[u<<1].sum+MOD-tr[u<<1].f)%MOD;
tr[u<<1].f=(tr[u<<1].f+tr[u<<1].g)%MOD;
tr[u<<1].sum=(tr[u<<1].sum+tr[u<<1].f)%MOD;//orange
if(l!=mid)
{
down(u<<1);
updataf(u<<2,2);
updataf(u<<2|1,2);//yellow
up(u<<1);
}
updatag(u<<1,2,0);//orange and yellow
}
if(y>mid) opt(u<<1|1,mid+1,r,x,y,now);
else
{
tr[u<<1|1].sum=(tr[u<<1|1].sum+MOD-tr[u<<1|1].f)%MOD;
tr[u<<1|1].f=(tr[u<<1|1].f+tr[u<<1|1].g)%MOD;
tr[u<<1|1].sum=(tr[u<<1|1].sum+tr[u<<1|1].f)%MOD;//orange
if(mid+1!=r)
{
down(u<<1|1);
updataf((u<<1|1)<<1,2);
updataf((u<<1|1)<<1|1,2);//yellow
up(u<<1|1);
}
updatag(u<<1|1,2,0);//orange and yellow
}
up(u);
}
}t;
int main()
{
cin>>n>>m,ksm[0]=1;
for(int i=1;i<=m;++i) ksm[i]=(ksm[i-1]<<1)%MOD;
t.build(1,1,n);
while(m--)
{
int opt,x,y;
scanf("%d",&opt);
if(opt==1)
{
scanf("%d%d",&x,&y);
t.opt(1,1,n,x,y,++cnt);
}
else printf("%lld
",t.tr[1].sum);
}
return 0;
}