问题 C: 最短路径

问题 C: 最短路径

在洛谷上刷最短路的题然后被老师拉回去做算法笔记上面的题。。。

拿到这道题，先确定所有路径唯一，然后是无向边，那么对于边权处理，直接赋值为2的k次方就可以了，然后直接跑最短路。

这种思路非常暴力，但仔细看题目的数据范围，k<=500，ull你估计都存不下，没救。有的同学可能会想，反正最后都要mod 1e5，那我在存储的时候mod就行了嘛，很多题都可以这样。但是对于最短路，你明显不可能这么跑，看下面这个例子

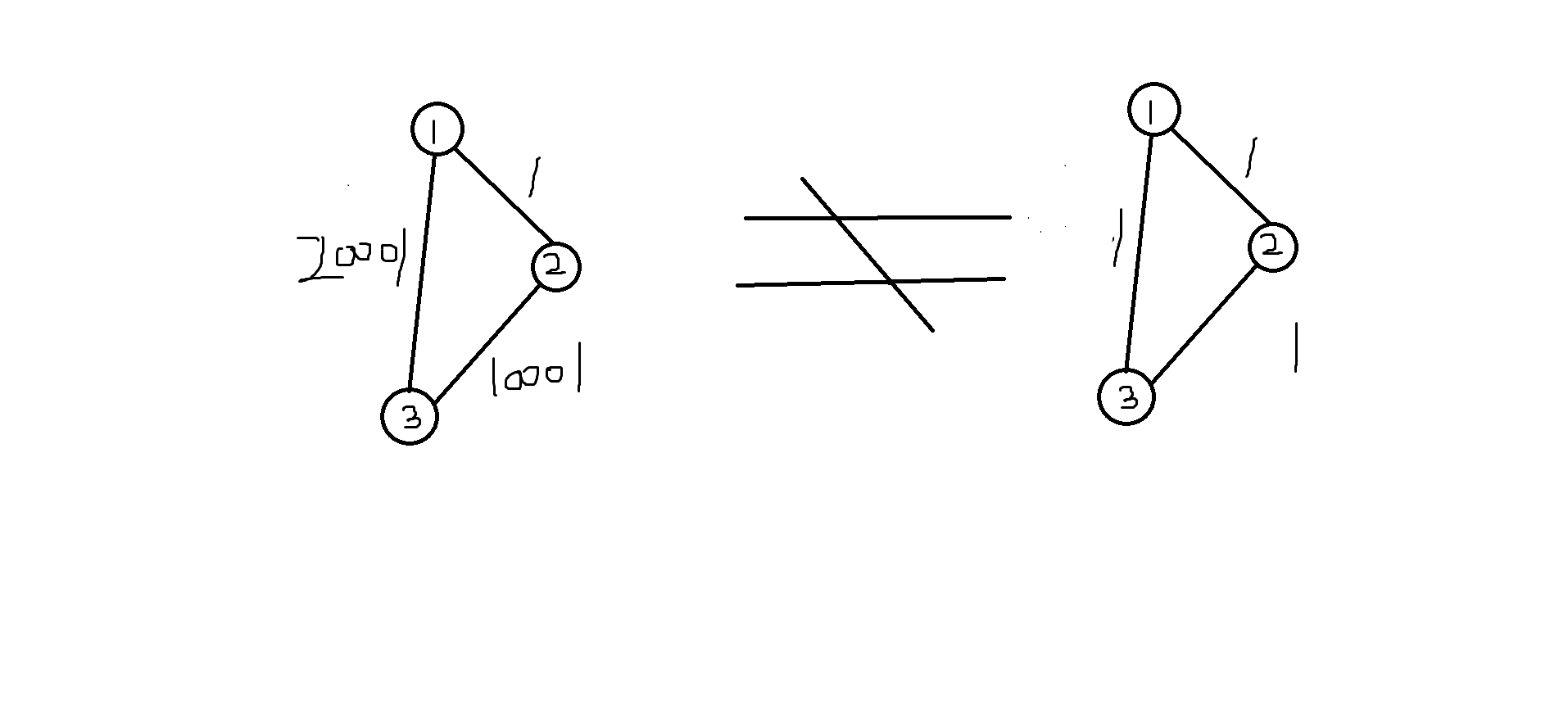
显然，你处理之后肯定会出错，那你就要换个思想了。如果你把边权2^k直接存储为k会怎么样呢？如果再进行一次最小生成树，最终处理的结果和跑最短路的答案其实是一样的（如图）

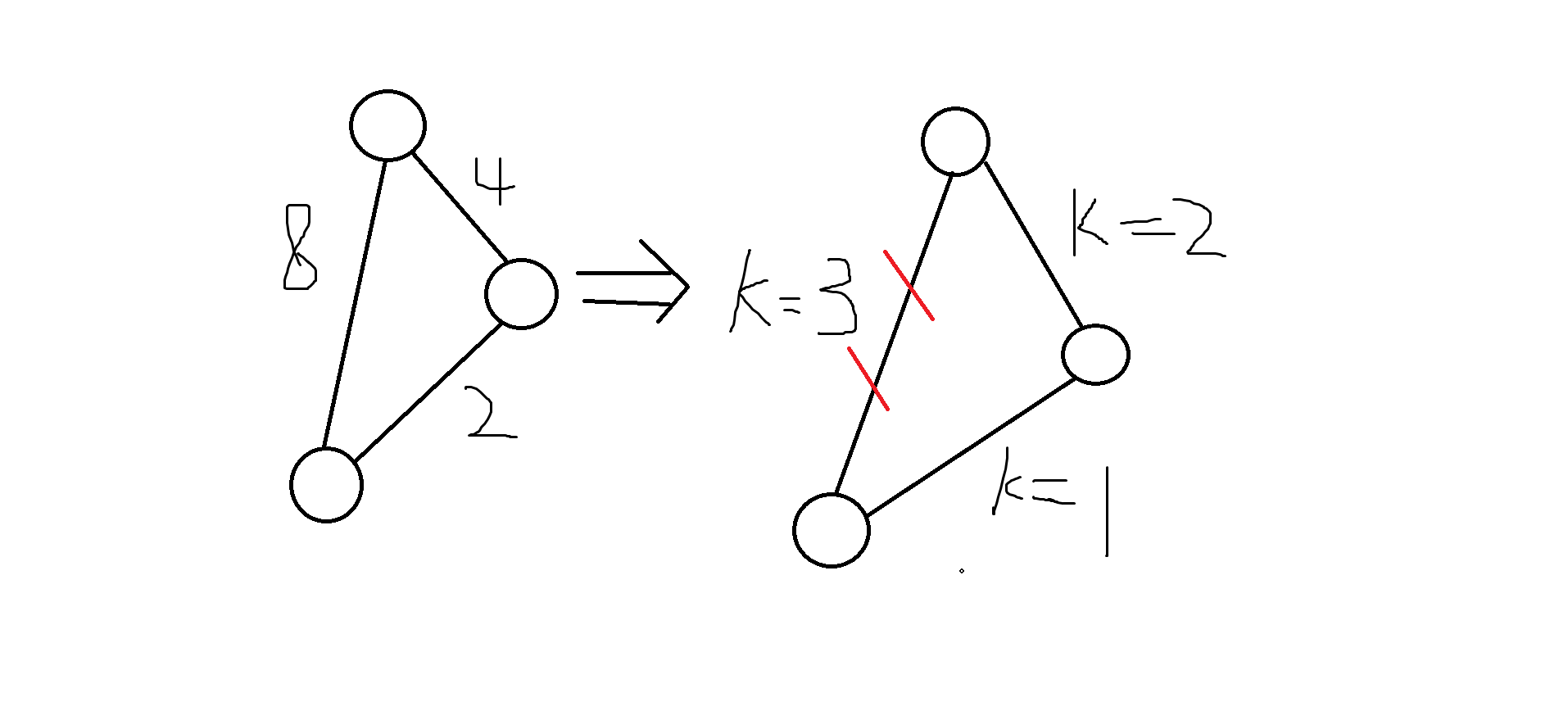
这样来想，这道题就迎刃而解了，在处理好最小生成树之后，我们知道出发点，然后DFS一遍整颗树，处理出每一个边权，记住有可能会有孤儿城市，与其他城市不连通，特判为-1

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+50;
const int mod=100000;
int f[MAXN];
int n,m;
int po[505];
struct edge {
    int to,net,v;
} ee[MAXN]; //链式前向星 
int head[MAXN];
int find(int x) {
    if(f[x]==x) return x;
    return f[x]=find(f[x]);
}
void merge(int x,int y) {
    f[find(x)]=find(y);
}//并查集标准操作 
int tot;
void add(int u,int v,int w) {
    ee[++tot].net=head[u];
    ee[tot].to=v;
    ee[tot].v=w;
    head[u]=tot;
}//建边 
int ans[MAXN];
bool vis[MAXN];
void dfs(int s) {
    vis[s]=1; //已经走过这个点 
    for(register int i=head[s]; i; i=ee[i].net)
        if(!vis[ee[i].to]) { //如果没有走过 
            ans[ee[i].to]=(ans[s]%mod+po[ee[i].v])%mod; //当前节点的距离是父亲节点的距离+当前的权值 
            dfs(ee[i].to); //继续找儿子节点 
        }
}
int main() {
    po[0]=1;
    for(register int i=1;i<500;i++) po[i]=po[i-1]%mod*2%mod;  //预处理2的幂 
    while(scanf("%d%d",&n,&m)!=EOF) {
        memset(ans,0,sizeof ans);
        memset(ee,0,sizeof ee);
        memset(f,0,sizeof f);
        memset(vis,false,sizeof vis);
        memset(head,0,sizeof head);
        tot=0;  //多组数据一定记得清空数组和变量 
        for(register int i=0; i<n; i++) f[i]=i; //并查集初始化 
        for(register int i=1; i<=m; i++) { //最小生成树的实现 
            int u,v;
            scanf("%d%d",&u,&v);
            int x=find(u),y=find(v);
            if(x!=y) { //如果不在一个集合 
                add(u,v,i-1); 
                add(v,u,i-1); //建双向变 
                merge(x,y); //合并 
            } //标准的Kruskal 
        }
        dfs(0); //dfs找路的长度 
        for(register int i=1; i<n; i++) {
            if(vis[i]!=0) {
                cout<<ans[i]%mod<<endl;
            } else cout<<-1<<endl; //处理答案，如果没被访问过，说明是孤儿 
        }
    }
    return 0;
}