C++ 数据结构 4：排序

1 基本概念

1.1 定义

排序是计算机内经常进行的一种操作，其目的是将一组“无序”的数据元素调整为“有序”的数据元素。

1.2 数学定义

假设含n个数据元素的序列为 { R1, R2, …, Rn}，其相应的关键字序列为 { K1, K2, …, Kn} 这些关键字相互之间可以进行比较，即在它们之间存在着这样一个关系 ： Kp1≤Kp2≤…≤Kpn

按此固有关系将上式记录序列重新排列为 { Rp1, Rp2, …，Rpn} 的操作称作 排序。

1.3 排序的稳定性

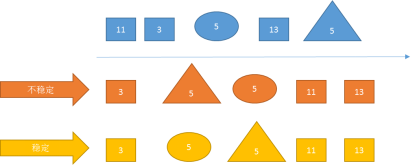
如果在序列中有两个数据元素 r[i] 和 r[j]，它们的关键字 k[i] == k [j]，且在排序之前，对象 r[i] 排在 r[j] 前面。如果在排序之后，对象 r[i] 仍在 r[j] 前面，则称这个排序方法是稳定的，否则称这个排序方法是不稳定的。

1.4 排序中的关键操作

• 比较：任意两个数据元素通过比较操作确定先后次序

• 交换：数据元素之间需要交换才能得到预期结果

1.5 内排序和外排序

• 内排序：整个排序过程不需要访问外存便能完成

• 外排序：待排序的数据元素数量很大，整个序列的排序过程不可能在内存中完成

1.6 总结

• 排序是数据元素从无序到有序的过程

• 排序具有稳定性，是选择排序算法的因素之一

• 比较和交换是排序的基本操作

• 多关键字排序与单关键字排序无本质区别

• 排序的时间性能是区分排序算法好坏的主要因素

2 选择排序

2.1 算法介绍

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素拍完。

2.2 基本思想

设数组为 a[0] ~ a[n-1]

1. 初始时，数组全为无序区为 a[0] ~ a[n-1]，令 i = 0

2. 在无序区 a[i] ~ a[n-1] 中选取一个最小的元素，将其与 a[i] 交换，交换后 a[0] ~ a[i] 就形成了一个有序区

3. i++ 并 重复第 2 步，直到 i == n-1，排序完成。

简单来说：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2.3 算法实现

#include <stdio.h>
#include <stdlib.h>

//选择排序(升序排列)
void selectionSort(int *array, int len)
{
	int min = 0;	// 指向最小的元素的位置

	int i = -1;
	int j = -1;
	int k = -1;

	// 外层循环
	for (i = 0; i < len - 1; ++i)
	{
		min = i;

		// 内存循环
		for (j = i + 1; j < len; ++j)
		{
			// 判断
			if (array[min] > array[j])
			{
				// 保存最小的元素的位置
				min = j;
			}
		}

		// 判断是否需要交换
		if (min != i)
		{
			// 找到了新的最小值

			// 交换
			int tmp = array[min];

			array[min] = array[i];

			array[i] = tmp;
		}


		printf("第 i =  %d 次，排序后的数组为：
",i);

		for (k = 0; k < len; ++k)
		{
			printf("%d	", array[k]);
		}

		printf("
");
	}
}

#if 1
void main()
{
	int i;

	//定义整型数组
	int array[] = { 12, 5, 33, 6, 10 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	//排序
	selectionSort(array, len);

	//遍历
	printf("选择排序之后的序列:	");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

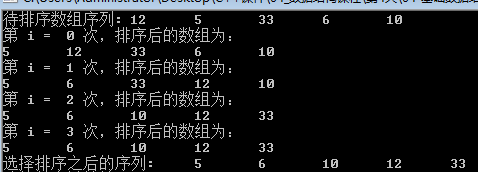
运行结果：

2.4 稳定性

• 选择排序是不稳定的排序方法

• 选择排序效率：(O（n^2）)

3 冒泡排序

3.1 算法介绍

冒泡排序算法的运作如下：

从后往前

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

3. 针对所有的元素重复以上的步骤，除了最后一个。

4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

3.2 基本思想

设数组长度为 N。

从后往前

1. 比较相邻的前后两个数据，如果 前面数据大于后面的数据，就将两个数据交换

2. 这样对数组的第 0 个数据到 N-1 个数据进行一次遍历后，最大的一个数据就“升”到数组第 N-1 个位置

3. N = N-1，如果 N 不为 0 就重复前面两步，否则排序完成。

3.3 排序过程

3.4 算法实现

#include <stdio.h>
#include <stdlib.h>

//冒泡排序(升序)
void bubbleSort(int *array, int len)	
{
	int i = -1;
	int j = -1;
	int k = -1;

	// 判断数组是否已排序好 0: 没有排好, 1: 已经排好
	int flag = 0;

	int tmp = -1;

	for (i = len - 1; i > 0 && flag == 0; --i)
	{
		flag = 1;	// 假设已经排序好

		for (j = 0; j < i; ++j)
		{
			if (array[j] > array[j + 1])
			{
				tmp = array[j];
				array[j] = array[j + 1];
				array[j + 1] = tmp;

				flag = 0;	// 此段代码被执行，说明还没有排好
			}
		}

		printf("i =  %d ，排序后的数组为：
",i);

		for (k = 0; k < len; ++k)
		{
			printf("%d	", array[k]);
		}

		printf("
");
	}
}

#if 1
void main()
{
	int i;

	//定义整型数组
	int array[] = { 11, 8, 7, 6, 3 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	//排序
	bubbleSort(array, len);

	//遍历
	printf("冒泡排序之后的序列:	");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

运行结果：

3.5 冒泡总结

• 冒泡排序是一种效率低下的排序方法，在数据规模很小时，可以采用。数据规模比较大时，最好用其它排序方法。

• 上述例子总对冒泡做了优化，添加了exchange作为标记，记录序列是否已经有序，减少循环次数。

3.6 稳定性

• 冒泡排序是一种稳定的排序算法

• 冒泡排序的效率：(O（n^2）)

4 插入排序

4.1 算法介绍

每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

4.2 基本思想

设数组为 a[0] ~ a[n-1]

1. 初始时，a[0] 自成 1 个有序区，无序区为 a[1] ~ a[n-1]。令 i = 1

2. 将 a[i] 并入当前的有序区 a[1] ~ a[i-1] 中形成 a[0] ~ a[i] 的有序区间。

3. i++ 并重复第 2 步直到 i == n-1 。排序完成。

4.3 算法实现

#include <stdio.h>
#include <stdlib.h>

//插入排序算法(升序排列)
void insertionSort(int *array, int len)
{
	int tmp = 0;	// 存储基准数
	int index = 0;	// 坑的位置

	int i = -1;
	int j = -1;
	int k = -1;

	// 遍历无序序列
	for (i = 1; i < len; ++i)
	{
		index = i;
		tmp = array[i];

		// 遍历有序序列(从后往前)
		for (j = i - 1; j >= 0; --j)
		{
			// 基准数根有序序列中的元素比较
			if (tmp < array[j])
			{
				// 有序序列元素后移
				array[j + 1] = array[j];
				// 坑的位置
				index = j;
			}
			else
			{
				break;
			}
		}
		// 填坑
		array[index] = tmp;

		printf("i =  %d ，排序后的数组为：
",i);

		for (k = 0; k < len; ++k)
		{
			printf("%d	", array[k]);
		}

		printf("
");
	}
}

#if 1
void main()
{
	int i = -1;

	//定义整型数组
	int array[] = { 12, 5, 33, 6, 10 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	//排序
	insertionSort(array, len);

	//遍历
	printf("插入排序之后的序列:");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

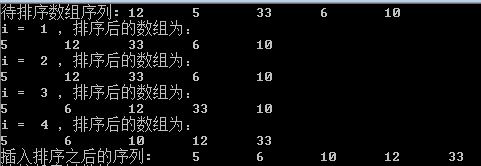
运行结果：

4.4 稳定性

• 插入排序是稳定的排序算法

• 插入排序效率：(O（n^2）)

5 希尔排序

5.1 算法介绍

希尔排序的实质就是分组插入排序，该方法又称缩小增量排序，因 DL．Shell 于 1959 年提出而得名。

5.2 基本思想

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

简单来说：

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个数组恰被分成一组，算法便终止。

5.3 排序过程

5.4 算法实现

#include <stdio.h>
#include <stdlib.h>

//希尔排序
void shellSort(int *array, int len)
{
	// 步长
	int gap = len;

	
	int i = -1;
	int j = -1;
	int k = -1;

	while (gap > 1)
	{
		// 步长递减公式
		gap = gap / 3 + 1;

		// 分组, 对每一组, 进行插入排序
		for (i = 0; i < gap; ++i)
		{
			int tmp;	// 基准数
			int index;	// 坑的位置

			// 插入排序
			// 无序序列
			for (j = i + gap; j < len; j += gap)
			{
				tmp = array[j];
				index = j;

				// 有序序列(从后往前遍历)
				for (k = j - gap; k >= 0; k -= gap)
				{
					if (tmp < array[k])
					{
						// 后移
						array[k + gap] = array[k];
						// 位置
						index = k;
					}
					else
					{
						break;
					}
				}
				// 填坑
				array[index] = tmp;
			}
		}
	}
}

#if 1
void main()
{
	int i = -1;

	//定义整型数组
	int array[] = { 12, 5, 33, 6, 10 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	//排序
	shellSort(array, len);

	//遍历
	printf("希尔排序之后的序列:	");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

运行结果：

5.5 关于希尔排序步长的说明

• 步长的计算公式可以自行制定，最后步长 == 1 即可。

• 通过大量测试得出的结论：步长 = 步长 / 3 + 1

5.6 稳定性

• 希尔排序是不稳定的排序算法

• 希尔排序的效率：(O（n*logn）) ≈ (O（1.3*n）)

6 快速排序

6.1 算法介绍

快速排序是C.R.A.Hoare于1962年提出的一种 划分交换排序。它 采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

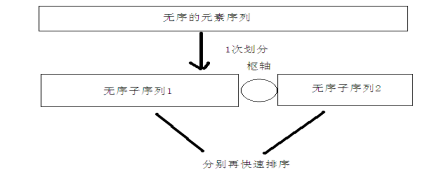
6.2 基本思想

1. 先从元素序列中取出一个数作为基准数（枢轴）

2. 分区过程：将比这个数大的数全放在它的右边，小于或等于它的数全放在它的左边。（升序）

3. 再对左右区间重复第 2 步，直到各个区间只有一个数

6.3 算法实现

#include <stdio.h>
#include <stdlib.h>

//快速排序
void quickSort(int s[], int l, int r)
{
	if (l < r)
	{
		int i = l, j = r;
		// 拿出第一个元素, 保存到x中,第一个位置成为一个坑
		int x = s[l];

		while (i < j)
		{
			// 从右向左找小于x的数
			while (i < j && s[j] >= x)
			{
				//左移, 直到遇到小于等于x的数
				j--;
			}

			if (i < j)
			{
				//将右侧找到的小于x的元素放入左侧坑中, 右侧出现一个坑
				//左侧元素索引后移
				s[i++] = s[j];
			}

			// 从左向右找大于等于x的数
			while (i < j && s[i] < x)
			{
				//右移, 直到遇到大于x的数
				i++;
			}

			if (i < j)
			{
				//将左侧找到的元素放入右侧坑中, 左侧出现一个坑
				//右侧元素索引向前移动
				s[j--] = s[i];
			}
		}

		//此时 i=j,将保存在x中的数填入坑中
		s[i] = x;

		quickSort(s, l, i - 1); // 递归调用 

		quickSort(s, i + 1, r);
	}
}

#if 1
void main()
{
	int i = -1;

	//定义整型数组
	int array[] = { 12, 5, 33, 6, 10 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	//排序
	quickSort(array, 0, len-1);

	//遍历
	printf("快速排序之后的序列:	");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

运行结果：

6.4 稳定性

• 快速排序是一种不稳定的排序算法

• 排序效率： (O（n*logn）)

7 归并排序

7.1 算法介绍

归并排序是 建立在归并操作上的一种有效的排序算法。该算法是 采用分治法（Divide and Conquer）的一个非常典型的应用。

7.2 基本思想

基本思路就是将数组分成二组A，B，如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。

如何让这二组组内数据有序了？

可以将A，B 组各自再分成二组。依次类推，当分出来的小组只有一个数据时，可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先递归的分解数列，再合并数列就完成了归并排序。

7.3 归并的定义

将两个或两个以上的 有序序列合并成一个新的有序序列：有序序列 V[1] ~ V[m] 和 V[m+1]~ V[n] ---> V[1] ~ V[n]，这种归并方法称为 2 路归并

7.4 如何合并两个有序序列

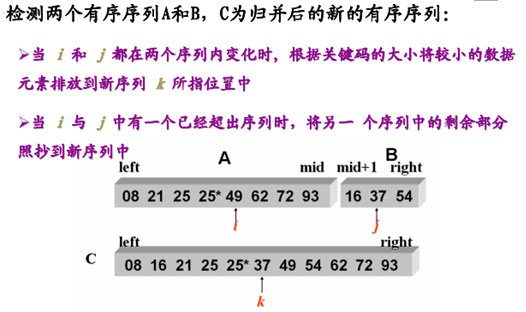
7.4.1 代码实现

// 将两个有序数列a[first...mid]和a[mid+1...last]合并。
void mergeArray(int a[], int first, int mid, int last, int temp[])
{
	int leftStart = first;	//左有序序列起点
	int leftEnd = mid;	//左有序序列终点
	int rightStart = mid + 1;	//右有序序列起点
	int rightEnd = last;	//右有序序列终点
	int length = 0;	//两个有序序列合并之后的有序序列长度
	int i = leftStart, j = rightStart;
	
	// 将两个有序序列中的元素合并到第三个有序序列中(a的左半部分和右半部分合并到temp中)
	while (i <= leftEnd && j <= rightEnd)
	{
		// 按照从小到大的顺序放入到temp中
		if (a[i] <= a[j])
		{
			temp[length++] = a[i++];
		}
		else
		{
			temp[length++] = a[j++];
		}
	}

	// 如果左半部分还有元素, 直接放到temp中
	while (i <= leftEnd)
	{
		temp[length++] = a[i++];
	}

	// 如果右半部分还有元素, 直接放到temp中
	while (j <= rightEnd)
	{
		temp[length++] = a[j++];
	}

	// 将temp中排好的序列拷贝到a数组中
	for (i = 0; i < length; i++)
	{
		// 只替换已排好序的那一部分
		a[leftStart + i] = temp[i];
	}
}

7.5 排序过程

7.6 算法实现

#include <stdio.h>
#include <stdlib.h>

// 将两个有序数列a[first...mid]和a[mid+1...last]合并。
void mergeArray(int a[], int first, int mid, int last, int temp[])
{
	int leftStart = first;	//左有序序列起点
	int leftEnd = mid;	//左有序序列终点
	int rightStart = mid + 1;	//右有序序列起点
	int rightEnd = last;	//右有序序列终点
	int length = 0;	//两个有序序列合并之后的有序序列长度
	int i = leftStart, j = rightStart;
	
	// 将两个有序序列中的元素合并到第三个有序序列中(a的左半部分和右半部分合并到temp中)
	while (i <= leftEnd && j <= rightEnd)
	{
		// 按照从小到大的顺序放入到temp中
		if (a[i] <= a[j])
		{
			temp[length++] = a[i++];
		}
		else
		{
			temp[length++] = a[j++];
		}
	}

	// 如果左半部分还有元素, 直接放到temp中
	while (i <= leftEnd)
	{
		temp[length++] = a[i++];
	}

	// 如果右半部分还有元素, 直接放到temp中
	while (j <= rightEnd)
	{
		temp[length++] = a[j++];
	}

	// 将temp中排好的序列拷贝到a数组中
	for (i = 0; i < length; i++)
	{
		// 只替换已排好序的那一部分
		a[leftStart + i] = temp[i];
	}
}

// 归并排序
void mergeSort(int a[], int first, int last, int temp[])
{
	if (first < last)
	{
		// 找到数组的中间位置
		int mid = (first + last) / 2;
		// 左边有序
		mergeSort(a, first, mid, temp);  
		// 右边有序
		mergeSort(a, mid + 1, last, temp); 
		// 再将二个有序数列合并
		mergeArray(a, first, mid, last, temp); 
	}
}

#if 1
void main()
{
	int i = -1;

	//定义整型数组
	int array[] = { 12, 5, 33, 6, 10 };
	//计算数组长度
	int len = sizeof(array) / sizeof(int);

	//创建合适大小的临时数组
	int *p = (int*)malloc(sizeof(int) * len);

	if (p == NULL)
	{
		return;
	}

	//遍历数组
	printf("待排序数组序列: ");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	mergeSort(array, 0, len - 1, p);

	free(p);

	//遍历
	printf("归并排序之后的序列:	");

	for (i = 0; i < len; ++i)
	{
		printf("%d	", array[i]);
	}

	printf("
");

	system("pause");
}
#endif

运行结果：

7.7 稳定性

• 归并排序是一种稳定的排序算法。

• 排序效率： (O（n*logn）)

8 总结

排序算法	平均时间复杂度	最坏时间复杂度	平均空间复杂度	稳定性
选择排序	(O({n^2}))	(O({n^2}))	(O(1))	不稳定
冒泡排序	(O({n^2}))	(O({n^2}))	(O(1))	稳定
直接插入排序	(O({n^2}))	(O({n^2}))	(O(1))	稳定
希尔排序	(O({nlogn}))	(O({n^2}))	(O({nlog_2n}))	不稳定
快速排序	(O({nlogn}))	(O({n^2}))	(O(1))	不稳定
归并排序	(O({nlogn}))	(O({nlogn}))	(O(n))	稳定