剑指 Offer II 007. 数组中和为 0 的三个数
题目描述
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a ,b ,c ,使得 a + b + c = 0 ?请找出所有和为 0 且 不重复 的三元组。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/1fGaJU
关键是怎么做到不重复
题解
这道题是的升级版,其实只要外面套一层for循环就好了。问题是怎么去重,可以用集合(额外增加复杂度)。主要是算法优化
返回的是三元组[i,j,k]
首先排序一下,使第一个元素不充分 nums[i] == nums[i-1]跳过即可
使第二个元素不重复计算 nums[j] == nums[j-1]跳过即可
第三个要不要考虑,当然要,但是如果排序了的话,就解决了
def threeSum(self, nums: List[int]) -> List[List[int]]: #找出所有 #和为 0 且 不重复 的三元组 # 首先排序 nums.sort() length = len(nums) ret = [] for i in range(length-2): if nums[i]>0:break # 对第一个元素去重复 if i>0 and nums[i]==nums[i-1]:continue j = i+1 k = length-1 while j<k: sum = nums[i]+nums[j]+nums[k] if sum ==0: ret.append([nums[i],nums[j],nums[k]]) #对第二个元素去重 second = nums[j] while j<k and nums[j] == second: j+=1 elif sum<0: j+=1 else: k-=1 return ret
剑指 Offer II 008. 和大于等于 target 的最短子数组
题目描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/2VG8Kg
题解
滑动窗口
连续子数组优先想到滑动窗口
def minSubArrayLen(self, target: int, nums: List[int]) -> int: # 优化首轮有没有最优解1 if nums.count(target)>0:return 1 # 滑动窗口 start,end = 0,0 n = len(nums) minimun = n+1 sums = 0 while end<n: sums+=nums[end] # 如果窗口和大于等于target,更新最小值,并缩小窗口 while sums >= target: minimun = min(minimun,end-start+1) sums -=nums[start] start+=1 # 扩大窗口 end+=1 return 0 if minimun == n+1 else minimun
前缀和方法
由于数列中的元素都是正整数,所以前缀和函数是单调递增的
def minSubArrayLen(self, target: int, nums: List[int]) -> int: # 优化首轮有没有最优解1 if nums.count(target)>0:return 1 # 前缀和 单调函数 可以拓展到二分 left,temp = 0,0 n = len(nums) res = n+1 for right in range(n): temp += nums[right] #前缀和 while left <= right and temp >= target: res = min(res,right - left + 1) temp -= nums[left] left += 1 return res if res != n+1 else 0
可以用二分法优化里面的查找
剑指 Offer II 009. 乘积小于 K 的子数组
题目描述
给定一个正整数数组 nums和整数 k ,请找出该数组内乘积小于 k 的连续的子数组的个数。
剑指 Offer II 009. 乘积小于 K 的子数组 - 力扣(LeetCode) (leetcode-cn.com)
题解
滑动窗口
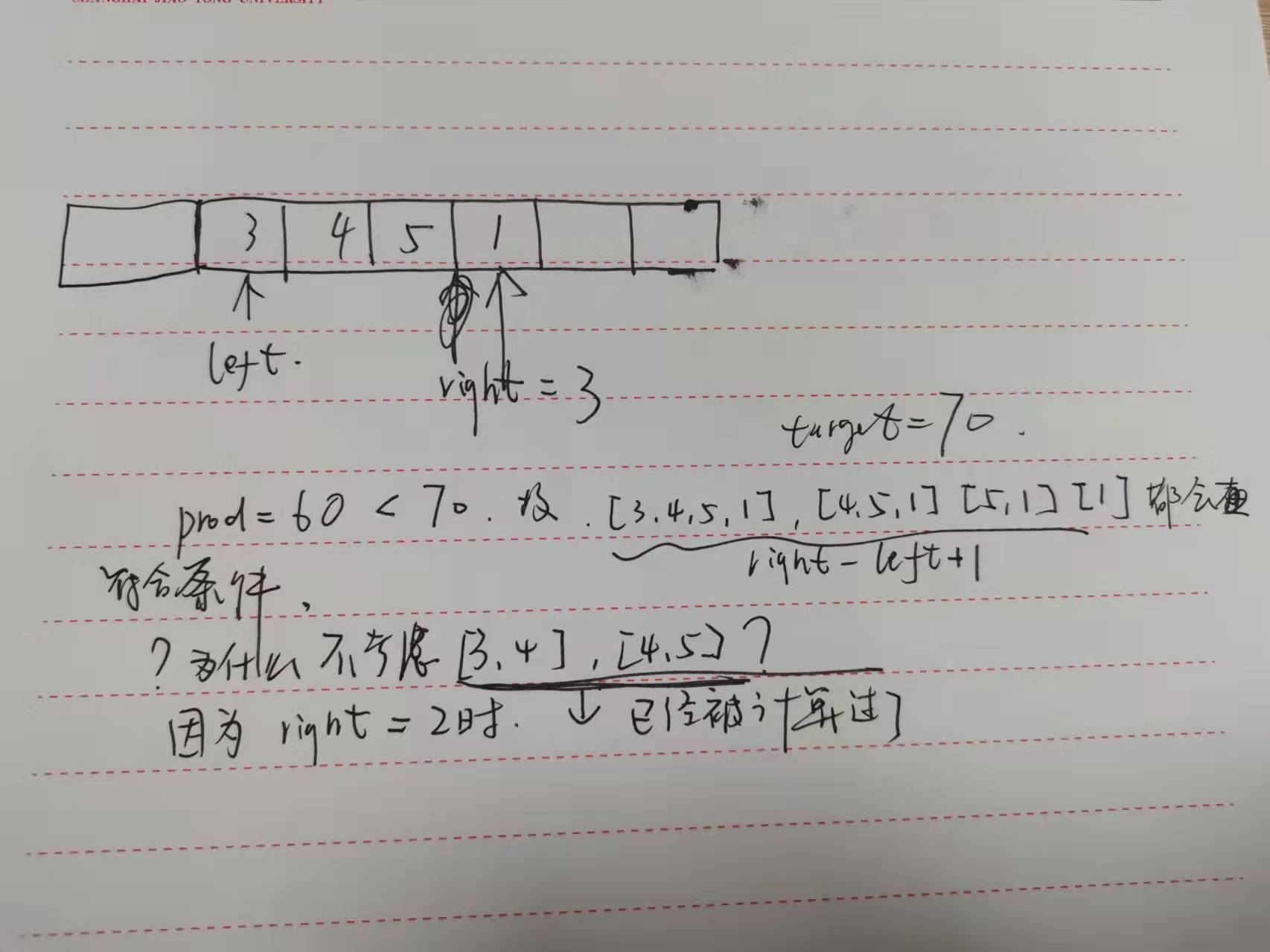
def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int: # 正整数数组 连续的子数组 找...的个数 # 滑动窗口1 left,ret= 0,0 n = len(nums) prod=1 for right,num in enumerate(nums): prod*=num while left<=right and prod>=k: prod //= nums[left] left+=1 # 找到了左边界,由于都是正整数的原因,左边界再往左都会成立,只要左边界在右边界的左或等 if left <=right: ret += right-left+1 return ret
- 为什么enumerate数组的右边界?保证不会越界
剑指 Offer II 010. 和为 k 的子数组
题目描述
给定一个整数数组和一个整数 k ,请找到该数组中和为 k 的连续子数组的个数。
剑指 Offer II 010. 和为 k 的子数组 - 力扣(LeetCode) (leetcode-cn.com)
题解
整数数组有负数不太能用二分法,考虑前缀和方法
前缀和
- 遍历数组一次
- 字典的键key是前缀和,字典的值是前面有几个前缀和为key的位置
def subarraySum(self, nums: List[int], k: int) -> int: # 整数数组 连续子数组 # 可能有负数,滑动窗口不好用了 left,ret = 0,0 sums = 0 # 字典的键key是前缀和,字典的值是前面有几个前缀和为key的位置 sums_dict = {0:1} for num in nums: sums +=num #前缀和 ret += sums_dict.get(sums-k,0) sums_dict[sums] = sums_dict.get(sums,0)+1 return ret
剑指 Offer II 011. 0 和 1 个数相同的子数组
题目描述
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
剑指 Offer II 011. 0 和 1 个数相同的子数组 - 力扣(LeetCode) (leetcode-cn.com)
题解
小技巧,把0变-1的话,就有不变的target了,即0,就可以使用前缀和来做,不然的话不好给条件
前缀和
- 题目求最长的连续子数组,故hash表只要记录第一次遇到的前缀和
- 如果遍历前缀和list过程中,发现字典中有当前前缀和,就说明添加的这些元素的和刚好等于target(把0变成-1,那么这里的target就是0 )
def findMaxLength(self, nums: List[int]) -> int: n = len(nums) #将所有0转化为-1,那么如果遇到了相同数量的0和1,累加之后的结果就为0,转化为前缀和,k=0 pre_dict = {0:-1} ret,pre_sum = 0,0 for index,num in enumerate(nums): pre_sum += 1 if num ==1 else -1 # 如果加了个寂寞 if pre_sum in pre_dict: ret = max(ret, index-pre_dict[pre_sum]) else: # 如果初次见面 pre_dict[pre_sum] = index return ret
剑指 Offer II 012. 左右两边子数组的和相等
题目描述
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/tvdfij
题解

前缀和
- 由于最左边也可以视为中心下标且左端值视为0,那么前缀和最开始的时候便插入一个0
- 如果最右端可以是中心下标,那么最左端也是中心下标,返回最左端
def pivotIndex(self, nums: List[int]) -> int: pre_sum = [0] tmp = 0 for num in nums: tmp+=num pre_sum.append(tmp) # 剩下的问题就只和前缀和数组有关了 for index,pre in enumerate(pre_sum[:-1]): if pre == pre_sum[-1] - pre_sum[index+1]: return index return -1 ''' # 这个方法为什么不行,因为没有考虑边界 pre_sum = [] tmp = 0 for num in nums: tmp+=num pre_sum.append(tmp) for index,pre in enumerate(pre_sum[:-1]): if pre_sum[index-1] == pre_sum[-1] - pre: return index return -1 '''
剑指 Offer II 013. 二维子矩阵的和
题目描述
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
实现 NumMatrix 类:
- NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
- int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/O4NDxx题解
还是用前缀和的方法就可以做,有点像动态规划
- i,j位置记录了i,j 到左下角所有位置的前缀和
- 注意最下面一行和最左边一列的初始化
- 注意返回时的数组越界问题
| 0,0 | 0,4 | |||
| 1,0 | ||||
| i,j | ||||
| 4,0 | 4,4 |
前缀和
def __init__(self, matrix: List[List[int]]): rows,columns = len(matrix),len(matrix[0]) # 初始化 self.presum_table = [[0 for c in range(columns)] for r in range(rows)] # 求前缀和,从左开始一层一层往上往右求 # 最左边和最下面一行就等于matrix的值 for j in range(columns): self.presum_table[rows-1][j] = matrix[rows-1][j] + self.presum_table[rows-1][j-1] for i in list(range(rows))[:-1][::-1]: self.presum_table[i][0] = matrix[i][0] +self.presum_table[i+1][0] # 从(1,1)开始往上求和 for i in list(range(rows))[::-1][1:]: for j in list(range(columns))[1:]: self.presum_table[i][j] = self.presum_table[i][j-1] + self.presum_table[i+1][j] - self.presum_table[i+1][j-1] + matrix[i][j] def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int: rows,columns = len(self.presum_table),len(self.presum_table[0]) if row2==rows-1 and col1 == 0: return self.presum_table[row1][col2] if row2==rows-1: return self.presum_table[row1][col2]-self.presum_table[row1][col1-1] if col1 == 0: return self.presum_table[row1][col2]-self.presum_table[row2+1][col2] if row2<rows-1 and col1>=1: ret = self.presum_table[row1][col2]-self.presum_table[row1][col1-1]-self.presum_table[row2+1][col2]+self.presum_table[row2+1][col1-1] return ret
现在问题来了,为什么大佬的代码那么短啊!!!!?
def __init__(self, matrix: List[List[int]]): m, n = len(matrix), (len(matrix[0]) if matrix else 0) self.sums = [[0] * (n + 1) for _ in range(m + 1)] _sums = self.sums for i in range(m): for j in range(n): _sums[i + 1][j + 1] = _sums[i][j + 1] + _sums[i + 1][j] - _sums[i][j] + matrix[i][j] def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int: _sums = self.sums return _sums[row2 + 1][col2 + 1] - _sums[row1][col2 + 1] - _sums[row2 + 1][col1] + _sums[row1][col1]
[0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 0, 0, 0, 0, 0] [0, 3, 3, 4, 8, 10] [0, 8, 14, 18, 24, 27] [0, 9, 17, 21, 28, 36] [0, 13, 22, 26, 34, 49] [0, 14, 23, 30, 38, 58]
可以看到大佬的前缀和矩阵是6*6的,但是数据只有5*5
主要是边界不好取,只要多一个格子存边界前,或者边界下,anyway, 全0 ,那么最后就可以省很多代码,上上面的方法用于原地修改比较好
- 前缀和改进
row不变,因为全0加在底下,但是col却要变,因为加了一列全0在左边,固col标号+1
def __init__(self, matrix: List[List[int]]): rows,columns = len(matrix),len(matrix[0]) # 初始化 self.presum_table = [[0 for c in range(columns+1)] for r in range(rows+1)] # 求前缀和,从左开始一层一层往上往右求 # 最左边和最下面一行就等于matrix的值 for i in list(range(rows+1))[::-1][1:]: for j in list(range(columns+1))[1:]: self.presum_table[i][j] = self.presum_table[i][j-1] + self.presum_table[i+1][j] - self.presum_table[i+1][j-1] + matrix[i][j-1] def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int: ret = self.presum_table[row1][col2+1]-self.presum_table[row1][col1-1+1]-self.presum_table[row2+1][col2+1]+self.presum_table[row2+1][col1-1+1] return ret
欸现在我的代码也很短了