add(a,b)
不用+-*/运算符 实现add(a,b)
题目来源:https://leetcode-cn.com/problems/bu-yong-jia-jian-cheng-chu-zuo-jia-fa-lcof
C++:
int add(int a, int b) { //循环终止条件 没有进位了为止 while (b != 0) { //保存进位和 int c = (unsigned int)(a & b) << 1; //c++中,负数不支持左移,把符号位给移了怎么办? //保存无进位和 a = a ^ b; //如果还有进位 c!=0,再循环,如果没有,输出无进位和a b = c; } return a; }
Python:
def add(self, a: int, b: int) -> int: """ # 写法1 递归 if b==0: return a return add(a^b,(a&b)<<1); """ # 2 循环 x = 0xffffffff a,b = a&x,b&x while b!=0: a,b = a^b, (a&b)<<1 &x return a if a<=0x7fffffff else ~(a^x)
- 为什么a,b = a&x,b&x?
取补码 - 为什么a<=0x7ffffffff返回~(a^x)?
负数的补码a-> 还原为->负数本身~(a^x)
负数在python中的存储问题(python可能会将负数的补码看成正数,所以用到时候需要还原负数)
- 正数的补码即本身
- 负数的补码在反码的基础上+1
Python,Java 等语言中的数字都是以 补码 形式存储的。 Python 没有 int , long 等不同长度变量,即在编程时无变量位数的概念。
- 获取负数的补码: 需要将数字与十六进制数 0xffffffff 相与。可理解为舍去此数字 32 位以上的数字(将 32 位以上都变为 00 ),从无限长度变为一个 32 位整数。
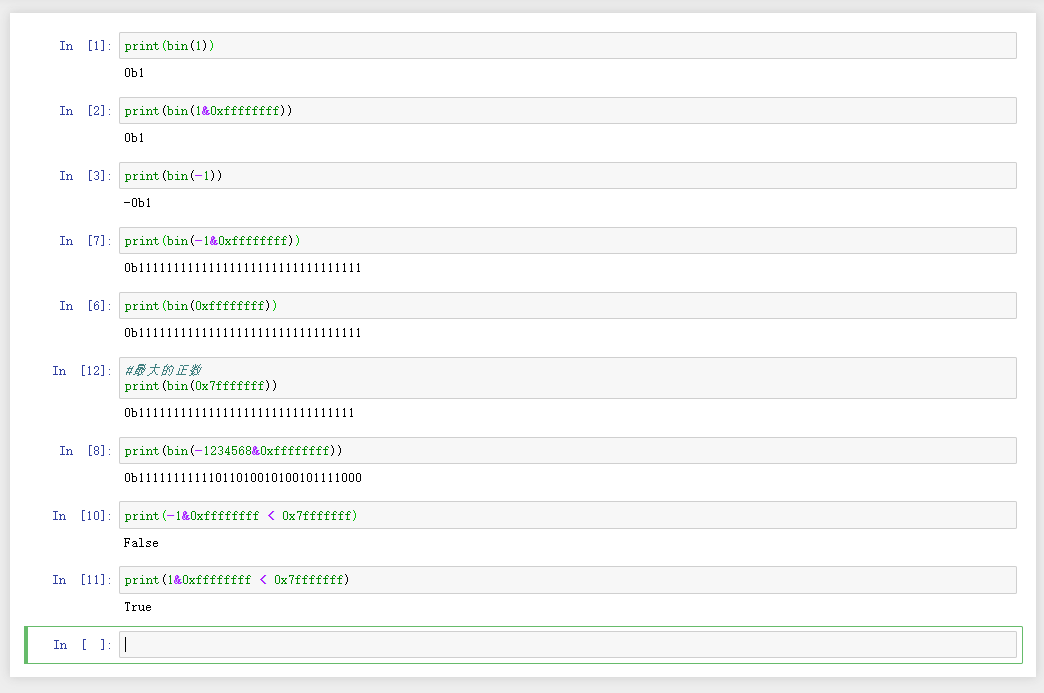
- 返回前数字还原: 若补码 a 为负数( 0x7fffffff 是最大的正数的补码 2147483647 即 01111111111111111111111111111111),需执行 ~(a ^ x) 操作,将补码还原至 Python 的存储格式。
a ^ x 运算将 1 至 32 位按位取反; ~ 运算是将整个数字取反;因此, ~(a ^ x) 是将 32 位以上的位取反,1 至 32 位不变。
例子:python的负数补码情况_hxshine的博客-CSDN博客_python 负数补码
vector<int> singleNumbers(vector<int>& nums)
输入数组是【a,a,b,b,c,x,c,d,d,e,e,f,x,f,g,g,....】中有两个数是single其它是两个,要求O(N) O(1)算法输出数组中只出现一次的那两个数
源自leetcode题目:https://leetcode-cn.com/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/
python:
def singleNumbers(self, nums: List[int]) -> List[int]: x,y,xorSum,suppBitOfxOry = 0,0,0,1 # 计算x xor y for num in nums: xorSum ^=num # 找到任意一个supp(x xor y) while not xorSum & suppBitOfxOry: suppBitOfxOry = suppBitOfxOry << 1 # 用一个bit位将nums分成两个集合 【x,a,a,b,b,c,c,d,d,...】 【y,e,e,f,f,g,g,h,h,...】 两个相同的数一定在同一个集合中 # 这两个只出现一次的数字x,y与m做"与运算"时,一个结果会是0,一个非0 根据这个性质做区分 # 至于其他的数同样可以被这个bit分为两部分,而且任意一对相同的两个数被分到了一起 不管它匹配了x还是y都无所谓,因为最后会被异或给消去 for num in nums: if num & suppBitOfxOry: # 【x,a,a,b,b,c,c,d,d,...】 根据异或性质只会留下x x^=num else: y^=num return x,y
c++:
vector<int> singleNumbers(vector<int>& nums) { int xorSum = 0; int x=0,y=0; int oneSuppBitOfxOry = 1; for(int i=0;i<nums.size();i++){ xorSum ^=nums[i]; } while((xorSum & oneSuppBitOfxOry)==0) oneSuppBitOfxOry=oneSuppBitOfxOry<<1;//注意这里的运算符优先级 写成while(xorSum & oneSuppBitOfxOry==0) 出大问题 for(int i=0;i<nums.size();i++){ if((nums[i]&oneSuppBitOfxOry)==0){ x^=nums[i]; }else{ y^=nums[i]; } } vector<int> res; res.push_back(x); res.push_back(y); return res; }
P.S. 运算符优先级(copy 百度百科)
|
优先级
|
运算符
|
名称或含义
|
使用形式
|
结合方向
|
说明
|
|
1
|
[]
|
数组下标
|
数组名[常量表达式]
|
左到右
|
|
|
()
|
圆括号
|
(表达式)/函数名(形参表)
|
|||
|
.
|
成员选择(对象)
|
对象.成员名
|
|||
|
->
|
成员选择(指针)
|
对象指针->成员名
|
|||
|
2
|
-
|
负号运算符
|
-表达式
|
右到左
|
单目运算符
|
|
(类型)
|
强制类型转换
|
(数据类型)表达式
|
|||
|
++
|
前置自增运算符
|
++变量名
|
单目运算符
|
||
|
++
|
后置自增运算符
|
变量名++
|
单目运算符
|
||
|
--
|
前置自减运算符
|
--变量名
|
单目运算符
|
||
|
--
|
后置自减运算符
|
变量名--
|
|||
|
*
|
取值运算符
|
*指针变量
|
单目运算符
|
||
|
&
|
取地址运算符
|
&变量名
|
单目运算符
|
||
|
!
|
逻辑非运算符
|
!表达式
|
单目运算符
|
||
|
~
|
按位取反运算符
|
~表达式
|
单目运算符
|
||
|
sizeof
|
长度运算符
|
sizeof(表达式)
|
|||
|
3
|
/
|
除
|
表达式/表达式
|
左到右
|
双目运算符
|
|
*
|
乘
|
表达式*表达式
|
双目运算符
|
||
|
%
|
余数(取模)
|
整型表达式/整型表达式
|
双目运算符
|
||
|
4
|
+
|
加
|
表达式+表达式
|
左到右
|
双目运算符
|
|
-
|
减
|
表达式-表达式
|
双目运算符
|
||
|
5
|
左移
|
变量
|
左到右
|
双目运算符
|
|
|
>>
|
右移
|
变量>>表达式
|
双目运算符
|
||
|
6
|
>
|
大于
|
表达式>表达式
|
左到右
|
双目运算符
|
|
>=
|
大于等于
|
表达式>=表达式
|
双目运算符
|
||
|
小于
|
表达式
|
双目运算符
|
|||
|
小于等于
|
表达式
|
双目运算符
|
|||
|
7
|
==
|
等于
|
表达式==表达式
|
左到右
|
双目运算符
|
|
!=
|
不等于
|
表达式!= 表达式
|
双目运算符
|
||
|
8
|
&
|
按位与
|
表达式&表达式
|
左到右
|
双目运算符
|
|
9
|
^
|
按位异或
|
表达式^表达式
|
左到右
|
双目运算符
|
|
10
|
|
|
按位或
|
表达式|表达式
|
左到右
|
双目运算符
|
|
11
|
&&
|
逻辑与
|
表达式&&表达式
|
左到右
|
双目运算符
|
|
12
|
||
|
逻辑或
|
表达式||表达式
|
左到右
|
双目运算符
|
|
13
|
?:
|
条件运算符
|
表达式1? 表达式2: 表达式3
|
右到左
|
三目运算符
|
|
14
|
=
|
赋值运算符
|
变量=表达式
|
右到左
|
|
|
/=
|
除后赋值
|
变量/=表达式
|
|||
|
*=
|
乘后赋值
|
变量*=表达式
|
|||
|
%=
|
取模后赋值
|
变量%=表达式
|
|||
|
+=
|
加后赋值
|
变量+=表达式
|
|||
|
-=
|
减后赋值
|
变量-=表达式
|
|||
|
左移后赋值
|
变量
|
||||
|
>>=
|
右移后赋值
|
变量>>=表达式
|
|||
|
&=
|
按位与后赋值
|
变量&=表达式
|
|||
|
^=
|
按位异或后赋值
|
变量^=表达式
|
|||
|
|=
|
按位或后赋值
|
变量|=表达式
|
|||
|
15
|
,
|
逗号运算符
|
表达式,表达式,…
|
左到右
|
从左向右顺序运算
|
说明:
同一优先级的运算符,运算次序由结合方向所决定。
简单记就是:! > 算术运算符 > 关系运算符 > && > || > 赋值运算符
int singleNumber(vector<int>& nums)
输入数组是【aaabbbcccdddexeefffgggiii,....】中有1个数是single其它是triple,输出数组中只出现一次的那个数
题目来源leetcode,K神题解:面试题56 - II. 数组中数字出现的次数 II(位运算 + 有限状态自动机,清晰图解) - 数组中数字出现的次数 II - 力扣(LeetCode) (leetcode-cn.com)
python:
def singleNumber(self, nums: List[int]) -> int: # hash表 谁都会写 面试有啥用? 面试一写就offer挂啦 # 位运算 + 有限状态自动机 什么脑洞 AAAAAAAAAAAAAAAAAAWWWWWWWWWWWWWWWWWWWWWWW # 对于最低位而言 这个位上有多少个1记为wt(b_0) wt(b_0) mod 3 in {0,1,2} 三种状态 00 01 10 分别对应表示0,1,2 # 直接应用在所有的位上逻辑同样成立 a,b = 0,0 for num in nums: a = ~b &(num^a) # 状态高位是在状态地位修改后的基础上修改的 b = ~a &(num^b) # 因为状态的缘故 只关心状态啊=的地位就可以 就是说当所有的数加上之后,状态的高位肯定是0 return a
更应该关注的是状态如何转移 和 如何简化代码!
本题的技巧:观察真值表 和 利用位运算符来替代条件判断语句
