基本数论

素数是数论的核心

整数p>1是素数，当且仅当它的因子只有±1和±p.

介绍算术基本定理：

简单copy一下：https://wenku.baidu.com/view/d0a116035acfa1c7ab00cc69.html

数论基本定理

定理1：

 

证明：

定理2：

证明：

推论：

证明：

定理3：

 

证明：

定理4：（算术基本定理）

 这种表达是唯一的

证明：

 

推论1：

 证明：

推论2：

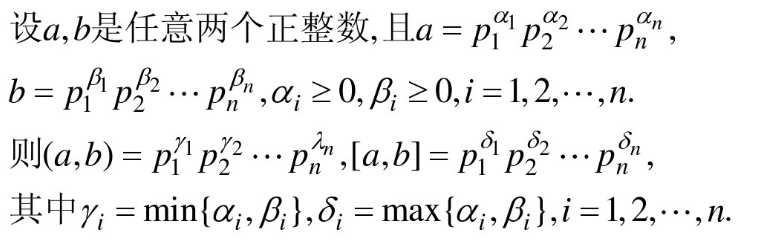
费马定理+欧拉定理

费马定理：

　　若p是素数，a是正整数且不能被p整除，则：

　　a^p-1 ≡ 1 (mod p)

欧拉函数Φ(n)：

　　Φ(n)是小于n且与n互素的正整数的个数。

函欧拉定理：

 　　对于任何互素的a和n，有

　　a^Φ(n)  ≡ 1 (mod n)

素性测试

许多密码算法都需要随机选择一个或者多个非常非常大的素数。

我们需要有一种方法测定一个确定的数是否是素数。===> 素性测试   下面给出两个方法  简单的测试和Rabin-Miller算法：

简单的测试算法：

# Prime Number Sieve
# http://inventwithpython.com/hacking (BSD Licensed)

import math


def isPrime(num):
    # Returns True if num is a prime number, otherwise False.

    # Note: Generally, isPrime() is slower than primeSieve().

    # all numbers less than 2 are not prime
    if num < 2:
        return False

    # see if num is divisible by any number up to the square root of num
    for i in range(2, int(math.sqrt(num)) + 1):
        if num % i == 0:
            return False
    return True


def primeSieve(sieveSize):
    # Returns a list of prime numbers calculated using
    # the Sieve of Eratosthenes algorithm.

    sieve = [True] * sieveSize
    sieve[0] = False # zero and one are not prime numbers
    sieve[1] = False

    # create the sieve
    for i in range(2, int(math.sqrt(sieveSize)) + 1):
        pointer = i * 2
        while pointer < sieveSize:
            sieve[pointer] = False
            pointer += i

    # compile the list of primes
    primes = []
    for i in range(sieveSize):
        if sieve[i] == True:
            primes.append(i)

    return primes

isPrime(num)

　　检查给定的数是否能整除2~sqrt(num)之间的整数。而不必检查2~num之间的所有整数。

 

primeSieve(sieveSize)

　　利用埃拉托色尼（Eratosthenes）筛选法  

 

　　1.比如找50以内的的所有质数建立一个这样的表，把每个数标记为质数：

　　2.把1标记为非质数

　　3.把所有2的倍数（除了2本身）标记为非质数

　　4.把所有3的倍数（除了3本身）标记为非质数

　　5.把所有4的倍数（除了4本身）标记为非质数

　　重复该过程

　　直到8为止（为什么是8？    答：int(math.sqrt(50) = 8）

 做完了这些，我们可以看到，表格中留白的都是质数。

但是这个简单的算法是有局限性的，对于大的数时，就略显乏力了

 著名的 Rabin-Miller算法：

背景：

n≥3的整奇数n可以表示为：

　　n-1 = 2^kq       其中：k>0, q是奇数，n-1是个偶数！

素数第一性质：

　　若p是素数，a是小于p的正整数，则 a² mod p = 1, 当且仅当

　　　　a mod p = 1 或者 a mod p = -1 mod p = p -1

素数第二性质：

　　设p是大于2的素数（p.s. 肯定是个奇数，满足p-1 = 2^kq, 其中：k>0, q是奇数); 设a是整数且1<a<p-1，则必有下面两个条件之一成立：

• a^q 模 p 和 1 同余， 即 a^q mod p = 1 或者说：  a^q ≡ 1（mod p）
• 整数 a^q, a^2q, a^4q, ... , a^{2^(k-1)·q}中存在一个数， 模p时和-1同余。

详细的算法

1. 找出整数k, q, 其中 k>0, q是奇数， 使（n-1 = 2^kq ）；
2. 随机选取整数a， 1<a<n-1；
3. if a^q mod n = 1, then 返回     不确定；
4. for j=0 to k-1 do:
5. 　　if a^2jq mod n = n-1 ,then 返回   不确定
6. 返回"合数"

重复使用Rabin-Miller算法：提高“不确定”的可信度

选择多个（t）不同的整数a，他们都能通过测试（返回不确定）的概率小于(1/4)^t     p.s. 某篇论文证明的哈哈哈哈哈哈

因此，取足够大的t，如果Miller测试总是返回“不确定”， 我们能以很大的把握说n是素数。

# Primality Testing with the Rabin-Miller Algorithm
# http://inventwithpython.com/hacking (BSD Licensed)

import random

# 测试是不是质数的算法主体  .
def rabinMiller(num):
    # Returns True if num is a prime number.


    # 找出整数t, s, 其中 t>0, q是奇数， 使 n-1 = (2^t)*s ；
    s = num - 1
    t = 0
    while s % 2 == 0:
        # keep halving s until it is even (and use t
        # to count how many times we halve s)
        s = s // 2
        t += 1

    # 随机选取整数a， 1<a<n-1；选择不同的a的次数越多，就越准确地‘判断’
    for trials in range(5): # try to falsify num's primality 5 times
        # random.randrange的函数原型为：random.randrange([start], stop[, step])，从指定范围内，按指定基数递增的集合中 获取一个随机数。
        a = random.randrange(2, num - 1)
        # 函数是计算 x 的 y 次方，如果 z 在存在，则再对结果进行取模，其结果等效于 pow(x,y) %z
        v = pow(a, s, num)
        # if a^s mod num = 1, then if不进入返回  一次   不确定；
        if v != 1: # this test does not apply if v is 1.
            i = 0
            
            while v != (num - 1):
                if i == t - 1:
                    return False
                else:
                    i = i + 1
                    v = (v ** 2) % num
    return True


def isPrime(num):
    # Return True if num is a prime number. This function does a quicker
    # prime number check before calling rabinMiller().

    if (num < 2):
        return False # 0, 1, and negative numbers are not prime

    # About 1/3 of the time we can quickly determine if num is not prime
    # by dividing by the first few dozen prime numbers. This is quicker
    # than rabinMiller(), but unlike rabinMiller() is not guaranteed to
    # prove that a number is prime.
    lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]

    if num in lowPrimes:
        return True

    # See if any of the low prime numbers can divide num
    for prime in lowPrimes:
        if (num % prime == 0):
            return False

    # If all else fails, call rabinMiller() to determine if num is a prime.
    return rabinMiller(num)


def generateLargePrime(keysize=1024):
    # Return a random prime number of keysize bits in size.
    while True:
        num = random.randrange(2**(keysize-1), 2**(keysize))
        if isPrime(num):
            return num