模运算基本概念
对于一个钟表来说,我们知道他从0点开始到12点结束(可以这么理解),很容易知道
5点+3点 = 8点
那么,9点+ 200点 的时候,时针再哪呢? 答 :
209 -12 = 197
197 - 12 = 185
....
17 -12 = 5
这种“回调”叫做取模运算(modular arithmetic) 我们说 17 模 12 等于 5
Python中模运算符是 %
某种程度上,我们可以说:“模” 是 “余数”
还需要记住,计算机中模运算的结果都是正数, 有方便的计算手段 :
209 % 12 = 5 即数学上 209 mod 12 = 5
>>> 209 mod 12 File "<stdin>", line 1 209 mod 12 ^ SyntaxError: invalid syntax >>> 209 % 12 5 >>> -21 % 12 3 >>> -21 % 5 4 >>>
P.S. 多重赋值
>>> a, b = 45, 687 >>> a, b (45, 687) >>> a 45 >>> c, v, n, m = ['sad', 456, 'a', a] >>> v 456 >>> v 456 >>> n 'a' >>> c 'sad' >>> m 45 >>> q, w, e = [555, 888] Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: not enough values to unpack (expected 3, got 2) >>> q, w, e = [555, 888, 999, 'dasdsd'] Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: too many values to unpack (expected 3) >>>
要求 : 赋值运算符''="左右两边的项要相等
可以使用多重赋值来方便地交换值
>>> a, b = 45, 79 >>> a, b = b, a >>> a, b (79, 45) >>>
欧几里得算法---找两个正整数的GCD
GCD(最大公约数 or 最大公因数)
因子:若b整除a,则说b是a的一个因子,用b|a 表示
-
-
- 若 a|1, 则a = ±1
- 若 a|b 且 b|c 则 a|c
- 若 a|b 且 b|a, 则 a = ± b
- 任何不等于0的数整除0
- 对于任意整数m, n,若有b|g, 且 b|h,则有b | (mg + nh)
- 若有b|g,则存在g1, 使得g可以表示为 g = b × g1
-
Euclid algorithm:
(1)假设我们要求出整数a 和 b 的最大公因子d,因为gcd(|a|, |b|) = gcd(a, b), 我们大胆假定 a ≥ b > 0
(2)使用带余除法,b除a表示为: a = q1b + r1 ; 0 ≤ r1 < b
(3)首先靠遇到 r1 = 0 时,即 b整数了a , 余数为0, 模运算 a mod b = 0, a 和 b 的公因子不可能有
比b更大的数了,所以这时候, 最大公约数 d = gcd(a, b) = b
(4)另一种情况是, r1 ≠ 0, 这时,由于存在 d|a, d|b, 那么一定有d | (a - q1b) 即: d|r1, d是r1的因子!
(5)考察gcd(b, r1) = ? 我们知道了
d|b , d|r1, 对于b 和 r1的任何一个公因子c来说,有c|(q1b + r1) 即 c|a, c|b,
我们说 c ≤ d, 因为 d 已经被定义为最大的的那个公因子,
所以 d = gcd(b, r1)
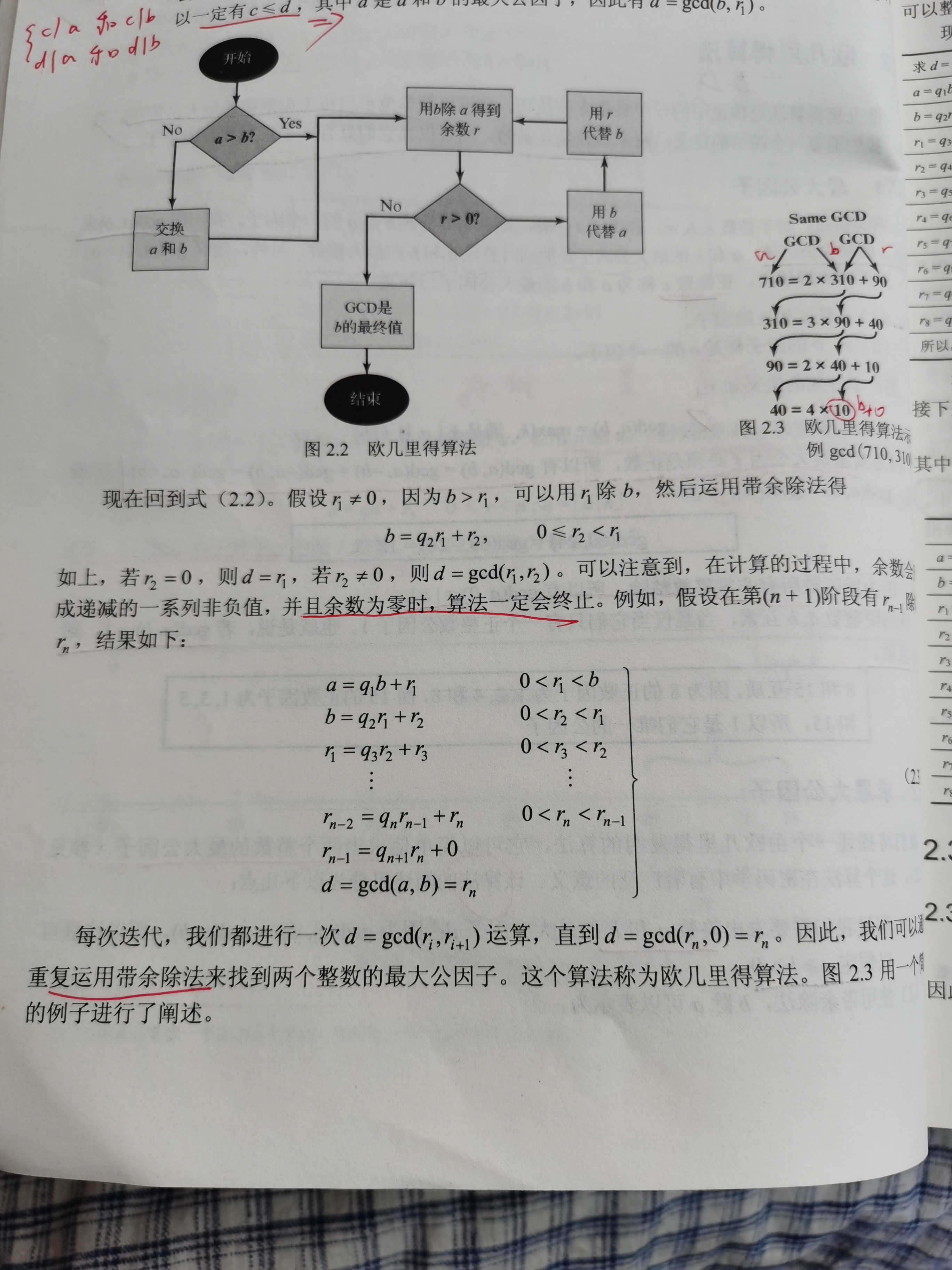
特别的,如果说gcd(a,b) = 1 ,那么就说a 和 b互质
Euclid 算法python实现:
>>> def mygcd(a, b): ... while a != 0: ... a, b = b % a, a ... return b >>> >>> mygcd(9, 3) 3 >>> mygcd(409119243, 87780243) 6837 >>>