转载请注明出处:http://www.cnblogs.com/Peyton-Li/
朴素贝叶斯法是机器学习模型中一个比较简单的模型,实现简单,比较常用。
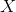 是定义在输入空间
是定义在输入空间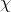 上的随机向量,
上的随机向量,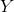 是定义在输出空间
是定义在输出空间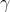 上的随机变量。
上的随机变量。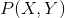 是
是 和
和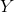 的联合概率分布。训练数据集
的联合概率分布。训练数据集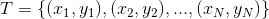 由
由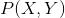 独立同分布产生。
独立同分布产生。
朴素贝叶斯法通过训练数据集学习联合概率分布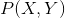 。具体地,学习一下先验概率分布及条件概率分布。
。具体地,学习一下先验概率分布及条件概率分布。
先验概率分布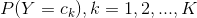 ,条件概率分布
,条件概率分布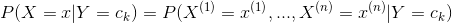 ,
,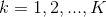 ,于是学习到联合概率分布
,于是学习到联合概率分布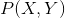 。
。
条件概率分布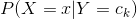 有指数级数量的参数,其估计实际是不可行的。事实上,假设
有指数级数量的参数,其估计实际是不可行的。事实上,假设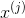 可取值有
可取值有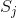 个,
个,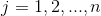 ,
, 可取值有
可取值有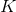 个,那么参数个数为
个,那么参数个数为 。
。
朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设,朴素贝叶斯法也由此得名。具体的,条件独立性假设是
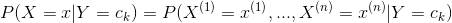
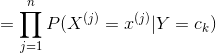 (4.3)
(4.3)
朴素贝叶斯法实际上学习到生成数据的机制,所以属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
朴素贝叶斯法分类时,对给定的输入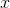 ,通过学习得到的模型计算后验概率分布
,通过学习得到的模型计算后验概率分布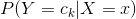 ,将后验概率最大的类作为
,将后验概率最大的类作为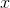 的类输出。后验概率计算根据贝叶斯定理进行:
的类输出。后验概率计算根据贝叶斯定理进行:
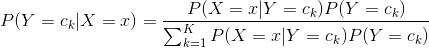 (4.4)
(4.4)
将式(4.3)带入(4.4)有
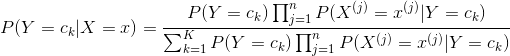 (4.5)
(4.5)
这是朴素贝叶斯法分类的基本公式。于是,朴素贝叶斯分类器可表示为
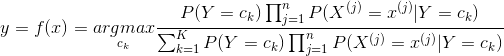 (4.6)
(4.6)
注意到,在式(4.6)中分母对所有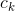 都是相同的,所以,
都是相同的,所以,
 (4.7)
(4.7)
朴素贝叶斯法将实例分到后验概率最大的类中。这等价于期望风险最小化。假设选择0-1损失函数:
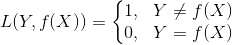
式中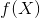 是分类决策函数。这时,期望风险函数为
是分类决策函数。这时,期望风险函数为
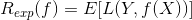
期望是对联合分布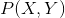 取的。由此取条件期望
取的。由此取条件期望
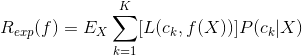
为了使期望风险最小化,只需对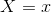 逐个极小化,由此得到:
逐个极小化,由此得到:

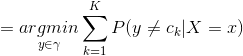
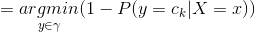
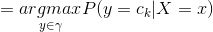
这样一来,根据期望风险最小化准则就得到了后验概率最大化准则:
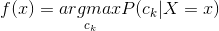 (4.8)
(4.8)
即朴素贝叶斯法所采用的原理。(注意将4.7式和4.8式对比)
在朴素贝叶斯法中,学习意味着估计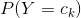 和
和 。可以应用极大似然估计法估计相应的概率。先验概率
。可以应用极大似然估计法估计相应的概率。先验概率 的极大似然估计是
的极大似然估计是
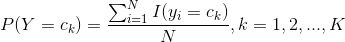
设第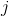 个特征
个特征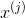 可能取值的集合为
可能取值的集合为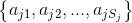 ,条件概率
,条件概率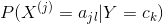 的极大似然估计是
的极大似然估计是

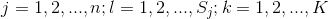
式中,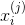 是第
是第 个样本的第
个样本的第 个特征;
个特征;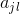 是第
是第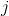 个特征可能取的第
个特征可能取的第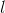 个值;
个值; 为指示函数。
为指示函数。
对于给定的实例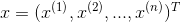 ,计算
,计算
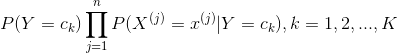
确定实例 的类
的类

用极大似然估计可能会出现所要估计的概率值为0的情况。这是会影响到后验概率的计算结果,使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。具体地,条件概率的贝叶斯估计是
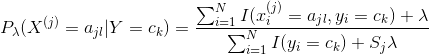 (4.10)
(4.10)
式中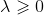 。等价于在随机变量各个取值的频数上赋予一个正数
。等价于在随机变量各个取值的频数上赋予一个正数 。当
。当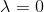 时就是极大似然估计。常取
时就是极大似然估计。常取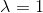 ,这是称为拉普拉斯平滑(Laplace smoothing)。显然,对任何
,这是称为拉普拉斯平滑(Laplace smoothing)。显然,对任何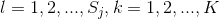 ,有
,有
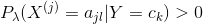
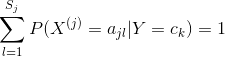
表明式(4.10)确为一种概率分布。同样,先验概率的贝叶斯估计是
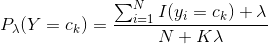
朴素贝叶斯分类有一个限制条件,就是特征属性必须有条件独立或基本独立(实际上在现实应用中几乎不可能做到完全独立)。
优点:
1、朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2、对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
3、对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点:
1、理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2、需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3、由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。对输入数据的表达形式很敏感。