【链表】怎么判断链表有环，怎么找环节点

思路（证明有环）：

定义快慢指针fast和slow，fast每次前进两步，slow每次前进一步；

当fast和slow在到达链尾之前相遇的话，就证明有环（类似于在操场上跑步跑的慢的被快的套圈但总会遇到）；

思路（找环结点）：

fast和slow相遇之后，fast不动，slow回到最初的起点，然后一步一步的等在再次相遇，这时候相遇地点就是环结点

证明如下，是个数学问题。。。

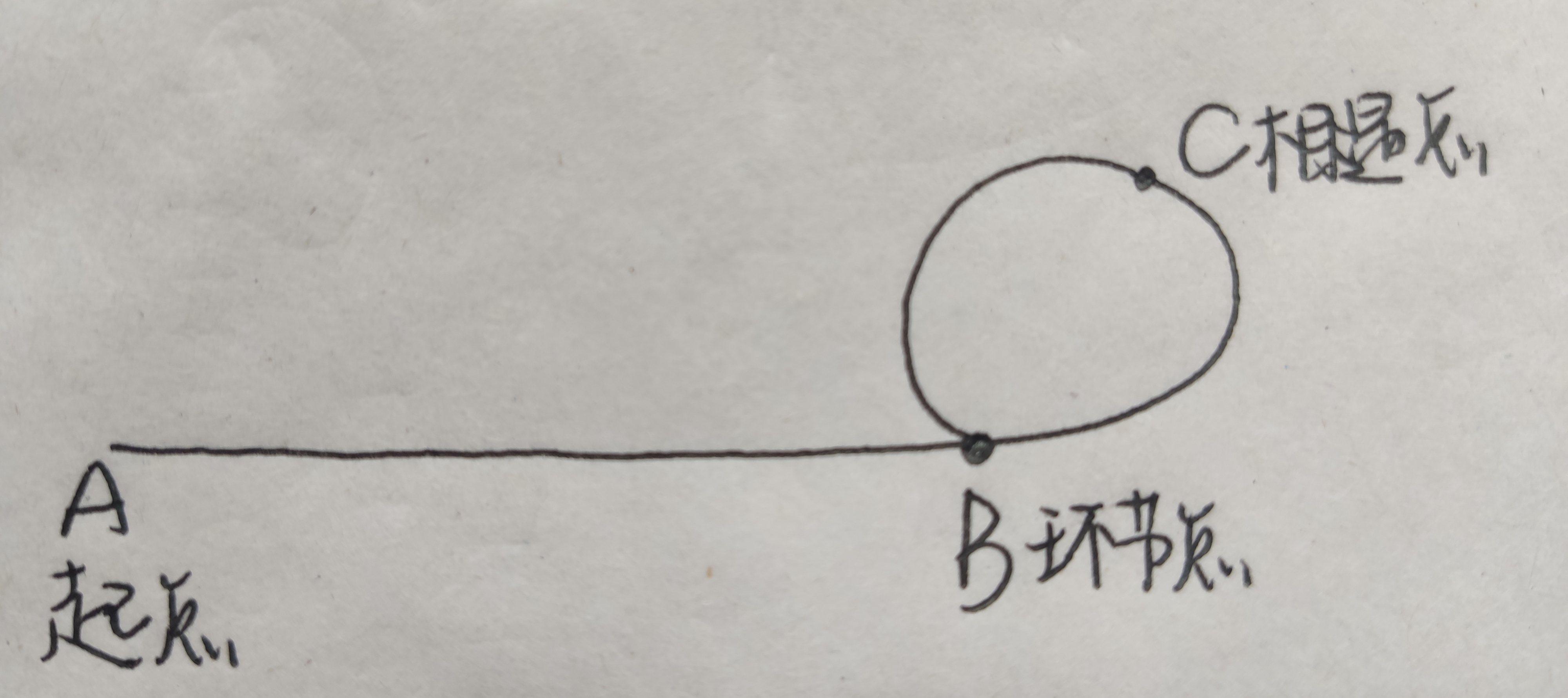
设一环的距离是R，k代表环数

slow走过的距离：AB+BC

fast走过的距离：AB+BC+k*R

因为slow每次一步，fast每次两步，所以距离有两倍关系

2（AB+BC）=AB+BC+k*R

AB+BC=(k-1)*R+BC+CB

AB=(k-1)*R+CB

所以结论就是fast从C->B加k圈停在B的时候，slow正好从A->B到达B

#include <iostream>
using namespace std;

typedef struct ListNode* List;
struct ListNode {
    int data;
    List next;
};

List judge(List L) {
    if (L == NULL || L->next == NULL)
        return NULL;
    List fast = L;//定义快指针
    List slow = L;//定义慢指针
    while (fast->next->next != NULL &&fast->next!=NULL) {
        fast = fast->next->next;
        slow = slow->next;
        //如果指针相遇跳出循环
        if (fast == slow)
            break;
    }
    //如果到头也没有找到证明没有环
    if (fast->next == NULL || fast->next->next == NULL)
        return NULL;

    //此时fast记录相遇点，slow回到头指针
    slow = L;
    while (fast != slow) {
        fast = fast->next;
        slow = slow->next;
    }
    //再次相遇的结点就是环结点
    return slow;
}

思路参考https://segmentfault.com/a/1190000015308120