【问题描述】
(由于是英文的,看不懂,这里就把大意给大家说一下吧……都是中国人,相信大家也不愿意看英文……)
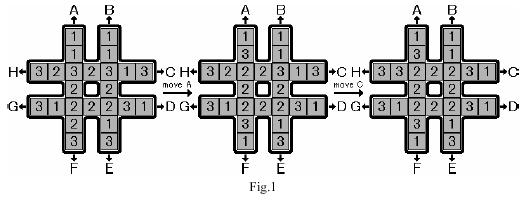
如图,一个井字形的棋盘,中间有着1-3任意的数,有ABCDEFGH八个操作,每个操作意味着该操作所在行朝该操作方向整体移动一格,详见图,你的目的是:对于输入的多组数据,用最少的步数使得井字形棋盘中间的八个数为同一个数,若不需操作就已达到要求,则输出“No moves needed”,无论是否需要操作,你都应将中间的数字给输出。输入以一个0结束。
【样例输入】
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
【样例输出】
AC
2
DDHH
2
【解题思路】
又是一道求最少步数的题目……果断写广搜,然而,写完广搜后,我奇迹般地发现……MLE了…………………………空间只给了150MB,我再一看时间………………15000ms……也不想多说什么了,赶紧用上今天刚学的IDA*算法。
IDA*算法是一种将估价函数与深搜结合的搜索方法,搜索方式是用深度优先搜索的方式,搜完第k层若还没有结果,那么就退出,然后从第一层开始搜到第k+1层,不断加深所搜的层数,因此又叫迭代加深搜索。其实说这么复杂,按我的理解,就是用深搜来做的广搜……
现在我们来看一下题目。因为是井字型棋盘,且输入还是一行数,那么,我们就给棋盘上的数标上号,分别为1-24,那么八个移动的过程也可以表示出来了,然后由于是深搜,那么就还有回溯的过程,对于每一个操作,都需要一个反操作,而题目中正好又提示了我们,A的反操作是F等等,因此,我们只需要记录每个操作的反操作是第几个就行了。
然后是边界条件,这里的边界条件是当搜索层数大于当前所设置的最大深度限制时,便退出,实际上每一个迭代加深搜索都有这个边界条件,而另外的边界条件则因题目而异,这道题则不需要其他的边界条件,满足要求退出即可。
接下来考虑初始化的问题,我们在找中间的值的时候,自然是要找最多的数,然后将其他的数移成这个数就行了,那么估价函数就是8-最大的数的个数,从这个估价函数的层数开始搜索,详见代码。
【代码实现】
1 const xh:array[1..8,1..7] of longint=((1,3,7,12,16,21,23),(2,4,9,13,18,22,24),(11,10,9,8,7,6,5),(20,19,18,17,16,15,14),(24,22,18,13,9,4,2),(23,21,16,12,7,3,1),(14,15,16,17,18,19,20),(5,6,7,8,9,10,11)); 2 fan:array[1..8] of longint=(6,5,8,7,2,1,4,3); 3 op:array[1..8] of char=('A','B','C','D','E','F','G','H'); 4 mid:array[1..8] of longint=(7,8,9,12,13,16,17,18); 5 var n,m,dep:longint; 6 s:array[1..24] of longint; 7 a:array[1..50] of longint; 8 i,j:longint; 9 function max(a,b,c:longint):longint; 10 begin 11 max:=a; 12 if b>max then 13 max:=b; 14 if c>max then 15 max:=c; 16 end; 17 function get:longint; 18 var i:longint; 19 cnt:array[1..4] of longint; 20 begin 21 fillchar(cnt,sizeof(cnt),0); 22 for i:=1 to 8 do 23 inc(cnt[s[mid[i]]]); 24 exit(8-max(cnt[1],cnt[2],cnt[3])); 25 end; 26 procedure move(k:longint); 27 var i,t:longint; 28 begin 29 t:=s[xh[k,1]]; 30 for i:=1 to 6 do 31 s[xh[k,i]]:=s[xh[k,i+1]]; 32 s[xh[k,7]]:=t; 33 end; 34 function dfs(k:longint):boolean; 35 var i,h:longint; 36 begin 37 if k>=dep then 38 exit(false); 39 for i:=1 to 8 do 40 begin 41 move(i);//移动 42 a[k]:=i; 43 h:=get;//求最多的数的个数 44 if h=0 then exit(true); 45 if (k+h<dep)and(dfs(k+1)) then//深搜 46 exit(true); 47 move(fan[i]);//回溯 48 end; 49 exit(false); 50 end; 51 begin 52 read(s[1]); 53 while s[1]<>0 do 54 begin 55 for i:=2 to 24 do 56 read(s[i]); 57 dep:=get; 58 if dep=0 then 59 begin 60 writeln('No moves needed');//所给数据本就满足要求,输出,退出 61 writeln(s[7]); 62 read(s[1]); 63 continue; 64 end; 65 while not(dfs(1)) do//如果不满足要求,加深层数,再进行深搜 66 inc(dep); 67 for i:=1 to dep-1 do 68 write(op[a[i]]); 69 writeln; 70 writeln(s[7]); 71 read(s[1]); 72 end; 73 end.