前言：
摘抄自wiki的关于仿射变换的定义：
http://zh.wikipedia.org/wiki/%E4%BB%BF%E5%B0%84%E5%8F%98%E6%8D%A2
仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。
一个对向量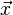
平移
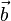，与旋转放大缩小
的仿射映射为
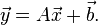【1】
1、移位加密：
比方说：把字母表全部向右循环移1位，也就是A变成B，B变成C，... ， Z变成A。
用数学一点的术语我觉得所谓“移位”就是映射吧。
那么我们可以写出通解公式，——现在是已知明文和加密步骤，进行加密，也就是求密文。
New = (Old + k) (mod table) 【2】
注释：
New：要求的密文
Old ：明文
k ：移位的位数
table：这张表有多大，比方说字母表就是26个字母，table就是26.
2、仿射变换：
移位加密和仿射变换有啥关系呢？
额 ，因为移位加密就是一种放射变换。。。
首先我们在1里面的变量命名现在改一下，以便更好地认识，变成：
y = (x + b)(mod m) 【3】
是不是和【1】很像啦，可惜我们的x没有系数。。
但是没关系，我们完全可以自己加上一个系数，把【3】变成：
y = (ax + b)(mod m) a,b为整数； 【4】
这样已经很像了，只不过【1】里面的自变量是向量。
但是，我们这里讨论的是一维的变换，所以不用用到2维及其以上的向量。（一维数字标记的向量就是普通的数嘛……）
3、知道了1、2这些，我们现在的目标就是——
"当知道一个一维的仿射变换的加密，
a. 怎么把明文加密
b. 怎么把密文解密 "
对于"a. 怎么把明文加密"，我们已经解决了，就是【4】那个公式。
对于"b. 怎么把密文解密"嘛，其实也不复杂。待我不快不慢地说来。
首先由【4】我们可以得到什么？
没错！就是 y ≡ (ax + b)(mod m) —— 这是明显的事实不用证明了。
然后正视一下题目是什么：我们现在已知a,b,y,m，要求x。
1). 左右移位一下 ,变为 y-b ≡ (ax)(mod m) 【5】
{为啥【5】是对的？
首先同余式可以相加，
即 若 a ≡ b (mod m), c ≡ d (mod m)， 【*】
那么(a + c) ≡ (b + d)(mod m) .
——同余式可以相加的证明用同余的定义就好……
然后 y ≡ (ax + b)(mod m)
-b ≡ -b (mod m)
所以……
}
2). 已知y-b ≡ (ax)(mod m)，x未知，求x.
现在已知ax ≡(y-b) (mod m)；
{首先我们要知道 同余式可以相乘，若【*】，则 ac ≡ bd (mod m) .证明同样可以基于同余定义。}
这时候我们就脑补了，如果有一个c能使得 cax ≡ x ≡ c(y-b) (mod m)就好了！
也就是说这个c如果能使得ca = 1或者 更宽一点的：ca ≡ 1(mod m).那么就解决了！
3). 于是问题变成了：找一个c使得，ca ≡ 1(mod m)
于是很容易联系到费马小定理、欧拉定理一类的。
但是费马小定理要求m一定要是素数，这样和我们题目不符。
所以看看欧拉定理，对 gcd(a,m) = 1(m>1)，有aΦ(m) ≡ 1 (mod m)
{Φ(m) 为欧拉函数，就是小于等于m的与m互素的正整数个数。如Φ(2) = 1 ，Φ(6) = 2——6与{1,5}互素。}
所以如果ca = aΦ(m) ，那么就有ca ≡ 1(mod m)。
于是c = aΦ(m)-1 . 但是gcd(a,m) = 1，这一点不能漏。
4、综上，我们发现了，当c = aΦ(m)-1 时 ；
cax ≡c(y-b) (mod m)
化为 x ≡c(y-b) (mod m) {现在要附加gcd(a,m)=1这个条件了！}
5、那么对于仿射变换，
我们知道变化规则[即位移b]后，如何把密文[y]翻译成明文[x]呢？
结论是：
step 1. 求 c = aΦ(m)-1
step 2. x ≡c(y-b) (mod m)
番外小剧场：
窝：你在2里面为啥要改名字？该问题纯属好奇！
big窝：此中原因有2——
1. 如文中所说，为了更直观地比较。
2. 也是最根本的原因——变量命名如此之平凡，根本不是我的feel！OK？
窝：......
窝：第二个问题——你怎么知道同余式符合相加相乘原理？你怎么想到的？
big窝： 首先"同余式符合相加相乘原理"这个结论在数论里就像是实数有相加相乘的运算一样自然，如果想不到那么你需要找一本数论的书看看，不需要看完这就足以变成你的常识。至于怎么想到的，如果给你一堆数，你能想到的最基本的运算就是做加减乘除了吧？
窝：恩……好像是的……
big窝：那不就得了，说了同余式符合相加相乘原理是同余式的基本运算。
窝：……哦……