【Tarjan】缩点
在一个点N数据极大的图中,直接SPFA或者记忆花搜索时间超限,那么我们可以利用Tarjan缩点来减少N。
举个例子;
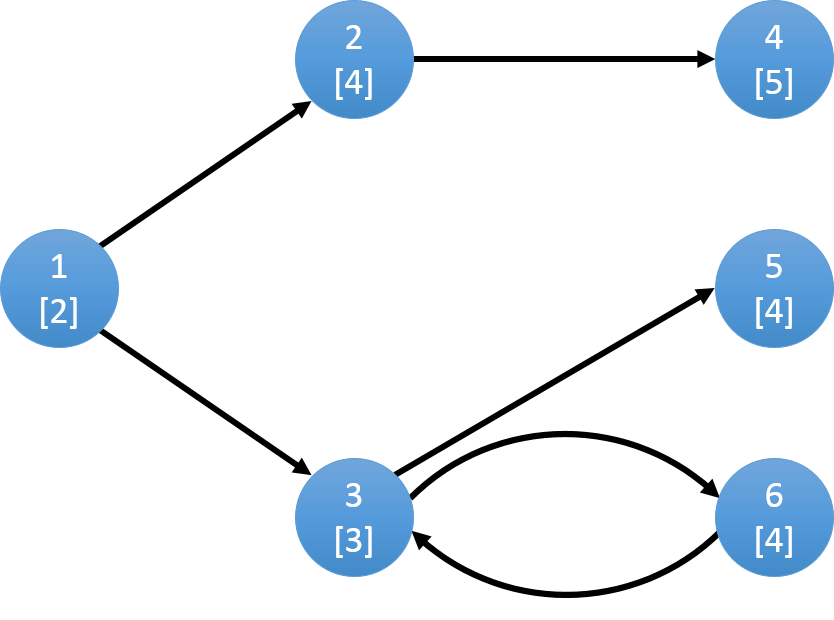
如上图:3,6两点为该图中的强连通分量,我们可以将它们看做一个单元点。
怎么缩点呢
我们使用fa[]数组来存每个点所在的强连通分量中时间戳(DFN)最小的点,即将该点设为单元点。
怎么连边
如果两个点的fa[]不一样,且该两点间有一条有向边,那么我们就把他们的单元点(即fa[])连一条边
问题的求解
缩点后,重新建图,我们先找出图中入度为0的点,使用SPFA或拓扑排序来求解问题,与最短路问题相似
P3387 【模板】缩点
代码如下:
#include<bits/stdc++.h>
using namespace std;
struct edge{
int nw,nxt,mark;
}pre[100010];
int n,m,idx,cnt;
int dfn[10010],low[10010];
int in[10010],v[10010],fa[10010];
int head[10010];
bool used[10010];
int stk[10010],p;
int ans=0;
void add (int x,int y,int cnt)
{
pre[cnt].nw=x;
pre[cnt].mark=head[x];
pre[cnt].nxt=y;
head[x]=cnt;
}
void tarjan (int u)
{
dfn[u]=low[u]=++idx;
stk[++p]=u;
used[u]=1;
for (int i=head[u];i!=0;i=pre[i].mark)
{
int nx=pre[i].nxt;
if (!dfn[nx])
{
tarjan (nx);
low[u]=min (low[u],low[nx]);
}
else if (used[nx])
low[u]=min (low[u],dfn[nx]);
}
if (low[u]==dfn[u])
{
do{
v[u]+=v[stk[p]];
fa[stk[p]]=u;
used[stk[p]]=0;
p--;
}while (stk[p+1]!=u);
v[u]>>=1;
}
}
int topo ()
{
int dis[10010];
queue<int>q;
for (int i=1;i<=n;i++)
if (fa[i]==i)
{
dis[i]=v[i];
if (!in[i])
q.push(i);
}
while (!q.empty())
{
int Now=q.front();
for (int i=head[Now];i!=0;i=pre[i].mark)
{
int Nxt=pre[i].nxt;
dis[Nxt]=max (dis[Nxt],dis[Now]+v[Nxt]);
in[Nxt]--;
if (!in[Nxt])
q.push (Nxt);
}
q.pop();
}
int maxx=0;
for (int i=1;i<=n;i++)
if (fa[i]==i)
maxx=max (maxx,dis[i]);
return maxx;
}
int main()
{
memset (in,0,sizeof (in));
memset (used,0,sizeof (used));
memset (dfn,0,sizeof(dfn));
memset (head,0,sizeof (head));
scanf ("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf ("%d",&v[i]);
for (int i=1;i<=m;i++)
{
int a,b;
scanf ("%d%d",&a,&b);
add (a,b,i);
}
for (int i=1;i<=n;i++)
if (!dfn[i])
tarjan (i);
memset (head,0,sizeof (head));
for (int i=1;i<=m;i++)
{
int Now=fa[pre[i].nw];
int Nxt=fa[pre[i].nxt];
if (Now!=Nxt)
{
add (Now,Nxt,++cnt);
in[Nxt]++;
}
}
printf ("%d",topo ());
return 0;
}