·题目:
如何福慧双修?被太后教导的甄嬛徘徊在御花园当中。突然,她发现御花园中的花朵全都是红色和蓝色的。她冥冥之中得到了响应:这就是指导她如何福慧双修的!现在御花园可以看作是有N块区域,M条小路,两块区域之间可通过小路连接起来。现在甄嬛站在1号区域,而她需要在御花园中绕一绕,且至少经过1个非1号区域的区域。但是恰好1号区域离碎玉轩最近,因此她最后还是要回到1号区域。由于太后教导她要福慧双修,因此,甄嬛不能走过任何一条她曾经走过的路。但是,御花园中来往的奴才们太多了,而且奴才们前行的方向也不一样,因此甄嬛在走某条小路的时候,方向不同所花的时间不一定一样。天色快暗了,甄嬛需要尽快知道至少需要花多少时间才能学会如何福慧双修。如果甄嬛无法达到目的,输出“-1”。
输入格式:
第一行仅2个正整数n,m,意义如题。
接下来m行每行4个正整数s,t,v,w,其中s,t为小路所连接的两个区域的编号,v为甄嬛从s到t所需的时间,w为甄嬛从t到s所需的时间。数据保证无重边。
输出格式:
仅一行,为甄嬛回到1号区域所需的最短时间,若方案不存在,则输出-1
样例输入:
样例一
3 3
1 2 2 3
2 3 1 4
3 1 5 2
样例二
3 2
1 2 1 1
2 3 1 2
样例输出:
样例一 8
样例二 -1
数据范围:
对于40%的数据:n<=1,000; m<=5,000
对于100%的数据:1<=n<=40,000; 1<=m<=100,000; 1<=v,w<=1,000
·花哨题目,述大意:
输入一张图,两点之间的成对的有向边权值不同(保证无重边),求出从1号点出发,并不走重复的路回到1号点的最短路长度。边权大于0。
·分析:
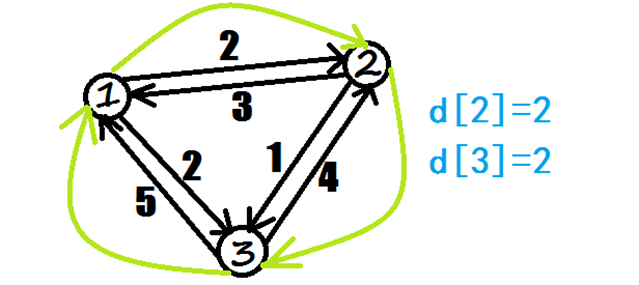
首先第一个发现的问题是,其实这不算是我们常用的单源点最短路:由于不能走重复的路径,那么普通的最短路更新方式会出现问题——由于只有到某一点的距离小于以前的d[]值,才会更新,如果遇上走过的边,那么就回不到1点,即程序无法找到一条关于i的回路,即使它存在。如图:
如图,正确的答案路径是:[1->2->3]。但根据最短路算法,我们发现2,3两个点最小d值都是由1更新而来。我们的愿望是让2能够更新3,3来更新1从而组成回路,得到答案。但这个图足以证明照搬最短路算法不加以条件限制得出的答案是不准确甚至错误的。
那么我们怎么防止走相同的路呢?一旦有办法保证,再进行最短路,或许可以更新得到正确答案。这样思考的原因是要尝试将原图做一些处理或者限制,使得最短路算法能够正确进行。由于边权为正,而且d[1]=0,所以只有在扩展时遇到v==1,就加以特判,更新答案。但这样带来了问题,一个是上文图片所示的最短路不满足的问题,另一个问题是重复走过一条边(这两个问题的关系是,如果要满足最短路,就可能会重复走一条边)。由于只是在再次到达1点时加以特判,所以我们只需要避免与1有关的边不重复走就是了。
怎么阻止重复走关于1的一条边?一种很简单的思想是,将每条(u,v)作为最短路的出边(强制规定,在最短路开始前就q.push(v)),并在更新到1的答案时禁止使用这一条边。
但是直接枚举每一条边,进行最短路,时间不能承受。优化办法如下:
·第一种处理方式——二进制分组:
本题的点数n<=40000,那么二进制位数小于14位。因为我们防止走重复的边的一种途径就是找到这两个点的不同之处——毫无疑问,不同的数的二进制数总存在一位不同,那么1的出边我们定为二进制某一位为1,我们就尝试只从这一位为0的点(边)回到1。这样一来只需进行28次(翻倍干嘛?)最短路,考试的数据可以AC(每个测试点最高耗时600ms左右,总共耗时在1600ms左右)。美丽的代码:
1 #include<queue>
2 #include<stdio.h>
3 #include<cstring>
4 #define go(i,a,b) for(int i=a;i<=b;i++)
5 #define mem(c,a,b,l) memset(a,b,sizeof(c)*(l+1))
6 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
7 const int N=40003;
8 using namespace std;
9 struct E{int v,next,w;}e[N*10];
10 int n,m,head[N],k=1,d[N],ans=1e9,_=1;bool inq[N];
11 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;}
12 void SPFA(int A,int B)
13 {
14 mem(int,d,0x7f,n);mem(bool,inq,0,n);
15 queue<int>q;fo(i,head,1)if((v&A)==B)
16 q.push(v),inq[v]=1,d[v]=e[i].w;
17 int u;while(!q.empty())
18 {
19 inq[u=q.front()]=0;q.pop();
20 fo(i,head,u)
21 {
22 if(v==1&&(u&A)!=B)ans=min(ans,d[u]+e[i].w);
23 if(v!=1&&d[u]+e[i].w<d[v])d[v]=d[u]+e[i].w,
24 !inq[v]?q.push(v),inq[v]=1:1;
25 }
26 }
27 }
28 int main()
29 {
30 scanf("%d%d",&n,&m);go(i,1,m){int u,v,w1,w2;
31 scanf("%d%d%d%d",&u,&v,&w1,&w2);ADD(u,v,w1);ADD(v,u,w2);}
32 while(_<=n)SPFA(_,_),SPFA(_,0), _<<=1;
33 printf("%d",ans);return 0;
34 }//Paul_Guderian
·第二种处理方式——重新建图:
上文方法实际上效率并不高,因为做了许多重复的工作。我们尝试不做或者少做这些重复工作,争取一次或者两次SPFA就可以完成。值得注意的是,这道题我们一直是在提防(1,v)这样的边重复走,所以我们试试构建新图来抹去这样纠结的关系。
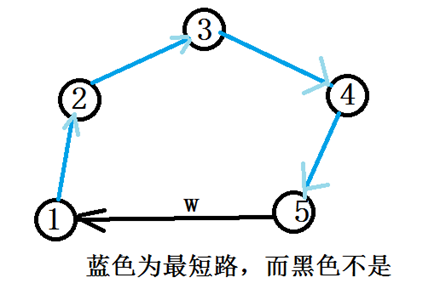
一个绝妙的理解:对于每一个关于1的环(回路),我们可以将它看作是一些“最短路片段”和一些非最优的边权组成的,例如:
再次到达1的路径可以由一条到5的最短路和边w组成。我们考虑最短路拼接的目的是提高路径寻找效率,然后带着防止重复走的思想,设d[u]表示预先进行一遍以1为源点的最短路每个点的最短路长度,使用pre[u]表示关于u的最短路从1出发后到达的第一个点的标号,并且为了区分1,我们使用n+1号点表示1作为终点时点,做出如下新图构建的讨论:
[1]对于有向边(1,v,w):
如果pre[v]==v:直接忽略这个边①
如果pre[v] !=v:在新图中添加边(1,v,w)②
[2]对于有向边(u,1,w):
如果pre[u]==u:在新图中添加边(u,n+1,w)③
如果pre[u] !=u:在新图中添加边(1,n+1,d[u]+w)④
[3]对于除上文的其他边(u,v,w):
如果pre[u]==pre[v]:在新图中添加边(u,v,w)⑤
如果pre[u] !=pre[v]:在新图中添加边(1,v,d[u]+w)⑥
上文其实只是直接给出了结论。但是有一个总体感觉是,故意绕开最短路建边。慢慢地分析:首先,必须清楚的是①③是一个“套餐”,前者保证不会从那里出去就马上回来,后者保证其他地方而来的可以直接使用这一条边更新答案。然后,可能有一个误区是①操作是否阻断了从v出发的情况——没有,因为它至少需要走两步才能不会乱更新答案,所以它的贡献体现在[3]中的新边构建中了。其余部分表示的内容就很清晰了,无非是利用原来的最短路信息建边,实质上是弥补最短路的不足(例如不足体现在本文开头的那个反例图片中)。
因此,这个方法的步骤是:首先进行一遍最短路算法预处理出d和pre数组,然后根据上文结论构建新图,再进行一次最短路算法。接下来的这一份代码总时间都才花费200ms左右(因为只有两次最短路)。
1 #include<queue>
2 #include<stdio.h>
3 #include<cstring>
4 #define go(i,a,b) for(int i=a;i<=b;i++)
5 #define fo(i,a,x) for(int i=a[x],v=e[i].v;~i;i=e[i].next,v=e[i].v)
6 #define mem(a,b) memset(a,b,sizeof(a))
7 using namespace std;const int N=40003;
8 int n,m,head[N],Head[N],k,d[N],pre[N],_=1;
9 struct E{int v,next,w;}e[N*10];bool inq[N];
10 void ADD(int u,int v,int w,int *H){e[k]=(E){v,H[u],w};H[u]=k++;}
11 void SPFA(int *H)
12 {
13 queue<int>q;go(i,1,n+1)d[i]=1e9+4,inq[i]=0;d[1]=0;
14 if(_)fo(i,H,1)d[v]=e[i].w,inq[v]=1,pre[v]=v,q.push(v);
15 else q.push(1);int u;while(!q.empty())
16 {
17 inq[u=q.front()]=0;q.pop();fo(i,H,u)if(e[i].w+d[u]<d[v])
18 d[v]=d[u]+e[i].w,pre[v]=pre[u],!inq[v]?q.push(v),inq[v]=1:1;
19 }
20 }
21 int main()
22 {
23 freopen("in.in","r",stdin);
24 mem(head,-1);mem(Head,-1);scanf("%d%d",&n,&m);
25 go(i,1,m)
26 {
27 int u,v,w1,w2;
28 scanf("%d%d%d%d",&u,&v,&w1,&w2);
29 ADD(u,v,w1,head);ADD(v,u,w2,head);
30 }
31 SPFA(head);_=0;
32 fo(i,head,1)
33 {
34 if(pre[v]!=v)ADD(1,v,e[i].w,Head);
35 if(pre[v]==v)ADD(v,n+1,e[i^1].w,Head);
36 if(pre[v]!=v)ADD(1,n+1,e[i^1].w+d[v],Head);
37 }
38 go(u,2,n)fo(i,head,u)if(v!=1)
39 {
40 if(pre[u]==pre[v])ADD(u,v,e[i].w,Head);
41 if(pre[u]!=pre[v])ADD(1,v,e[i].w+d[u],Head);
42 }
43 SPFA(Head);printf("%d",d[n+1]);return 0;
44 }//Paul_Guderian
低保金发到工厂细雨落到窗前,
隐秘的子弹穿过虚空嵌入胸膛。——汪峰《哭泣的拳头》