【线性筛】

在这里提供三种线性筛的讲解,它们分别是:素数筛,欧拉筛和莫比乌斯筛。

 

·筛法正确性的重要理论依据：

上述函数均为积性函数。积性函数的性质为:若f(x)是一个积性函数,那么对于任意素数a,b,满足f(ab)=f(a)*f(b)

 

·一些可爱的要点(有助于理解筛法原理)：

    ①欧拉筛和莫比乌斯筛是以素数筛为基础的。

    ②三者在代码实现上几乎是同一框架。

    ③欧拉函数和莫比乌斯函数的定义介绍：

    (1)欧拉函数Phi(x)表示小于等于x的正整数中和x互质的数的个数(注意,1与任何数互质)。

     (2)莫比乌斯函数Mob(x)仅有三种值:0,-1,1————如果x能够被一个大于0的整数的平方整除，那么函数值为0;如果x拥有奇数种 质因数，那么函数值为-1，有偶数种质因数，那么函数值为1(莫比乌斯函数的神奇定义决定了它应用于容斥问题......)。

 

·线性筛的两大步骤：

      (1)获得范围内的素数

      线性筛的线性体现在尽可能的使每个数只被“筛”一次。其思想众所周知地基于： a为任何数,b为质数,那么a*b就不是质数。

     在程序实现中体现为，对于当前枚举的数i,使用所有小于等于i的素数p，去“筛除”数(p * i),即将布尔数组对应位置设为1(表示不为素数)。

      值得注意的是，这里会出现三个筛法都会 涉及的关键语句：“if(i%Prime[j]==0)break;”。这是一个很简单有效的优化，原理依旧是基于“尽量只筛一次”。

     下面对这个优化做出解释:在这里我们提出“最小质因子”的概念，然后我们规定每个合数都只被它的最小质因子筛出————这个定义很好地契合了“尽可能只筛一次”的想法。

     回到问题，当前如果出现"i%Prime[j]==0"的情况，由于枚举素数Prime[j]是从小到大的,那么可以说明Prime[j]是i的最小质因子。

     此时如果不终止循环，那么Prime[j+1],Prime[j+2]...会与i相乘得到结果然后筛掉这个结果，但是我们从式子中看出，得到的结果的最小质因子是Prime[j],然而我们使用了j之后的素数筛掉了它，不符合开始的原则，这样做 会使得一个数被筛多次，降低了效率。举例说明则是：20应该由2 * 10筛掉，而不是被4 * 5筛掉(素数2<素数5)。

然后这里就给出素数筛代码吧吧吧：

素数的线性筛

 

(2)正式开筛

(一)欧拉函数的线性筛

首先给出欧拉函数的定义式子：(p表示x的质因数)

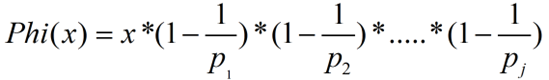
对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）

然后考虑如何用类似于筛素数的方法筛出欧拉函数。

类似于素数,可以做出如下分类讨论：(设p为素数)
     ①Phi(p)=p-1

     ②若已知Phi(x),且p能整除x: Phi(x*p)=Phi(x)*p

     ③若已知Phi(x),且p不能整除x：Phi(x*p)=Phi(x)*(p-1)

简单地证明上述式子：对于①,由于p本身是一个素数，那么比它小的所有数都和它互质，因此答案为p-1。对于②,p已经是x的质因子,因此我们看看欧拉函数的定义式可以的出括号相乘部分不会改变,只会把最前面的x变成x*p。对于③,p是新加入的质因子,相当于式子前面多乘了个p,然后多加了一个括号，所以相当于原式多乘了: p*(1-1/p)即(p-1)。

    呆码在这里：
 

 

(二)莫比乌斯函数的线性筛

首先给出欧拉函数的定义式子：

 

我们在这里使用和上文筛欧拉函数类似的分类讨论: (设p为素数) ①μ(p)=-1 ②已知μ(x),且p能够整除x,则μ(x*p)=0 ③已知μ(x),且p不能够整除x,则μ(x*p)=-μ(x)三个结论的证明比上文的Euler要简单很多——只需要照着莫比乌斯函数的定义去讨论0,1,-1三种情况就是了。

·细节处理以及高效理解：

   (1)坚持"每个数尽量只被筛一次"的原则

     这里主要包含两点。第一，上述筛法依靠这个思想本身就已经很优秀了。第二，也就是上文提到的小优化：

            三个筛法都包含了这句话，为什么呢？因为这三种方法其实都是基于素数来进项筛数的，因此既然依靠素数，那么都可以要求每个数只能被最小质因数筛去而不能被其他质因子筛去，这样做到了每个数只被筛一次。这个细节值得被理解和记住。

(2)找找看，三种筛法的代码共同之处有哪些？啊，全在下面啦：

小伙伴们问在没有不熟练的情况下怎么记住模板，其实三种筛法模板是一样的，所以只需要记住素数模板和欧拉和莫比乌斯函数部分的分类讨论就是了。大米饼建议理解所有筛法，这才是最高效的。

·代码实现：

#include<stdio.h>
#define go(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
struct Sieve
{
    /*void XXX_Sieve()
    {
        XXX[1]=1;
        go(枚举所有数i)
        {
            if(没有被筛去)记录素数,XXX[i]=某个值;
            
            go(枚举小于等于i的素数)
            {
                if(结果超界)break;
                依据分类讨论计算XXX[i*prime[j]]的值。 
                if(i%Prime[j]==0)break;
            }
        }
    }*/
    static const int N=200003;
    
    bool NotPrime[N];
    int Prime[N],t;
    
    void Prime_Sieve()
    {
        NotPrime[1]=1;
        go(i,2,200000)
        {
            if(!NotPrime[i])Prime[++t]=i;    
                
            go(j,1,t)
            {
                if(1ll*Prime[j]*i>200000)break;
                NotPrime[Prime[j]*i]=1;
                if(i%Prime[j]==0)break;
            }
        }
    }
    
    int Phi[N];
    
    void Euler_Sieve()
    {
        t=0;Phi[1]=1;
        go(i,2,200000)
        {
            if(!NotPrime[i])t++,Phi[i]=i-1;    
            go(j,1,t)
            {
                if(1ll*Prime[j]*i>200000)break;
                Phi[i*Prime[j]]=Phi[i]*(i%Prime[j]?Prime[j]-1:Prime[j]);
                if(i%Prime[j]==0)break;
            }
        }    
    }
    
    int Mob[N];
    
    void Mobius_Sieve()
    {
        t=0;Mob[1]=1;
        go(i,2,200000)
        {
            if(!NotPrime[i])t++,Mob[i]=-1;
            
            go(j,1,t)
            {
                if(1ll*Prime[j]*i>200000)break;
                Mob[i*Prime[j]]=i%Prime[j]?-Mob[i]:0;
                if(i%Prime[j]==0)break;
            }
        }
    }
    
}Tool;

int main()
{
    Tool.Prime_Sieve();
    Tool.Euler_Sieve();
    Tool.Mobius_Sieve();
    return 0;
}//Paul_Guderian

大米飘香的总结：

      本文介绍了三种筛法,包括素数筛法和两个积性函数的筛法。线性筛本身并不能成为一道题，但是却是数论问题中常见的预处理，因此熟练掌握十分重要。如Mobius函数的预处理是解决Mobius-Inversion问题的基础。在结束了像筛法这样的重要基础的学习后，便可信心十足地奔赴曾经认为高深莫测的版块——数论了。祝你美妙。

                                                   

   

每当夜深人静的时候，望着那灿烂的夜空，

我会感到那里充满了，太多的梦想…… ——————汪峰《英雄》