先给出比赛地址啦,感觉这场比赛思维考察非常灵活而美妙。
A. Odds and Ends
·述大意:
输入n(n<=100)表示长度为n的序列,接下来输入这个序列。询问是否可以将序列划分成奇数个连续部分,使得每一部分满足:开头结尾是奇数,序列长度也是奇数。如果可以输出Yes否则输出No。
·分析:
我们发现这是一道与奇偶性有关的问题,因此尝试进行一些分类讨论来探求解法。序列需要满足什么特点才能满足题目要求呢?
第一个突破口是:"划分成奇数个序列,每个序列长度为奇数个",据此得出一个结论:序列元素总个数一定是奇数个,理由是奇数乘奇数依旧是奇数。
根据上述结论,我们就只需要讨论n为奇数的情况了。接下来我们要关注的是能否划分为奇数个序列,使得首尾元素都是奇数。不必要去思考怎样拆分,因为无论怎样拆,我们可以发现如果要输出yes,那么整个序列开头和结尾一定是奇数,然而整个序列是1个,也就是满足奇数个序列,所以只需要判断输入的序列首尾是否为奇数就可以了。
总结的说,这道题分类讨论的过程如下:
①n为偶数——直接输出No
②n为奇数:
(1)原序列开头结尾元素均为奇数————输出Yes
(2)开头或者结尾不为奇数———————输出No
1 #include<stdio.h> 2 int n,a[103],sum,m; 3 int main() 4 { 5 scanf("%d",&n);m=n; 6 while(n)scanf("%d",a+n),sum+=a[n],n--; 7 puts(!(m&1)||!(a[1]&1)||!(a[m]&1)?"No":"Yes");return 0; 8 }//Paul_Guderian
B. Tell Your World
·述大意:
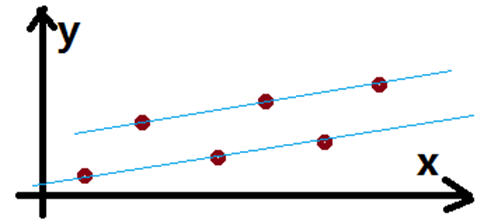
输入一个n(3<=n<=1000),然后输入n个点的坐标(xi,yi)(-109<=xi,yi<=109),第i个点的横坐标一定是i询问:是否存在两条不重合的平行线,能够经过所有点,并且每条线至少经过一个点。如果存在输出Yes否则输出No。
·分析:
注意'平行'这一的条件。为啥呢?因为我们如果确定了斜率,根据平行关系就可以得出两条线的斜率,然后就可以判断任何两点是否在直线上了。但是问题在于如何求出斜率,因为我们不知道哪两个点相连是正确的斜率。
得出关键结论:如果存在满足条件的斜率,该斜率一定会出现在前三个点互相连线得到的三个斜率之中。接下来我们只需要将三个斜率分别进行上述的验证,即看看是否能让所有点串在两条直线上且每条直线至少有一个点。
1 #include<stdio.h> 2 #include<math.h> 3 #define go(i,a,b) for(int i=a;i<=b;i++) 4 int n,t,cnt,tot,I,use[1003];double x[1003],y[1003],K[1003],k; 5 int main() 6 { 7 scanf("%d",&n); 8 go(i,1,n)x[i]=i,scanf("%lf",&y[i]); 9 go(i,1,2)go(j,i+1,3)K[++t]=(y[i]-y[j])/(x[i]-x[j]); 10 go(j,1,t) 11 { 12 k=K[j]; 13 go(i,1,n)use[i]=0;tot=cnt=use[1]=1; 14 go(i,2,n)if(fabs((y[i]-y[1])/(x[i]-x[1])-k)<1e-6)cnt+=(use[i]=1); 15 go(i,1,n)if(!use[i])I=i,i=n;if(cnt==n)continue; 16 go(i,I+1,n)if(fabs((y[i]-y[I])/(x[i]-x[I])-k)<1e-6)tot++; 17 if(!tot||tot+cnt<n)continue;puts("Yes");return 0; 18 } 19 puts("No");return 0; 20 }//Paul_Guderian
C. From Y to Y
述大意:
这是一道构造题。题目输入一个k(0 ≤ k ≤ 100 000)。要求我们构造一个小写字母可重集合,使得通过任意两个字符串(起初是一个字符)拼接形成新串的方式最终仅剩一个字符串(也就是集合所有元素组成的字符串)时的代价和为k。代价指的是每次串合并的时候对于每种字母在第一个串出现的次数乘上在第二个串出现的次数的和(就是把26种字母的加起来)。最后输出这个集合(可以重复,顺序任意)
分析:
这道题可能读题就难到了少许Oier…我们简化题意,发现合并顺序没有影响,所谓的代价其实就是每种字母之间形成二元组的个数的总和。写成式子就是:
∑(ai*(ai-1)/2)
(i表示第i中字母,ai表示在集合中的个数,'a'<=i<='z')
那么题目就转化为了一个类似于背包DP的问题:给出26种物品,每种物品可以选择无限多个,选择x个物品时能够获得价值x*(x-1)/2,求出一种物品购买方案,使得总价值等于k。
遗憾的是,虽然那样说,但是这道题背包DP是会TLE+MLE+QAQ的。回想以前学习背包之前第一次遇到背包问题就直接贪心做,尽量塞满就是了(当然这是错的),但是这道题的价值是"动态"的,物品的价值更加灵活,我们可以让贪心的方法重获新生!
先粗鲁地给出解法(因为还没证明,显得很不礼貌):
令sum(x)=x*(x-1)/2
从'a'开始,找到最大的x满足sum(x)<=k,然后就直接将x个当前字母压入答案中,并且k-=sum(x)。如果k还没有为0,就继续下一个字母进行相同操作,直到k为0跳出然后输出答案即可。
事后会问到,问什么这样做是合法的,因为根据以前的经验,贪心不一定是最优的。但别忘了以前的贪心思想里面有这样一条:先放大的,放不下了放小的。我们发现这道题的物品价值似乎可以满足:
sum(1)=0,sum(2)=1,sum(3)=3,sum(4)=6,sum(5)=10,sum(6)=15……
注意,我们只有26种物品。根据上文我们一股脑说出来的方法,26似乎不一定能够成功构造k。但我们观察这样一个细节:加入当前选择了5个'b',那么说明当前k<sum(6)-sum(5),也就是接下来的字母仅仅需要构造代价为k且满足k<sum(6)-sum(5)。
我们一般化上述结论:
对于当前字母能够取到最大的sum(i)时i取值为x,那么以后的字母需要构造使得代价等于k,此时k<sum(x+1)-sum(x)。
根据上述结论,发现每到下一个字母,k值的变化大致为:
sum(x) ————> sum(x+1)-sum(x)
展开:x*(x-1)/2 ———> x*(x+1)/2-x*(x-1)/2 (=x+1)
数量级角度: n2 ———> n
我们成功发现每次k值是开根级别的运算。计算发现就算是k最大100000也仅仅需要5次开根操作就接近1了。基于此,我们发现背包里添加较小物品来弥补剩下的空隙最多只会添加5次,更直观地说,按照上述构造方法其实字母种类不超过6个,因此不必担心用完物品的情况。
总结而言,此处巧妙使用了等差数列求和公式的性质,美妙至极。
1 #include<stdio.h> 2 #define sum(j) (j*(j-1)/2) 3 #define go(i,a,b) for(int i=a;i<=b;i++) 4 int main() 5 { 6 int k;scanf("%d",&k); 7 if(!k){puts("z");return 0;} 8 go(i,0,25){int j=2;while(k-sum(j)>=0)j++;j--; 9 go(t,1,j)printf("%c",'a'+i);if(!(k-=sum(j)))return 0;}return 0; 10 }//Paul_Guderian
D. Rooter's Song
·述大意:
输入n,w,h表示有n个舞蹈家,舞台x轴正方向上长为w,y轴正方向上长为y,舞蹈家有两种类型:一种是从y轴上一点(0,pi)出发,平行于x轴向x正半轴方向跳舞直到到达舞台边界;另一种是从x轴上一点(pi,0)出发,平行于y轴向y正半轴方向跳舞直到到达舞台边界。上述类型分别用1,2表示。接下来输入n个舞蹈家的信息(gi,pi,ti),gi表示类型,pi同上,ti表示表演开始后的ti时间该舞蹈家开始向指定方向移动。所有舞蹈家速度相同。如果不同类型的舞蹈家相遇,那么从y轴出发的舞蹈家的移动方向改变为平行于y轴的正半轴方向,从x轴出发的舞蹈家的移动方向改变为平行于x轴的正半轴方向,请按输入顺序输出每个舞蹈家最后的位置。相遇仅发生在两种不同类型的舞蹈家之间。
【官方样例解释】
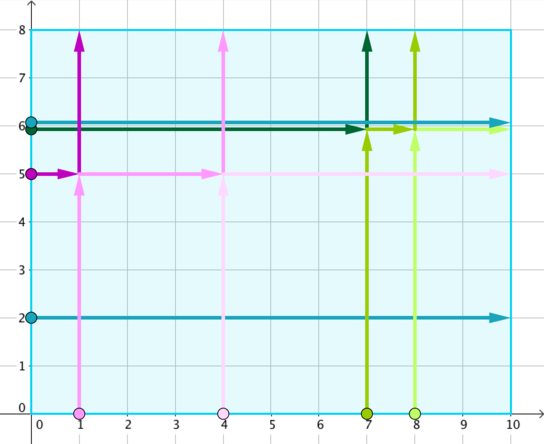
·分析:
最奇妙的是两人相遇……我们可以发现最终位置是不变的,只是到达那里的人变了。得出这个结论后,我们就只需要将每个人分配到这些位置上就可以了。此题关键在于如何为一个人找到正确的最终位置:
第一个突破口:几个人只有相遇后才会交换最终位置,而且是他们内部交换。也就是说不考虑相遇,每个人有一个终点,考虑相遇,那么几个相遇在一起的人他们的最终位置不过是他们内部互换罢了。怎样判断相遇呢?相遇即此时坐标相同,那么对于两个不同类型的人i,j,就满足这样的等式(设i从y轴出发,j从x轴出发):pi-ti=pj-tj(或者写成xi-ti=yj-tj),在这里可以理解为由于时间延迟,我们先让人们后退t步,那么就可以同时出发了。
接下来我们可以通过排序轻松地将人们按照(pi-ti)分成很多组,那么只有(pi-ti)相等(即同一组)的人们之间的位置是在内部互换的。问题进一步转化为在每一组内找到每个人对应的位置。
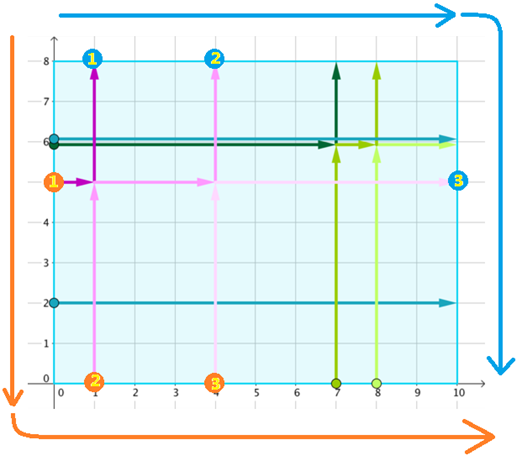
根据题目要求的转向关系,我们可以发现这样一个规律:
首先橙色的1,2,3号人是一组,他们可以相遇。我们发现如果将他们原先不考虑相遇的情况下的终点按照蓝色箭头从前到后排序,将橙色点按照橙色箭头从前到后排序,那么起点终点就正确对应了!也就轻松找到每个人的最终位置了!
最终这道题变成了重在书写排序关键字的题了……
1 #include<stdio.h> 2 #include<algorithm> 3 #define go(i,a,b) for(int i=a;i<=b;i++) 4 struct info{int Type,tot,x,y,id;};info a[100003],tmp[100003]; 5 bool cmp1(info A,info B){return A.tot==B.tot?(A.Type==B.Type? 6 (A.Type==2?(A.y>B.y):(A.x<B.x)):(A.Type<B.Type)):(A.tot<B.tot);} 7 bool cmp2(info A,info B){return A.Type==B.Type?(A.Type==2? 8 (A.y>B.y):(A.x<B.x)):(A.Type>B.Type);} 9 bool cmp3(info A,info B){return A.id<B.id;}int n,w,h,t; 10 int main() 11 { 12 scanf("%d%d%d",&n,&w,&h); 13 go(i,1,n) 14 { 15 int Type,p,t;scanf("%d%d%d",&Type,&p,&t); 16 if(Type==1)a[i]=(info){Type,p-t,p,h,i}; 17 if(Type==2)a[i]=(info){Type,p-t,w,p,i}; 18 } 19 std::sort(a+1,a+n+1,cmp1);int l=1,r=1; 20 while(l<=n) 21 { 22 while(a[l].tot==a[r+1].tot&&r+1<=n)r++; 23 t=0;go(i,l,r)tmp[++t]=a[i];std::sort(tmp+1,tmp+t+1,cmp2); 24 go(i,l,r)a[i].id=tmp[i-l+1].id;l=r=r+1; 25 } 26 std::sort(a+1,a+n+1,cmp3);go(i,1,n)printf("%d %d ",a[i].x,a[i].y);return 0; 27 }//Paul_Guderian
E. Goodbye Souvenir
调试了几乎一下午和一晚上……
·述大意:
输入n,m(1≤n,m ≤100 000)表示一个长度为n序列和m个操作,接下来输入这个序列。然后输入m个操作,操作分为两种:
Input:1 p x (1 ≤ p ≤ n, 1 ≤ x ≤ n), 将p位置的值(颜色)修改为x;
Input:2 l r(1≤l≤r≤n),询问区间[l,r]中所有出现至少两次的数的第一次出现的位置和最后一次出现的位置的距离和.
·分析:
我们发现修改+询问很难想。先试着去掉修改,只询问,那么应该怎么做呢?第一种方法一定是对于每种颜色维护区间最早位置和最晚位置,询问的时候相减就是答案了。另一种解法是为将来处理修改操作而考虑的——由于修改仅仅每次修改一个值,那么这一个值可能会影响答案,也可能不会,所以既然修改一个点,那么我们可以将答案这样统计:
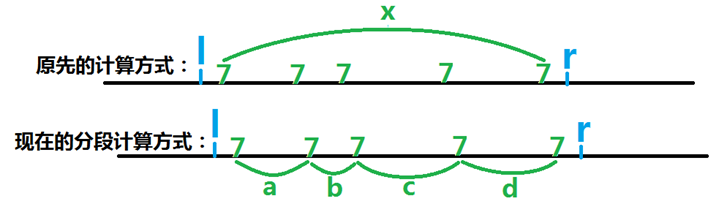
新的计算方式可以表示成如下式子:
设pre[x]表示向左和x位置上颜色(数字)相同最近位置。
那么结果就是: RES=∑(i-pre[i]+1) (i,pre[i]均在[l,r]内)
如果我们将所有颜色所有这样的二元组(pre[i],i)存起来,由于选择这个二元组就是一段长度,所以我们给这个二元组加上权值:i-pre[i]。那么每次询问区间内和的时候(记住pre[i]<i),其实就是询问满足pre[i]>=l且i<=r的二元组的权值和。这两个关键字的维护,看上去是一个前缀一个后缀,那么可以很容易想到用二维树状数组维护。然后MLE。为什么会这样?因为这道题在线算法似乎是不可能的,我们需要借助离线后询问之间的关系来简化。
离线询问。根据"pre[i]>=l且i<=r"的查找要求,那么先进行询问右端点排序,当到达r时,1~r的信息已经存入一维树状数组(很明显此时一维树状数组维护的是>=l的pre[i],在外面扫的指针维护的是i<=r),也就是说在r之前插入的二元组均满足条件'i<=r',然后我们在树状数组里面找出所有pre[i]>l的pre[i]的权值和就可以了。我们快乐地达到了降空间降时间的目的。此时为nlogn的级别。(上述方法不失为一种常用而高效的处理方式)
插播一句,用树状数组处理后缀信息和不仅可以做差也可反着插入元素从而转化为求前缀和。(比如Add(x,1)改为Add(n-x+1,1))
上述内容清晰之后,开始应对修改。带修带修,此处至少已经很清晰了,一种是使用嵌套的可持久化数据结构(此题可用主席树带树状数组),另一种是使用分治算法。很明显,CF将这个题归为data structures,出题人也仅仅给出了树套树的解法(网上有blog声称此法容易或已经MLE)。
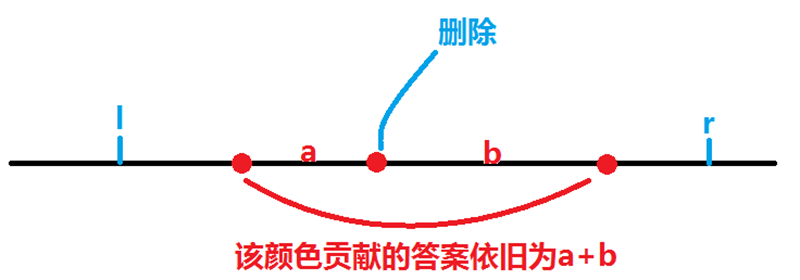
无论是从空间复杂度复杂度还是编码复杂度,CDQ分治在相比之下更加优秀。本题CDQ分治是来专门处理修改这一操作的——根据其常用思想,一个修改颜色操作视作删除当前颜色的点和添加新颜色的点两步,同时,由于我们上文提到,可能修改一个颜色,并不会产生影响,这种情况发生的条件是这个点小消失后左右两端的相同颜色点都在询问区间里,所以并不影响(见下图)。
据此对于每个修改操作实质上要分为5个操作:
pre[i],next[i]分别表示相同颜色前驱后继的位置。
对于旧颜色:
①减去(pre[i],i)②减去(i,next[i])③加上(pre[i],next[i])
对于修改后的颜色:
④加上(pre[i],i)⑤加上(i,next[i])
另外读入初始化的二元组也将作为添加操作加入CDQ分治的询问数组。
最后呢上述CDQ操作是以预处理完成的,详见下。
Let's try to give a summarize the solution.
在读入之后对于每种颜色维护一个set(替代平衡树)来查找前驱后继,离线所有操作,对于修改操作直接在set中修改然后记录前驱后继来存储分成的5个操作。完事后进行CDQ分治,CDQ分治以所有操作(包含修改和询问)的r为关键字(代码中的p),分治内部维护一维树状数组并以l为关键字(代码中的x),此处和上文没有修改操作时候的过程完全一样。
总结来说,没修改,就离线询问+树状数组;有修改,添上一个CDQ即可。
1 #include<set> 2 #include<cstdio> 3 #include<algorithm> 4 #define ll long long 5 #define go(i,a,b) for(int i=a;i<=b;i++) 6 using namespace std; 7 const int N=100010; 8 int k,n,m,q,color[N],x,y; 9 ll ans[N],c[N];bool yes[N]; 10 set<int>S[N];set<int>::iterator it; 11 struct info{int p,x,w,id;}Q[N*20],T[N*20]; 12 void Add(int x,int d){while(x<=n)c[x]+=d,x+=x&-x;} 13 ll Sum(int x){ll R=0;while(x)R+=c[x],x-=x&-x;return R;} 14 15 void Revise(int x,int y) 16 { 17 if(color[x]==y)return;it=S[color[x]].find(x);int left=0; 18 19 if(it!=S[color[x]].begin()){it--;left=(*it);it++; 20 Q[++m]=(info){x,left,-(x-left),0};}it++; 21 if(it!=S[color[x]].end()){Q[++m]=(info){*it,x,-((*it)-x),0}; 22 if(left)Q[++m]=(info){*it,left,(*it)-left,0};} 23 24 S[color[x]].erase(x);color[x]=y; 25 S[y].insert(x);it=S[y].find(x);left=0; 26 27 if(it!=S[y].begin()){it--;left=(*it);it++; 28 Q[++m]=(info){x,left,x-left,0};}it++; 29 if(it!=S[y].end()){if(left)Q[++m]=(info){*it,left,left-(*it),0}; 30 Q[++m]=(info){*it,x,(*it)-x,0};} 31 } 32 33 void CDQ(int l,int r) 34 { 35 if(l==r)return;int M=l+r>>1;CDQ(l,M);CDQ(M+1,r); 36 int p1=l-1,p2=M,t=l-1;go(i,l,r)T[i]=Q[i]; 37 38 while(p1<M||p2<r)if(p2>=r||(p1<M&&T[p1+1].p<=T[p2+1].p)) 39 Q[++t]=T[++p1],!Q[t].id?Add(n-Q[t].x+1,Q[t].w),1:1; 40 else Q[++t]=T[++p2],Q[t].id?ans[Q[t].id]+=Sum(n-Q[t].x+1),1:1; 41 42 go(i,l,p1)if(!T[i].id)Add(n-T[i].x+1,-T[i].w); 43 } 44 int main() 45 { 46 scanf("%d%d",&n,&q); 47 go(i,1,n)scanf("%d",&color[i]),S[color[i]].insert(i); 48 go(i,1,n){it=S[color[i]].find(i);if(it!=S[color[i]].begin())it--, 49 Q[++m]=(info){i,*it,i-(*it),0};} 50 go(i,1,q)scanf("%d%d%d",&k,&x,&y), 51 k==1?Revise(x,y),1:(Q[++m]=(info){y,x,0,i},yes[i]=1); 52 CDQ(1,m);go(i,1,q)if(yes[i])printf("%I64d ",ans[i]);return 0; 53 }
青春那么美生活却那么动荡,我梦想成为迪伦那样的歌手,
学着写歌唱出所有心底的想法。——————————汪峰《那年我五岁》