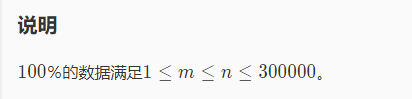1 // luogu-judger-enable-o2
2 #include<bits/stdc++.h>
3 #define ld double
4 using namespace std;
5 const int N=1<<20;
6 const ld pi=acos(-1);
7 int m,n,len,L,t1[N],t2[N],tot,ans[N],rev[N];
8 char s[N];
9 struct C{
10 ld x,y;
11 C(ld _x=0,ld _y=0):x(_x),y(_y){};
12 C operator +(const C&A)const{return C(x+A.x,y+A.y);}
13 C operator -(const C&A)const{return C(x-A.x,y-A.y);}
14 C operator *(const C&A)const{return C(x*A.x-y*A.y,x*A.y+y*A.x);}
15 C operator /(const ld&A)const{return C(x/A,y/A);}
16 }a[N],b[N],c[N];
17 void fft(C*a,int f){
18 for(int i=0;i<len;++i)if(i<rev[i])swap(a[i],a[rev[i]]);
19 for(int i=1;i<len;i<<=1){
20 C wn=C(cos(pi/i),f*sin(pi/i));
21 for(int j=0;j<len;j+=i<<1){
22 C w=C(1,0);
23 for(int k=0;k<i;++k,w=w*wn){
24 C x=a[j+k],y=w*a[i+j+k];
25 a[j+k]=x+y,a[i+j+k]=x-y;
26 }
27 }
28 }
29 if(!~f)for(int i=0;i<len;++i)a[i]=a[i]/len;
30 }
31 int main(){
32 // freopen("P4173.in","r",stdin);
33 // freopen("P4173.out","w",stdout);
34 scanf("%d%d",&m,&n);
35 scanf("%s",s);
36 for(int i=0;i<m;++i)t1[i]=s[m-i-1]=='*'?0:s[m-i-1]-'a'+1;
37 scanf("%s",s);
38 for(int i=0;i<n;++i)t2[i]=s[i]=='*'?0:s[i]-'a'+1;
39 for(len=1;len<n+m;len<<=1,L++);
40 for(int i=1;i<len;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
41
42 for(int i=0;i<len;++i)a[i].x=t1[i]*t1[i]*t1[i],a[i].y=0;
43 for(int i=0;i<len;++i)b[i].x=t2[i],b[i].y=0;
44 fft(a,1);fft(b,1);
45 for(int i=0;i<len;++i)c[i]=c[i]+a[i]*b[i];
46
47 for(int i=0;i<len;++i)a[i].x=t1[i]*t1[i],a[i].y=0;
48 for(int i=0;i<len;++i)b[i].x=t2[i]*t2[i],b[i].y=0;
49 fft(a,1);fft(b,1);
50 for(int i=0;i<len;++i)c[i]=c[i]-a[i]*b[i]*2;
51
52 for(int i=0;i<len;++i)a[i].x=t1[i],a[i].y=0;
53 for(int i=0;i<len;++i)b[i].x=t2[i]*t2[i]*t2[i],b[i].y=0;
54 fft(a,1);fft(b,1);
55 for(int i=0;i<len;++i)c[i]=c[i]+a[i]*b[i];
56
57 fft(c,-1);
58 for(int i=0;i<=n-m;++i){
59 int d=floor(c[i+m-1].x+0.5);
60 if(!d)ans[++tot]=i;
61 }
62 printf("%d
",tot);
63 for(int i=1;i<=tot;++i)printf("%d ",ans[i]+1);
64 return 0;
65 }