1 #include<bits/stdc++.h>
2 #define rg register
3 using namespace std;
4 const int M=320,N=200010;
5 int T,n,m,typ,sz,ch[N][26],Fl[N][26],fl[N],end[M][N],pos[M][N];
6 int sum[M][N],u,tot,bl[N],st[N],ed[N],lst,vis[N],len[N],s[N];
7 inline char gc(){
8 static char*p1,*p2,buf[1000000];
9 if(p1==p2)p2=(p1=buf)+fread(buf,1,1000000,stdin);
10 return(p1==p2)?EOF:*p1++;
11 }
12 inline int rd(){
13 int x=0;char c=gc();
14 while(c<'0'||c>'9')c=gc();
15 while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=gc();
16 return x;
17 }
18 void extend1(int l,int i){
19 int x=lst;
20 if(i-len[x]-1<l||s[i-len[x]-1]!=s[i])x=Fl[x][s[i]];
21 if(!ch[x][s[i]]){
22 len[++sz]=len[x]+2;
23 int y=fl[x];
24 if(s[i-len[y]-1]!=s[i])y=Fl[y][s[i]];y=ch[y][s[i]];
25 memcpy(Fl[sz],Fl[y],sizeof(Fl[y]));
26 Fl[sz][s[i-len[y]]]=fl[sz]=y;
27 ch[x][s[i]]=sz;
28 }
29 lst=x=ch[x][s[i]];
30 }
31 void extend2(int i,int r){
32 int x=lst;
33 if(i+len[x]+1>r||s[i+len[x]+1]!=s[i])x=Fl[x][s[i]];
34 if(!ch[x][s[i]]){
35 len[++sz]=len[x]+2;
36 int y=fl[x];
37 if(s[i+len[y]+1]!=s[i])y=Fl[y][s[i]];y=ch[y][s[i]];
38 memcpy(Fl[sz],Fl[y],sizeof(Fl[y]));
39 Fl[sz][s[i+len[y]]]=fl[sz]=y;
40 ch[x][s[i]]=sz;
41 }
42 lst=x=ch[x][s[i]];
43 }
44 int main(){
45 #ifndef ONLINE_JUDGE
46 freopen("loj6070.in","r",stdin);
47 freopen("loj6070.out","w",stdout);
48 #endif
49 typ=rd();n=rd();m=rd();
50 u = sqrt(n);
51 char c=gc();while(!isalpha(c))c=gc();
52 for(int i=1;i<=n;++i,c=gc()){
53 bl[i]=(i-1)/u+1;ed[bl[i]]=i;
54 if(!st[bl[i]])st[bl[i]]=i;
55 s[i]=c-'a';
56 }tot=bl[n];
57 sz=1;
58 fl[0]=1;fl[1]=0;
59 len[0]=0;len[1]=-1;
60 for(rg int i=0;i<26;++i)Fl[0][i]=1;
61 memset(end,0x3f,sizeof(end));
62 for(rg int i=1;i<=tot;++i){
63 lst=0;T++;
64 for(rg int j=st[i];j<=n;++j){
65 extend1(st[i],j);
66 sum[i][j]=sum[i][j-1];
67 if(vis[lst]<T){
68 vis[lst]=T;
69 sum[i][j]++;
70 end[i][lst]=j;
71 }
72 if(len[lst]==j-st[i]+1)pos[i][j]=lst;
73 else pos[i][j]=pos[i][j-1];
74 }
75 }
76 int ans=0;
77 for(rg int i=1,l,r;i<=m;++i){
78 T++;
79 l=rd();r=rd();
80 if(typ)l^=ans,r^=ans;
81 if(bl[l]==bl[r]){
82 lst=0;ans=0;
83 for(rg int j=l;j<=r;++j){
84 extend1(l,j);
85 if(vis[lst]<T)vis[lst]=T,ans++;
86 }
87 }else{
88 ans=sum[bl[l]+1][r];
89 lst=pos[bl[l]+1][r];
90 for(rg int j=ed[bl[l]];j>=l;--j){
91 extend2(j,r);
92 if(vis[lst]<T&&end[bl[l]+1][lst]>r)vis[lst]=T,ans++;
93 }
94 }
95 printf("%d
",ans);
96 }
97 return 0;
98 }
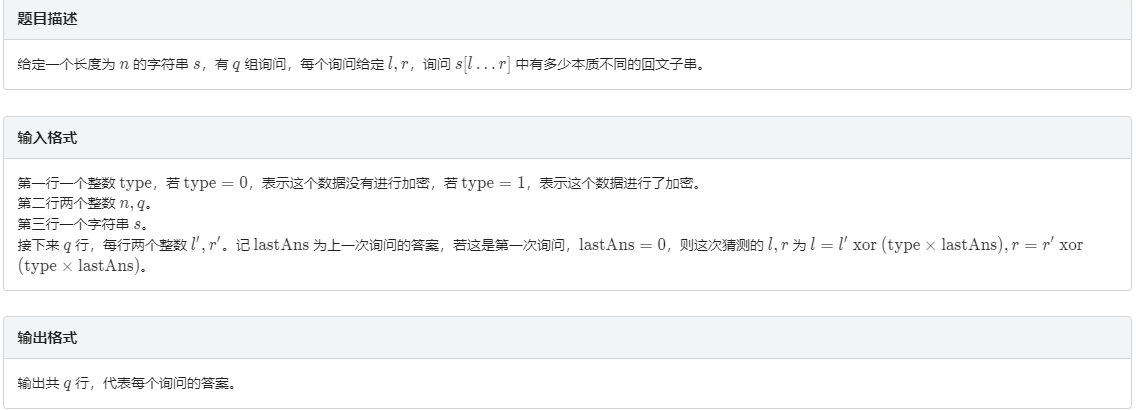
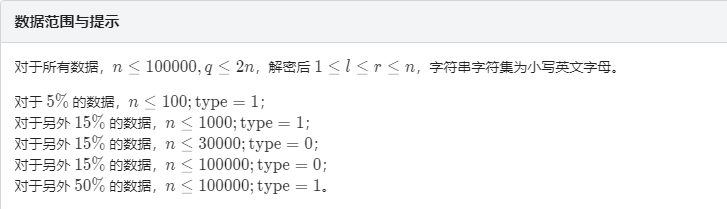
 题解:
题解: loj6070
loj6070