描述
在 Warcraft III 之冰封王座中,毁灭者是不死族打三本后期时的一个魔法飞行单位。
毁灭者的核心技能之一,叫做魔法吸收(Absorb Mana):
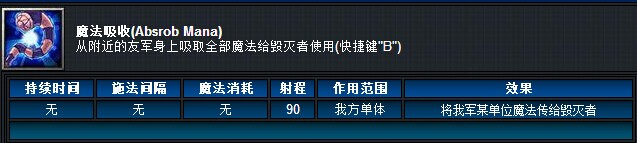
现在让我们来考虑下面的问题:
假设你拥有 n 个魔法单位,他们从左到有站在一行,编号从 1 到 n。 每个单位拥有三项属性:
-
si: 初始法力。
-
mi: 最大法力上限。
-
ri: 每秒中法力回复速度。
现在你操纵一个毁灭者,有 m 个操作,t l r,表示时刻 t,毁灭者对所有编号从 l 到 r 的单位,使用了魔法吸收。操作按照时间顺序给出,计算毁灭者一共吸收了多少法力。
输入
输入数据的第一行有一个整数 n (1 ≤ n ≤105) — 你的魔法单位的数目。
接下来的 n 行,每行有三个整数 si, mi, ri (0 ≤ si ≤ mi ≤ 105, 0 ≤ ri ≤ 105) 描述一个魔法单位。
接下来一行又一个整数 m (1 ≤ m ≤ 105), — 操作的数目。
接下来的 m 行,每行描述一个操作 t, l, r(0 ≤ t ≤ 109, 1 ≤ l ≤ r ≤ n),t 非降。
输出
输出一行一个整数表示毁灭者一共吸收了多少法力。
- 样例输入
-
5 0 10 1 0 12 1 0 20 1 0 12 1 0 10 1 2 5 1 5 19 1 5
- 样例输出
-
83
Solution:
如果魔法单位没有法力上限,这道题就是一道水题了,线段树即可搞定。
设置了法力上限,从维护区间的角度来考虑就比较困难了。
我们换一种思路,考虑对每一个魔法单位维护其遭遇收割的各个时刻,或者说其遭遇收割的时间序列(以下简称“时间序列”)。
这样就可以轻松求出毁灭者在各个魔法单位收割的法力值,做法如下:
为简单计,先假设所有魔法单位的初始法力都为零。
设魔法单位 $i$ 法力回满所需时间为 $T$,显然 $T=lceil frac{m_i}{r_i} ceil$ 。
考察相邻收割时刻 $t_k$与$t_{k+1}$,其间隔记做 $Delta t=t_{k+1}-t_{k}$,若 $Delta t<T$ 则$t_{k+1}$ 时刻收割的法力值为 $Delta t imes r_i$,否则为 $m_{i}$ 。
对于每个魔法单位我们只要知道其遭遇收割的时间间隔(以下简称“时间间隔”)中,大于等于$T$的时间间隔的个数以及小于 $T$ 的时间间隔的总和。
对每个魔法单位,我们可以用 map 来维护其遭受收割的时间序列,用树状数组来维护时间间隔之和与时间间隔的数量之和。
对每个魔法单位都按上述方式做一遍,时间上不能承受。同时应当注意到相邻魔法单位的时间序列是有联系的,可以动态维护
假设现在已经维护好了第 $i$ 个魔法单位的时间序列和时间间隔,在此基础上去掉所有以 $i$ 为区间右端点的收割时刻,再插入所有以 $i+1$ 为区间左端点的收割时刻,就得到了第 $i+1$ 个魔法单位的时间序列。
删除一个时刻 $t_{i}$ 意味着删除了两个时间间隔 $t_{i}-t_{i-1}$ 和 $t_{i+1}-t_{i}$,新增了一个时间间隔 $t_{i+1}-t_{i-1}$;插入一个时刻 $t_{i}$ 的作用恰好相反。
Implementation:
对每个魔法单位,先维护出以其为左端点和右端点的收割操作。然后从左到右动态维护各个魔法单位的时间序列,同时记录下相应的时间间隔的插入与删除操作。
对涉及到的所有时间间隔进行离散化。然后对每个魔法单位,先将其对应的(或称“贡献的”)时间间隔的插入与删除操作更新到树状数组中。
最后查询两类时间间隔贡献的法力加到答案中。
另外还要考虑到初始法力值可能不为零,这并不会带来什么困难,只要算一下毁灭者在每个魔法单位第一次吸收的法力的实际值和假设初始法力为零的情况之差,加到答案里去。
复杂度 $O((m+n)log m)$
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N(1e5+5); 5 typedef long long LL; 6 7 LL bit[N<<2]; 8 int a[N], m[N], r[N], bit2[N<<2]; 9 vector<int> Lt[N], Rt[N], op[N], b; 10 map<int,int> s; 11 12 void add(int x, int v, int n){ 13 for(; x<=n; bit[x]+=v, x+=x&-x); 14 } 15 16 LL sum(int x){ 17 LL res=0; 18 for(; x; res+=bit[x], x-=x&-x); 19 return res; 20 } 21 22 void Add(int x, int v, int n){ 23 for(; x<=n; bit2[x]+=v, x+=x&-x); 24 } 25 26 int Sum(int x){ 27 int res=0; 28 for(; x; res+=bit2[x], x-=x&-x); 29 return res; 30 } 31 32 int main(){ 33 int n, q; 34 scanf("%d", &n); 35 for(int i=1; i<=n; i++) scanf("%d%d%d", a+i, m+i, r+i); 36 scanf("%d", &q); 37 for(int l, r, t; q--; ){ 38 cin>>t>>l>>r; 39 Lt[l].push_back(t); 40 Rt[r].push_back(t); 41 } 42 s[0]++; 43 LL ans=0; 44 for(int i=1; i<=n; i++){ 45 for(auto &t: Rt[i-1]){ 46 if(--s[t]) continue; 47 auto p=s.lower_bound(t); 48 int pre, suc; 49 pre=(--p)->first, ++p, op[i].push_back(pre-t); 50 if(++p!=s.end()) 51 suc=p->first, op[i].push_back(t-suc), op[i].push_back(suc-pre), b.push_back(suc-pre); 52 s.erase(--p); //error-prone 53 } 54 for(auto &t: Lt[i]){ 55 if(s[t]++) continue; 56 auto p=s.lower_bound(t); 57 int pre, suc; 58 pre=(--p)->first, ++p, op[i].push_back(t-pre), b.push_back(t-pre); 59 if(++p!=s.end()) suc=p->first, op[i].push_back(suc-t), b.push_back(suc-t), op[i].push_back(pre-suc); 60 } 61 if(s[0]>1) ans+=a[i]; 62 else{ 63 auto p=s.begin(); 64 if(++p!=s.end()){ 65 int t=p->first; 66 ans+=min(a[i]+(LL)t*r[i], (LL)m[i])-min((LL)t*r[i], (LL)m[i]); //error-prone 67 } 68 } 69 } 70 sort(b.begin(), b.end()); 71 auto e=unique(b.begin(), b.end()); 72 int size=e-b.begin(); 73 for(int i=1; i<=n; i++){ 74 for(int &x: op[i]){ 75 int id=upper_bound(b.begin(), e, abs(x))-b.begin(); //error-prone 76 add(id, x, size); 77 if(x<0) Add(id, -1, size); 78 else Add(id, 1, size); 79 } 80 if(m[i]==0 || r[i]==0) continue; //error-prone 81 int t=(m[i]-1)/r[i]+1; 82 int id=lower_bound(b.begin(), e, t)-b.begin(); 83 ans+=(LL)(Sum(size)-Sum(id))*m[i]; 84 ans+=sum(id)*r[i]; 85 } 86 printf("%lld ", ans); 87 return 0; 88 }
代码中坑主要有
(1)注意需要用long long的地方
(2)别忘了将时刻从map中删除(代码第52行)
s.erase(--p); //error-prone
对拍才发现跪在这里的,多么痛的领悟。。。静态查错很重要啊。。。。。。。。。。。