Observations
含有 $n$ 个点且 key(以下也称 key 为「权值」)是 1 到 $n$ 的 BST 具有下列性质:
若 $k$ 是一个非根叶子且是个左儿子,则 $k$ 的父亲是 $k+1$ 。
证明:假设 $k$ 的父亲是 $p$ 且 $p
e k + 1$,则 $p > k + 1$;显然 $k + 1$ 不可能是 $k$ 的祖先。
设 $k$ 和 $k + 1$ 的最近公共祖先是 $t$,则有 $k < t < k + 1$ 或者 $ k + 1 < t < k$,矛盾!
同理可证,若 $k$ 是一个非根的叶子且是个右儿子,则 $k$ 的父亲是 $k - 1$ 。
注:上述性质也可以从「BST 的任意子树中 key 都是连续的」这个性质推出。
从而可以得出,striped BST 的所有叶子都是左儿子。
perfectly balanced BST 只有最后一层可能不满,其他层都是满的。
$n$ 个点的 perfectly balanced BST 的高度是 $floor{log n}$ 。
Q:是否只要满足
- 所有叶子节点都是左儿子
- 除了最后一层,每层都是满的
就一定存在一种填充权值的方案使得这棵树是一棵 perfectly balanced striped BST?
A:不是。
递推
有根树具有天然的递归结构。
容易看出
- perfectly balanced striped BST 的任意子树也是 perfectly balanced striped BST。
- 可以把任意一棵 $k$ 个点的子树的权值范围变成 $1$ 到 $k$ 且保持其为 striped BST。换言之,我们只需要考虑权值从 1 开始的情形。这里用到了 BST 的任意子树中 key 值连续的性质。
欲求 $n$ 个点的 perfectly balanced striped BST 的数量,可以枚举根节点的权值。一棵子树内的权值必定是连续的,根节点的权值确定后,根的左右子树的节点数就确定了。设根节点的权值是 $r$,则左子树中有 $r - 1$ 个点,权值范围是 $1$ 到 $r - 1$;右子树中有 $n - r$ 个点,权值范围是 $r + 1$ 到 $n$ 。左子树的根的权值的奇偶性须跟 $r$ 不同,换言之,左子树的根的权值须与其中点的个数的奇偶性相同。右子树的根节点的权值须跟 $r$ 同奇偶。设右子树的根的权值是 $w$;把右子树的权值平移到 $1$ 到 $n - r$ 以后,$w$ 对应于 $w - r$,$w$ 与 $r$ 同奇偶意味着 $w - r$ 是偶数。
总而言之,一个 $n$ 个节点,权值是 $1, 2, dots, n$ 的 perfectly balanced striped BST 能作为根的左子树的必要条件是其根的权值与其中节点数同奇偶;能作为根的右子树的必要条件是其根的权值是偶数。
设 $T_1, T_2$ 是两棵 perfectly balanced striped BST。
若以 $T_1$ 为左子树,$T_2$ 为右子树能组合成一棵新的 perfectly balanced striped BST,则 $T_1, T_2$ 除了需要满足上述条件外,还需满足二者高度相等或二者高度相差 $1$ 且高度较小者是完美二叉树。
注:从上一节的分析可知,子树是完美二叉树的情形,只有一个点的树这一种情况;即下图所示的情形
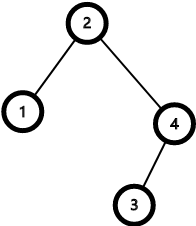
不难注意到,(i) 组合成的新树可以作为左子树当且仅当新树的右子树中有偶数个点;(ii) 组合成的新树可作为右子树当且仅当新树的左子树中有奇数个点。
对于 $n ge 5$,$n$ 个点的 perfectly balanced striped BST 的根节点的左右两棵子树的高度都不小于 1 。从上一节得出的两必要条件可以推出,此时左右两子树都不是完美二叉树,这意味着二者高度相同。设 $n$ 个点的 perfectly balanced BST 的高度是 $h$,则根的左右子树的高度都是 $h - 1$ 。
考虑高度为 $i$($i ge 2$)的 perfectly balanced striped BST,将其中能作为高度为 $i + 1$ 的 perfectly balanced striped BST 的根的左子树和右子树的 perfectly balanced striped BST 的「信息」分别放到两个列表 $L_i$ 和 $R_i$ 中。信息表为有序二元组:(节点数, 方案数)。
从 $L_i$ 中任取一元素 $ell$,从 $R_i$ 中任取一元素 $r$,通过组合 $ell, r$ 来构造 $L_{i + 1}$ 和 $R_{i + 1}$ 。
$L_{-1} = {(0, 1)}, R_{-1} = {(0, 1)}$;$(0, 1)$ 对应于空图
$L_0 = { (1, 1)}, R_0 = emptyset$;
$L_1 = {(2, 1)}, R_1 = {(2, 1)}$
$L_2 = {(4, 1), (5, 1)}, R_2 = {(4, 1)}$;$(4, 1)$ 是由 $L_0$ 中的 $(1,1)$ 和 $L_1$ 中的 $(2, 1)$ 组合得到的,上图即对应于 $(4, 1)$。
$L_3 = {(9, 1), (10, 1)}, R_3 = {(10, 1)}$
$L_4 = {(20, 1), (21, 1) }, R_4 = {(20, 1)}$
$vdots$
从以上分析中不难看出,给定 $n$,number of perfectly balanced striped binary search trees with $n$ vertices that have distinct integer keys between $1$ and $n$, inclusive 要么是 0 要么是 1。