<更新提示>
<正文>
T1 Gift
Description
人生赢家老王在网上认识了一个妹纸,然后妹纸的生日到了,为了表示自己的心 意,他决定送她礼物。可是她喜爱的东西特别多,然而他的钱数有限,因此他想 知道当他花一定钱数后剩余钱数无法再购买任何一件剩余物品(每种物品他最多 买一个)时有多少种方案,两种方案不同,当且仅当两种方案中至少有一件品不 同,可是由于他忙着准备泡下一个妹纸(chi),因此麻烦聪明的你帮帮忙。
Input Format
输入第一行 n 和 m, n 表示妹纸喜欢的礼物数目, m 表示现有的钱数,第二行 n 个数,表示 n 个物品的价格。
Output Format
输出一行一个数表示方案数目,答案对 1000000007 取模。
Sample Input
6 25
8 9 8 7 16 5
Sample Output
15
Hint
30%的数据: 0<=n<=100 0<=m<=500
100%的数据:0<=n<=1000 0<=m<=1000
注意:所有物品价格均小于 m
解析
如果存在一种合法的方案,就必然会有一个未购买并且价格最低的物品,并且这种方案的情况下,已经没有足够的钱来购买这个物品了。那么我们就以这个未购买的最小价格物品为基准点来统计答案,保证不重不漏。
我们先将所有物品按照价格从小到大排序,每次枚举一个物品(i),令这个物品作为上述未购买且价格最低的物品,然后,我们强制取第(1)到(i-1)个物品(如果不取,就和(i)个物品最小矛盾),并对第(i+1)到(n)个物品用(0/1)背包统计方案数,那么(sum_{jin [m-a[i]+1,m]}f[j])即为本次的答案。
我们发现每一次(dp)都是对后面连续的若干个物品进行计算,于是我们就可以放弃背包中滚动数组的做法,从(n)开始倒序(dp),并记录每一个阶段的(dp)值,然后在上述统计答案的过程中直接使用预处理的(dp)值即可。这样,时间复杂度就从(O(n^3))优化到了(O(n^2))。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N = 1020 , M = 1020;
const long long Mod = 1000000007;
int n,m,a[N];
long long f[N][M],ans,sum[N];
inline void input(void)
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
scanf("%d",&a[i]);
}
inline void dp(void)
{
memset( f , 0 , sizeof f );
f[n+1][0] = 1;
for (int i=n;i>=1;i--)
for (int j=0;j<=m;j++)
if ( j >= a[i] ) f[i][j] = ( f[i+1][j] + f[i+1][j-a[i]] ) % Mod;
else f[i][j] = f[i+1][j];
for (int k=1;k<=n;k++)
{
for (int i=m;i>=sum[k-1];i--)
f[k+1][i] = f[k+1][i-sum[k-1]];
for (int i=0;i<min(sum[k-1],1LL*m+1);i++)
f[k+1][i] = 0;
for (int i=m;i>=m-a[k]+1;i--)
ans = ( ans + f[k+1][i] ) % Mod;
}
}
int main(void)
{
input();
sort( a+1 , a+n+1 );
for (int i=1;i<=n;i++)
sum[i] = sum[i-1] + a[i];
dp();
if ( sum[n] > m ) printf("%lld
",ans%Mod);
else puts("1");
return 0;
}
T2 Fseq
Description
一个长度为 N+M 的数列,里面有 N 个+1,M 个-1 如果一个这样的数列被称作 F 序列(Fadeness) , 当且仅当它的任意前缀和均非 负。
for example :
1,-1,1,1,-1 is a Fadeness
1,-1,-1,1,1 is not because S(3) <0
求一个数列是 Fadensee 的概率。
Input Format
第一行, Test , 表示测试数据的组数。 每个数据 有两个数 N,M
Output Format
对于每组数据,输出一个实数(保留到小数点后 6 位)
Sample Input
3
1 0
0 1
1 1
Sample Output
1.000000
0.000000
0.500000
Hint
30%的数据: (Test<=10),(0<=N,M<=1000).
100%的数据: ( Test<=9008 ), ( 0<=N,M<=20000 ).
解析
和选举定理相似,我们直接转换成图形问题,然后应用反射原理即可。
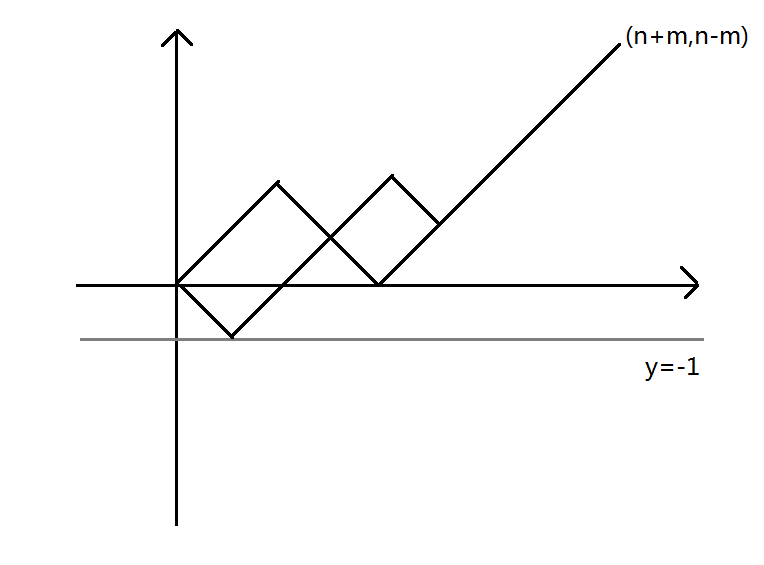
我们将数列取数形象地转化为坐标系中的移动问题,一开始在原点,每取一个(1)就向右上方走一步,横纵坐标各加(1),取一个(-1)就向右下方走一步,横坐标加(1),纵坐标减(1),那么最终折线会走到点((n+m,n-m))。
那么一旦折线接触到了直线(y=-1),这个序列就是不合法的。容易得出折线共有(C_{n+m}^m)种,那么问题在于求出不合法的折线数。
应用反射原理,由点((0,-2))为起点,向右上走(n+1)次,向右下走(m-1)次,最终到点((n+m,n-m))的所有折线就是不合法的折线数,我们同样可以得出这样的折线有(C_{n+m}^{m-1})种。
那么答案就是(frac{C_{n+m}^m-C_{n+m}^{m-1}}{C_{n+m}^m}),化简一下就是(1-frac{m}{n+1})。
(Code:)
#include<bits/stdc++.h>
using namespace std;
const int T = 10020 , N = 20020;
int t,n,m;
int main(void)
{
scanf("%d",&t);
while ( t-- )
{
scanf("%d%d",&n,&m);
if ( m > n ) puts("0.000000");
else printf("%.6lf
", 1.0 - 1.0 * m / (n+1) );
}
return 0;
}
<后记>