对于原网格图,将所有附加点顺次连接,并对这个封闭区域建立对偶图
为了避免误解,下面给出样例1的例子:
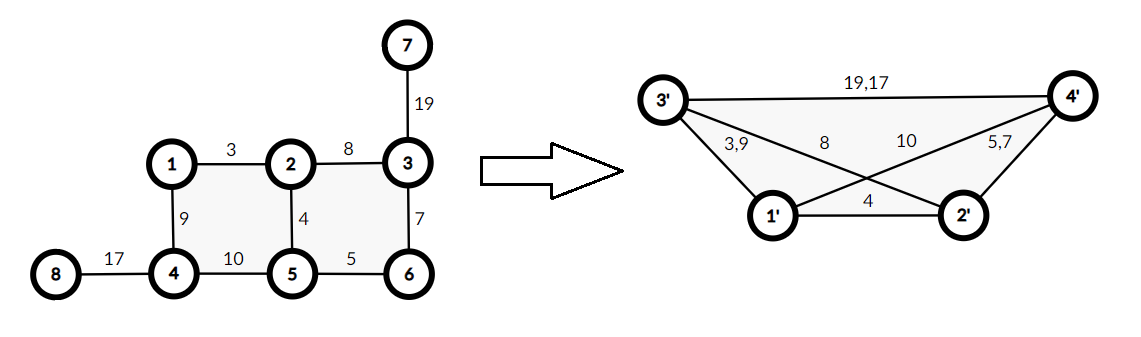
另外,称分割点指(对偶图中)在原网格图外的点,如例子中即为3'和4'
从原图的角度,问题即将所有点黑白染色(附加点颜色给定),并最小化两种颜色间的边权和
考虑染色后,仅保留其中的白点(以及之间的边)得到若干连通块,两种颜色之间的边即连通块向外部的边,且显然任意两个连通块与外部的边不会重复
进一步的,如果某个连通块不包含附加点,不妨将其全部反色,即去掉了这个连通块
由此,不难发现一个连通块向外部的边在对偶图中,总对应于若干条分割点之间的简单路径
实际上,这些简单路径可以理解为将两个分割点在原图中断开,使得原来的环分为两部分,再将这两部分重新首尾相连组成环,要求最终每一个环内附加点的颜色均相同
另外,注意到这些简单路径无公共边(不重复)且是在平面图上,不难得到过程中两个分割点必然会属于同一个环,且操作顺序不影响结果
若某两条路径以有公共端点,不妨最后执行这两次操作,分类讨论后总可以将其中一条路径删除或将两条路径合并成一条路径,重复此过程即可使得其不存在此类情况
进一步的,每一次操作后,新环拼接的首尾颜色要求相同(之后不会再选),同时若切割点的相邻两个附加点颜色本来就相同显然无意义,即相邻两个附加点颜色必然不同
另一方面,对于相邻两个附加点颜色不同的分割点,总要有一条路径以其为端点
换言之,即将这样的分割点两两配对(显然总是偶数个),每一对任选两者之间的一条路径,最终要求路径间无公共边且"拼接的首尾颜色相同"
事实上,无公共边的条件总可以通过调整配对方式来去掉公共的部分,因此不妨忽略
预处理出分割点两两最短路,再将这些分割点依次摊在序列上,"拼接的首尾颜色相同"即限制配对的两点中间分割点数量为偶数(变化偶数次即相同),进而破环为链(倍长)后区间dp即可
时间复杂度为$o(knm\log nm+k^{3})$,可以通过

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 505 4 #define K 105 5 #define ll long long 6 struct Edge{ 7 int nex,to,len; 8 }edge[N*N*4]; 9 struct Data{ 10 int x,pos,c; 11 bool operator < (const Data &k)const{ 12 return pos<k.pos; 13 } 14 }a[K]; 15 priority_queue<pair<ll,int> >Q; 16 int n,m,q,V,E,k,nn,x,pos,c,id[N][N],x1[N][N],x2[N][N],Id[K],head[N*N],vis[N*N]; 17 ll ans,d[N*N],g[K][K],f[K][K]; 18 int read(){ 19 int x=0; 20 char c=getchar(); 21 while ((c<'0')||(c>'9'))c=getchar(); 22 while ((c>='0')&&(c<='9')){ 23 x=x*10+c-'0'; 24 c=getchar(); 25 } 26 return x; 27 } 28 void add(int x,int y,int z){ 29 edge[E]=Edge{head[x],y,z}; 30 head[x]=E++; 31 if (E&1)add(y,x,z); 32 } 33 void dij(int k){ 34 memset(d,0x3f,sizeof(d)); 35 memset(vis,0,sizeof(vis)); 36 d[k]=0,Q.push(make_pair(0,k)); 37 while (!Q.empty()){ 38 int k=Q.top().second; 39 Q.pop(); 40 if (vis[k])continue; 41 vis[k]=1; 42 for(int i=head[k];i!=-1;i=edge[i].nex) 43 if (d[edge[i].to]>d[k]+edge[i].len){ 44 d[edge[i].to]=d[k]+edge[i].len; 45 Q.push(make_pair(-d[edge[i].to],edge[i].to)); 46 } 47 } 48 } 49 int main(){ 50 freopen("traffic.in","r",stdin); 51 freopen("traffic.out","w",stdout); 52 n=read(),m=read(),q=read(),V=(n-1)*(m-1)+1; 53 for(int i=1;i<n;i++) 54 for(int j=1;j<=m;j++)x1[i][j]=read(); 55 for(int i=1;i<=n;i++) 56 for(int j=1;j<m;j++)x2[i][j]=read(); 57 for(int i=1;i<n;i++) 58 for(int j=1;j<m;j++)id[i][j]=(i-1)*(m-1)+j; 59 while (q--){ 60 k=read(),E=nn=0,ans=1e18; 61 memset(head,-1,sizeof(head)); 62 memset(f,0,sizeof(f)); 63 for(int i=0;i<k;i++)a[i].x=read(),a[i].pos=read(),a[i].c=read(); 64 sort(a,a+k); 65 for(int i=0;i<k;i++) 66 if (a[i].c!=a[(i+k-1)%k].c)Id[nn++]=i; 67 if (!nn){ 68 printf("0\n"); 69 continue; 70 } 71 for(int i=1;i<n;i++) 72 for(int j=2;j<m;j++)add(id[i][j-1],id[i][j],x1[i][j]); 73 for(int i=2;i<n;i++) 74 for(int j=1;j<m;j++)add(id[i-1][j],id[i][j],x2[i][j]); 75 for(int i=0;i<k;i++)add(V+i,V+(i+1)%k,a[i].x); 76 int p=0; 77 for(int i=1;i<m;i++){ 78 while ((p<k)&&(a[p].pos<=i))p++; 79 add(id[1][i],V+p%k,x2[1][i]); 80 } 81 for(int i=1;i<n;i++){ 82 while ((p<k)&&(a[p].pos<=m+i))p++; 83 add(id[i][m-1],V+p%k,x1[i][m]); 84 } 85 for(int i=m-1;i;i--){ 86 while ((p<k)&&(a[p].pos<=n+(m<<1)-i))p++; 87 add(id[n-1][i],V+p%k,x2[n][i]); 88 } 89 for(int i=n-1;i;i--){ 90 while ((p<k)&&(a[p].pos<=(n+m<<1)-i))p++; 91 add(id[i][1],V+p%k,x1[i][1]); 92 } 93 for(int i=0;i<nn;i++){ 94 dij(V+Id[i]); 95 for(int j=0;j<nn;j++)g[i][j]=d[V+Id[j]]; 96 } 97 for(int i=(nn<<1)-1;i>=0;i--) 98 for(int j=i+1;j<(nn<<1);j+=2){ 99 f[i][j]=1e18; 100 for(int l=i+1;l<=j;l+=2)f[i][j]=min(f[i][j],g[i%nn][l%nn]+f[i+1][l-1]+f[l+1][j]); 101 } 102 for(int i=0;i<nn;i++)ans=min(ans,f[i][i+nn-1]); 103 printf("%lld\n",ans); 104 } 105 return 0; 106 }
