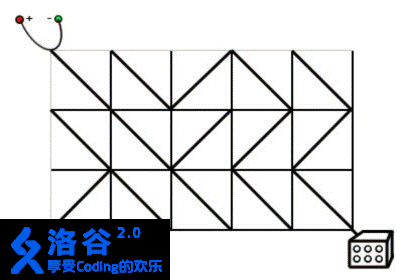
题意:如图一个(n*m(n,m<=500))的魔板,求从左上角到右下角最少需要翻转几根对角线?
分析:把魔板上的每个格点看作无向图中的一个节点,在对角线上的两个节点连边,如果魔板上本来就有这条对角线,则边权为0,否则边权为1.按照这样建图,则得到了一个边权为0或1的无向图.
通过双端队列从起点开始跑广搜.从u拓展到v的时候,如果这条边的权值为0,则点v从队头入队,否则从队尾入队.
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define ll long long
using namespace std;
inline int read(){
int x=0,o=1;char ch=getchar();
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')o=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*o;
}
const int M=2000005;
int n,m,dis[M];
char s[505][505];
int tot,head[M],nxt[M],to[M],w[M];
inline void add(int a,int b,int c){
nxt[++tot]=head[a];head[a]=tot;
to[tot]=b;w[tot]=c;
}
inline void bfs(){
for(int i=1;i<=(n+1)*(m+1);++i)dis[i]=1e9;//初始化
deque<int>q;q.clear();q.push_back(1);dis[1]=0;//初始化
while(q.size()){
int u=q.front();q.pop_front();
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(dis[v]>dis[u]+w[i]){
dis[v]=dis[u]+w[i];
if(v==(n+1)*(m+1)){
printf("%d
",dis[v]);
return;
}
if(!w[i])q.push_front(v);
else q.push_back(v);
}
}
}
}
int main(){
int T=read();
while(T--){
n=read(),m=read();
tot=0;for(int i=1;i<=(n+1)*(m+1);++i)head[i]=0;//多组数据初始化
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j){
cin>>s[i][j];
int a=(m+1)*(i-1)+j,b=(m+1)*i+j;
if(s[i][j]=='/'){
add(a,b+1,1);add(b+1,a,1);
add(a+1,b,0);add(b,a+1,0);
}
else{
add(a,b+1,0);add(b+1,a,0);
add(a+1,b,1);add(b,a+1,1);
}
}
if((n+m)&1){puts("NO SOLUTION");continue;}//特判无解
else bfs();
}
return 0;
}
