前言
这道题把U群搞得很热闹,顺便教育了一波自以为卡常的菜逼(我)。
题目
讲解
普通版
我们发现虽然总共有 3 种车可以选,但是每个地图有 1 种车不能选,所以排除掉离谱的 3-SAT 之后,还是一个比较简单的 2-SAT 板题。
一个比较 naive 的想法是枚举 x 处选什么车,这样复杂度是 \(O(3^dn)\) 的,应该在哪里都过不了,说不定能过原始数据。
但实际上我们只需要枚举 x 处选什么地图,根据鸽巢原理,我们发现任意两个地图就可以包含三种车,所以复杂度变成 \(O(2^dn)\),普通版可过。
炼狱版
WARNING:前方高能,非战斗人员请迅速撤离!
但是普通版的代码交到 UOJ 上是过不了的,我的代码会 T 在 extest12 上,而且我们一个机房都过不了。
于是我就去 U 群里面问
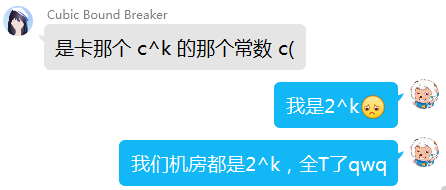
EI 表示是卡常(此时我以为正解就是c=2)
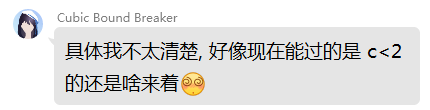
然后事情就不对劲起来了
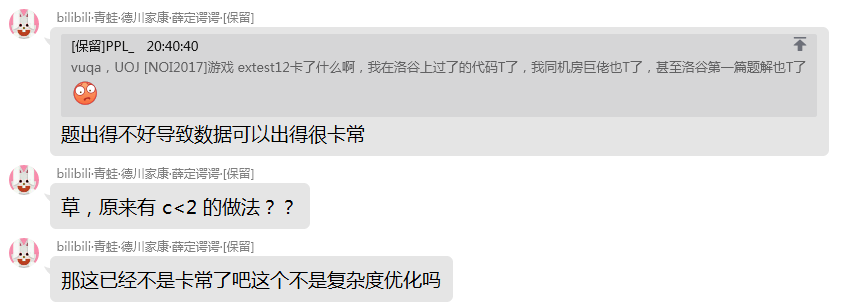
其中混进了一只萌萌的兔(蛙)队
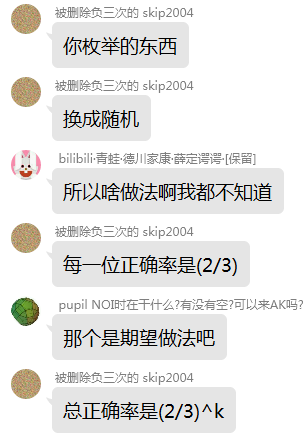
随后 $哥哥 给出做法
最后一个我不认识的大佬给出补充
大家都看懂了吧,那我就不讲了,所以复杂度就是 \(O(1.5^dn)\)。
代码
普通版
//12252024832524
#include <bits/stdc++.h>
#define TT template<typename T>
using namespace std;
typedef long long LL;
const int MAXN = 50005 << 1;
int n,m;
char c[MAXN];
LL Read()
{
LL x = 0,f = 1;char c = getchar();
while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9'){x = (x*10) + (c^48);c = getchar();}
return x * f;
}
TT void Put1(T x)
{
if(x > 9) Put1(x/10);
putchar(x%10^48);
}
TT void Put(T x,char c = -1)
{
if(x < 0) putchar('-'),x = -x;
Put1(x); if(c >= 0) putchar(c);
}
TT T Max(T x,T y){return x > y ? x : y;}
TT T Min(T x,T y){return x < y ? x : y;}
TT T Abs(T x){return x < 0 ? -x : x;}
char gc(){
char c = getchar();
while(c > 'D' || c < 'A') c = getchar();
return c;
}
vector<int> arb;
int head[MAXN],tot;
struct edge{
int v,nxt;
}e[MAXN<<1];
void Add_Edge(int u,int v){
e[++tot] = edge{v,head[u]};
head[u] = tot;
}
int cs[MAXN][2],E[MAXN][4];
void Get(int i,char s){
if(s == 'a') cs[i][0] = 1,cs[i][1] = 2;
else if(s == 'b') cs[i][0] = 0,cs[i][1] = 2;
else if(s == 'c') cs[i][0] = 0,cs[i][1] = 1;
}
int Find(int x,int s){
if(cs[x][0] == s) return 0;
else if(cs[x][1] == s) return 1;
return 2;
}
int dfn[MAXN],dfntot,bl[MAXN],qlt,low[MAXN],st[MAXN],tl;
bool ins[MAXN];
void Tarjan(int x){
ins[x] = 1; st[++tl] = x;
dfn[x] = low[x] = ++dfntot;
for(int i = head[x],v; i ;i = e[i].nxt){
v = e[i].v;
if(!dfn[v]) Tarjan(v),low[x] = Min(low[x],low[v]);
else if(ins[v]) low[x] = Min(low[x],dfn[v]);
}
if(dfn[x] == low[x]){
int v; bl[x] = ++qlt;
do{
bl[v = st[tl--]] = qlt;
ins[v] = 0;
}while(v ^ x);
}
}
void solve(){
for(int i = (n<<1);i >= 1;-- i) dfn[i] = head[i] = bl[i] = ins[i] = 0;
tl = qlt = tot = dfntot = 0;
for(int i = 1,A,B;i <= m;++ i){
if((A = Find(E[i][0],E[i][1])) > 1) continue;
B = Find(E[i][2],E[i][3]);
if(B > 1) Add_Edge(E[i][0]+n*A,E[i][0]+n*(A^1));//can't be chosen
else Add_Edge(E[i][0]+n*A,E[i][2]+n*B),Add_Edge(E[i][2]+n*(B^1),E[i][0]+n*(A^1));
}
for(int i = 1;i <= (n<<1);++ i) if(!dfn[i]) Tarjan(i);
for(int i = 1;i <= n;++ i) if(bl[i] == bl[i+n]) return;
for(int i = 1;i <= n;++ i) putchar('A'+cs[i][bl[i+n] < bl[i]]);
exit(0);
}
void dfs(int x){
if(x == arb.size()){
solve();
return;
}
for(char s = 'a';s < 'c';++ s) {
Get(arb[x],s);
dfs(x+1);
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = Read(); Read();
scanf("%s",c+1);
for(int i = 1;i <= n;++ i)
if(c[i] == 'x') arb.emplace_back(i);
else Get(i,c[i]);
m = Read();
for(int i = 1;i <= m;++ i) E[i][0] = Read(),E[i][1] = gc()-'A',E[i][2] = Read(),E[i][3] = gc()-'A';
dfs(0);
Put(-1,'\n');
return 0;
}
炼狱版?
//12252024832524
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define TT template<typename T>
using namespace std;
typedef long long LL;
const int MAXN = 50005 << 1;
int n,m,D;
char c[MAXN];
LL Read()
{
LL x = 0,f = 1;char c = getchar();
while(c > '9' || c < '0'){if(c == '-')f = -1;c = getchar();}
while(c >= '0' && c <= '9'){x = (x*10) + (c^48);c = getchar();}
return x * f;
}
TT void Put1(T x)
{
if(x > 9) Put1(x/10);
putchar(x%10^48);
}
TT void Put(T x,char c = -1)
{
if(x < 0) putchar('-'),x = -x;
Put1(x); if(c >= 0) putchar(c);
}
TT T Max(T x,T y){return x > y ? x : y;}
TT T Min(T x,T y){return x < y ? x : y;}
TT T Abs(T x){return x < 0 ? -x : x;}
mt19937 ee(time(0));
char gc(){
char c = getchar();
while(c > 'D' || c < 'A') c = getchar();
return c;
}
vector<int> arb;
int head[MAXN],tot;
struct edge{
int v,nxt;
}e[MAXN<<1];
void Add_Edge(int u,int v){
e[++tot] = edge{v,head[u]};
head[u] = tot;
}
int cs[MAXN][2],E[MAXN][4];
void Get(int i,char s){
if(s == 'a') cs[i][0] = 1,cs[i][1] = 2;
else if(s == 'b') cs[i][0] = 0,cs[i][1] = 2;
else if(s == 'c') cs[i][0] = 0,cs[i][1] = 1;
}
int Find(int x,int s){
if(cs[x][0] == s) return 0;
else if(cs[x][1] == s) return 1;
return 2;
}
int dfn[MAXN],dfntot,bl[MAXN],qlt,low[MAXN],st[MAXN],tl;
bool ins[MAXN];
void Tarjan(int x){
ins[x] = 1; st[++tl] = x;
dfn[x] = low[x] = ++dfntot;
for(int i = head[x],v; i ;i = e[i].nxt){
v = e[i].v;
if(!dfn[v]) Tarjan(v),low[x] = Min(low[x],low[v]);
else if(ins[v]) low[x] = Min(low[x],dfn[v]);
}
if(dfn[x] == low[x]){
int v; ++qlt;
do{
bl[v = st[tl--]] = qlt;
ins[v] = 0;
}while(v ^ x);
}
}
void solve(){
for(int i = (n<<1);i >= 1;-- i) dfn[i] = head[i] = bl[i] = ins[i] = 0;
tl = qlt = tot = dfntot = 0;
for(int i = 1,A,B;i <= m;++ i){
if((A = Find(E[i][0],E[i][1])) > 1) continue;
B = Find(E[i][2],E[i][3]);
if(B > 1) Add_Edge(E[i][0]+n*A,E[i][0]+n*(A^1));//can't be chosen
else Add_Edge(E[i][0]+n*A,E[i][2]+n*B),Add_Edge(E[i][2]+n*(B^1),E[i][0]+n*(A^1));
}
for(int i = 1;i <= (n<<1);++ i) if(!dfn[i]) Tarjan(i);
for(int i = 1;i <= n;++ i) if(bl[i] == bl[i+n]) return;
for(int i = 1;i <= n;++ i) putchar('A'+cs[i][bl[i+n] < bl[i]]);
exit(0);
}
char ff[10][3];
void dfs(int x){
if(clock() > 1.98*CLOCKS_PER_SEC){
Put(-1,'\n');
exit(0);
}
if(x == D){
solve();
return;
}
for(int s = 0;s < 2;++ s) {
Get(arb[x],ff[x][s]);
dfs(x+1);
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = Read(); D = Read();
scanf("%s",c+1);
for(int i = 1;i <= n;++ i)
if(c[i] == 'x') arb.emplace_back(i);
else Get(i,c[i]);
m = Read();
for(int i = 1;i <= m;++ i) E[i][0] = Read(),E[i][1] = gc()-'A',E[i][2] = Read(),E[i][3] = gc()-'A';
for(int i = 0;i < D;++ i){
ff[i][0] = 'a'; ff[i][1] = 'b'; ff[i][2] = 'c';
shuffle(ff[i],ff[i]+3,ee);
}
dfs(0);
Put(-1,'\n');
return 0;
}
后记
炼狱版代码加个?是因为那个不是炼狱版正解(我懒得写正解了),而是O2O3+随机地图+掐表的代码,虽然过了,但不保证每次都能过。
在我写完题解的时候(2022.3.4 21:42) U群仍未停止讨论,有大佬试图找出 \(O(1.5^dn)\) 的确定性做法,如果讨论出来了,我可能会更新。