前言
好吧,我承认,第一遍学网络流的时候就压根没学懂。甚至连板子都不会打
现在做题积累一些经验,自己理解最快的当然是自己写的东西,就从每道网络流的题里面总结咯~
本博客经过多次缝缝补补,如果哪里读着感觉前后突兀,很可能不是连续写的,劳请指出,我会尽快改。
网络流专题基本结束,很难再更新了qwq。
正题
记得前向星 tot 初值附 1 !!!
在限制对立的情况下,可以采用总边权-最小割求答案。
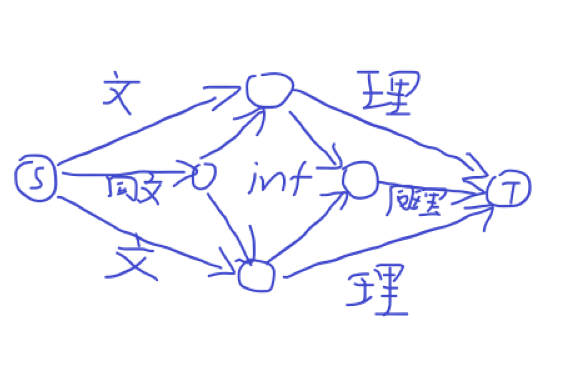
如此题可以 S --文边权--> 学生 --理边权--> T 。
在有额外奖励的时候,我们考虑怎么割从而建图。由于同文同理本质相同,故此处只讨论割同理的情况。
显然如果是割同理,意思就是说选了文就会割同理,于是我们需要将所有文连向同理以构成两者必割其一的态势(割同文与其类似):
这里我们利用的是两者无法共存,转化到图上就是存在路径从源点S经过两者到汇点T,造成两者必割其一的局面。
与上一题几乎一模一样,只不过两个同学换成了相邻的同学和自己而已。
这道题变成了两两不同时获得奖励,也就是说相同时需要割,但可以转化。
由于是个网格图,显然可以黑白染色,我们只需把其中一种颜色翻转即可,此时就变成了我们熟悉的两两不同时需要割。
还有这道题是和相邻的相同(转化后变为不同)需要割,有一个不同就割一个,不是一次性割完,但实际上是一样的,我们只需要把不同的当做两个点的点权和即可,而且这道题不需要建虚点,十分方便。
看了看题解,发现有最大权闭合子图的理解,但是个人认为有更好的理解方式(对于我自己来说)。
首先这道题与我们之前不同的是存在负贡献,由负贡献可以得到正贡献,这可怎么办呢?
其实还是考虑总正贡献-最小割,将花费和损失的代价转化为最小割,并利用内在的逻辑关系建图。
那么建图就很清晰了:S --花费--> 基站u,v --INF--> 用户c --利润--> T。
最大密度子图板题。
边除以点最大,可以联想到分数规划问题,也就是我们需要二分一个 (g),检查 (sum e - gsum v le 0)。
第一个思路是最大权闭合子图,考虑选了把边当成点,选了边必选它的两个点。
第二个思路是一个简单容斥,由于沐目女未写得浅显易懂而且相当短,我这里就不写了。 (^o^)/
洛谷题解是真的臭长。
已经可以自己建图了!
考虑一条边要么被入点删要么被出点删,就是一个二选一的问题,要求花费最小,很容易想到最小割。
直接左边 (n) 个点表示入点,与源点相连,边权为删的代价,右边 (n) 个点表示出点,与汇点相连,边权也为删的代价。
题中的边要删就代表左边的一个入点向右边的一个出点连正无穷的边,最小割就是答案。
输出方案也很简单,从源点在残留网络上沿着有流量的边跑,左边没经过的与右边经过的点是需要执行删除操作的,证明比较显然。
无源汇上下界可行流。
设一条边的流量下界为 (L_i),上界为 (R_i),假设每条边初始流量就是 (L_i),新图的容量为 (R_i-L_i)。
这样我们可以得到一些需要更多流出和更多流入的点,新建源点汇点,然后分流即可。
一定要注意我们假设时其实还没有流量!
-
如果流入的更多,表示我们需要强制流出更多,所以从源点新建一条边连向这个点,货到了,来取。
-
如果流出的更多,表示我们需要强制流入更多,所以从这个点新建一条边连向汇点,要出货,快给。
在新图上跑最大流,如果答案等于新建边权和(满流)则有解,反之无解,正确性显然。
这里的边权和显然是源点、汇点其中一边的边权和。
有源汇上下界可行流。
既然它都把源汇给出来了,直接在原图上跑不就行了?
然而源点和汇点不满足流量守恒!所以我们直接强制其守恒即可。
具体地,我们从汇点连一条容量无限的边到源点,然后跑无源汇上下界可行流即可。
然而这道题是有源汇上下界最小流,而且有大坑,先给图再讲。
*时刻记住网络流不能存在汇点向源点的连边!
首先题中给定的源汇点是 (1) 和 (n),跑最小流的思路是先跑可行流满足限制,然后减去倒着跑的最大流。
这道题的坑点是 (n) 可能向 (1) 连边,也就是说如果存在一条 (1) 到 (n) 且流量为 (5) 的边与一条 (n) 到 (1) 流量为 (3) 的边,答案应该是 (2),此时原图(第一层)不够用,原因是存在 (n) 向 (1) 的连边,我们需要建立第二层图。
建立 (s,t),连边如图所示,(t) 向 (s) 连边其实就是可行流中的操作,目的是让源汇点流量守恒、解决坑点、记录可行流答案,其实就是可以让流量反悔,实现最小流。
为了满足上下界的限制,我们还需要建立第三层图(第二层图的汇点还是有连源点的边),而第三层图中的红边其实就和无源汇上下界中的连边意义相同了,代表的是强制流量的连边。
我们在第三层图上跑一遍就可以得到一个满足上下界限制的残留网络,注意可行流是第二层图中反边的流量(因为它记录的才是原图的可行流,而不是我们跑出来的最大流)!
然后删去红边,在残留网络中的第二层图中反向跑出一个最大流,用前者减后者就是最小流,读者可以自行思考删红边以及在第二层图中反向跑最大流的意义。
建图代码
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = Read(); m = Read();
for(int i = 1;i <= m;++ i)
{
int u = Read(),v = Read(),c = Read(),opt = Read();
if(opt == 1) //must be fully filled
Add_Double_Edge(u,v,0),d[v] += c,d[u] -= c,L[i] = c;
else //otherwise
Add_Double_Edge(u,v,c);
}
Add_Double_Edge(n+2,1,INF); Add_Double_Edge(n,n+3,INF);//do not destroy!
for(int i = 1;i <= n;++ i)
if(d[i] > 0) Add_Double_Edge(0,i,d[i]),S += d[i];
else if(d[i] < 0) Add_Double_Edge(i,n+1,-d[i]);
Add_Double_Edge(n+3,n+2,INF); //re edge
if(dinic(0,n+1) == S)
{
int ff = e[tot].w;
clr(n+3); clr(n+2); //destroy these edges
for(int i = 1;i <= n;++ i)
if(d[i] > 0) clr(0),clr(i);
else if(d[i] < 0) clr(i),clr(n+1);
Put(ff-dinic(n+3,n+2),'
');
for(int i = 1;i <= m;++ i)
Put(e[(i<<1)^1].w+L[i],i == m ? '
' : ' ');
}
else printf("Impossible
");
return 0;
}
/*
1st : 1,n
2nd : n+2,n+3
3rd : 0,n+1
*/
顺便把有源汇上下界最大流也说了,拆边之后在残留网络正着跑,加上这个新贡献即可。
但是还没做到例题,锅了别找我。
找到例题了:P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流
由于这道题初始汇点没有连向源点的边,所以只需要两层图。
建图代码
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
while(~scanf("%d %d",&n,&m))
{
tot = 1;
for(int i = 0;i <= m+n+3;++ i) d[i] = head[i] = 0;
for(int i = 1,val;i <= m;++ i) val = Read(),d[0] -= val,d[i] += val,Add_Double_Edge(0,i,INF);
for(int i = 1;i <= n;++ i)
{
int C = Read(),D = Read();
Add_Double_Edge(m+i,m+n+1,D);
while(C --> 0)
{
int G = Read()+1,l = Read(),r = Read();
Add_Double_Edge(G,m+i,r-l);
d[G] -= l; d[m+i] += l;
}
}
int ss = 0;
for(int i = 0;i <= m+n+1;++ i)
if(d[i] > 0) Add_Double_Edge(m+n+2,i,d[i]),ss += d[i];
else if(d[i] < 0) Add_Double_Edge(i,m+n+3,-d[i]);
Add_Double_Edge(m+n+1,0,INF);
if(dinic(m+n+2,m+n+3) == ss)
{
int ans = e[tot].w;
clr(m+n+1); clr(0);
for(int i = 0;i <= m+n+1;++ i)
if(d[i] > 0) clr(m+n+2),clr(i);
else if(d[i] < 0) clr(i),clr(m+n+3);
Put(ans+dinic(0,m+n+1),'
');
}
else Put(-1,'
');
putchar('
');
}
return 0;
}
有源汇上下界可行流板题。
经典矩阵题Matrix Decompressing的加强版。
左边 (n) 个点表示行,右边 (m) 个点表示列。
S 向左边的点连边,右边的点向 T 连边,容量为行/列的和,中间 (n,m) 点互相连,流量表示矩阵对应位置的元素大小。
这道题给了一些元素大于小于等于的限制,相当于就是上下界可行流,由于没有从 T 到 S 的边,直接跑就行。
弱化版只要求每个元素在 ([1,20]) 之间,转化成 ([0,19]) 可以跑最大流(当然直接上下界也行)。
注意到绝对值在 (sum) 外面,所以还是可以行列整体考虑。
求最大值最小直接考虑二分,然后转有源汇上下界可行流即可。由于这道题的源汇点存在强制流量,所以要建反边而且还要再加一层图(你可以从上文理解“层”)。
最小费用最大流。
这种边的流量极小,费用不等就直接拆边,因为保证了拆的边费用高于之前的,所以一定合理。
不一定要求最大流怎么办?新建源点,向起点连需要的流量,费用为 (0) 即可。
无向图,找一条从 (1) 到 (n) 边不交的回路。
这题神了,首先因为是无向图,所以不用找来回,直接找两条路即可。
如何做到边不交?不用管,无向图该怎么连边就怎么连边!因为走一次之后边会被反向,再正向走不会有边,如果反向走就不会走最开始连的正费用的边,而会走反向的负费用的边,从而达到只走一次的效果。
找两条路?当然是新建源点,连起点一条流量为 (2),费用为 (0) 的边。
最小费用上下界可行流。
好吧其实这是我瞎编的名词,这玩意和普通上下界类似,也是利用了强制流量的思想,当然费用流的强制流量费用为 (0),只有题目给的边才会有费用。
依然是新建源汇点,然后连一条反向的极大边反悔。然后直接跑最小费用最大流。
想不起来了看看代码吧
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n = Read();
for(int i = 1;i <= n;++ i)
{
int k = Read();
for(int j = 1;j <= k;++ j)
{
int b = Read(),w = Read();
--d[i]; ++d[b]; S += w;
Add_Double_Edge(i,b,INF,w);
}
}
for(int i = 2;i <= n;++ i) Add_Double_Edge(i,n+1,INF,0);
for(int i = 1;i <= n;++ i)
if(d[i] > 0) Add_Double_Edge(0,i,d[i],0);
else if(d[i] < 0) Add_Double_Edge(i,n+2,-d[i],0);
Add_Double_Edge(n+1,1,INF,0);
MCMF(0,n+2);
Put(mc+S,'
');
return 0;
}
又是二选一,直接上最小割。
猜个结论:不能同时选的数可以做成二分图放在两边,然后就过了。
两个奇数的平方和一定不是完全平方数,两个偶数的gcd一定不为1。
然后就把所有的数分成奇数和偶数两个集合,然后再跑最小割就完事了。
最短路、最小割二合一融合怪,而且题目直接把做法写脸上了。
最短时间->最短路,然后要求让最短路增大,不就是把最短路割了吗?按最短路的边、割的费用建图,直接最小割,搞定。
最大权闭合子图。
原边流量改为 INF,S --点权--> 正权点,负权点 --点权(绝对值)--> T
正点权和减最小割为答案,割负点表示选,割正点表示不选,讨论一下正权点和负权点的依赖关系正确性即可得证。
这道题只需要把互相保护以及躲在这些之后后面的植物去掉,然后跑最大权闭合子图就行了。
混合图欧拉路。
- 欧拉回路
无向边先随便定向,然后根据入度出度向源汇点连边,有点像上下界里面的强制流量。
如果存在入度-出度是奇数的点无解,否则入度大的向汇点连流量为 (frac{|in-out|}{2}) 的边,出度大的从源点连边。
原图定向的无向边流量为 (1),相当于就是我告诉你那些点需要反向多少什么类型的边,有哪些边可以反向。
满流即有解,注意判断连通性。
- 欧拉通路
如果入度-出度是奇数的点个数大于 (2),无解,如果有两个,考虑在它们之间连一条无向边,转为欧拉回路问题。