前言
几乎送我退役的一道题
仔细想想其实不难 水一篇博客吧
题目
样例输入
样例输入1
5
2 1 1 0
1 3 0 1
2 4 1 2
5 2 1 1
样例输出1
1 2
样例解释1
操作路径 {2, 1, 3}。
样例输入2
3
1 3 1 2
2 1 0 0
样例输出2
0 0
样例输入3
6
1 3 0 1
1 2 0 2
2 4 1 0
4 5 1 0
5 6 0 2
样例输出3
1 4
什么破题,OJ上都没有!
讲解
首先我们可以很容易证明一个结论:每条边最多只会被翻转一次
为了讲解方便,我们令边权为0,1的边分别为不需要和需要翻转的边,2为无所谓的边
我们来从易到难解决问题
对于第四组数据,不用脑子,输出0即可
对于第三组数据,由于我们优先要满足操作次数少,所以我们要将被1边夹住的2边当做1边,而与0边相邻的2边当做0边,即可最优
对于第五组数据,是一个比较简单的树形DP
根据我们之前得到的结论,令dp[x]为使得x的子树内的边全部到达目标状态需要的操作数量和翻转长度
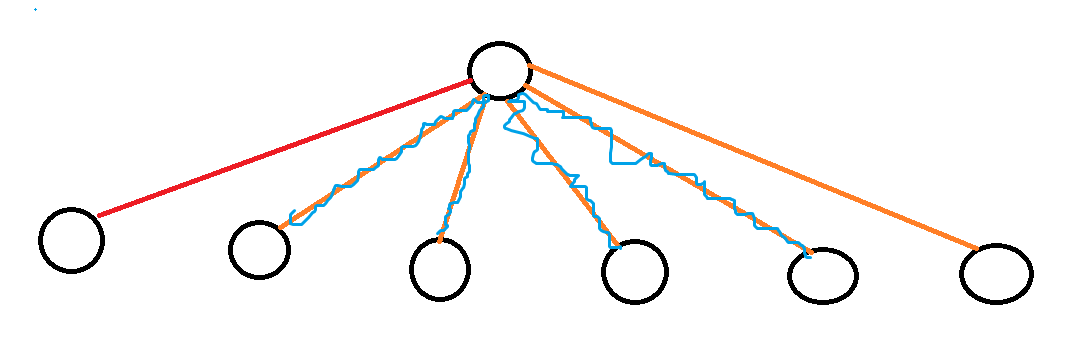
红色:不需要翻转的链,橙色:需要翻转的链
我们发现每两条需要翻转的链可以合并成一条,所以我们再用一个数组统计是否有从下面来的橙链,然后合并累加答案即可
对于第一组数据,我们可以枚举翻转的边,然后用上述方法求答案即可
对于第二组数据,同理,枚举是否翻转d=2的边,然后求答案
80pts了!
其实正解已经不远了,甚至跟部分分很相似
我们仍然可以从组合橙链来思考,令(dp[x][0/1])表示在节点x,是否翻转父边的答案(操作数与长度都要存)
转移详情见代码
代码
struct node
{
int f,len;
node(){}
node(int f1,int len1){
f = f1;
len = len1;
}
node operator + (const node &a){
return node(f+a.f,len+a.len);
}
bool operator < (const node &a)const{
if(f < a.f || (f == a.f && len < a.len)) return 1;
return 0;
}
}dp[MAXN][2];
int head[MAXN],tot;
struct edge
{
int v,w,nxt;
}e[MAXN << 1];
void Add_Edge(int x,int y,int z)
{
e[++tot].v = y;
e[tot].w = z;
e[tot].nxt = head[x];
head[x] = tot;
}
void Add_Double_Edge(int x,int y,int z)
{
Add_Edge(x,y,z);
Add_Edge(y,x,z);
}
void dfs(int x,int fa,int d)//当前节点,父节点,父边的翻转状态
{
node t1 = node(INF,INF),t2 = node(0,0);//t1:有剩余橙链,t2:无剩余橙;链
//这个循环是在组合子节点的状态
for(int i = head[x]; i ;i = e[i].nxt)
{
if(e[i].v == fa) continue;
dfs(e[i].v,x,e[i].w);
node tmp1 = Min(t1+dp[e[i].v][0],t2+dp[e[i].v][1]);//1条橙链与0条橙链,0条橙链与1条橙链 组合是1条橙链
node tmp2 = Min(t1+dp[e[i].v][1],t2+dp[e[i].v][0]);//1条橙链与1条橙链,0条橙链与0条橙链 组合是0条橙链
t1 = tmp1;
t2 = tmp2;
}
//更新父边不翻转状态 :
if(d == 1) dp[x][0] = node(INF,INF);
//父边必须被翻转,不能不翻,GG
else dp[x][0] = Min(node(t1.f+1,t1.len),t2);
//父边不一定被翻转,即可从 “有一条剩余橙链并把它翻转”与 “无剩余橙链 ”转移而来
//更新父边要翻转状态 :
if(!d) dp[x][1] = node(INF,INF);
//父边不能翻转,GG
else dp[x][1] = Min(node(t1.f,t1.len+1),node(t2.f+1,t2.len+1));
//父边不一定不翻转,即可从“与儿子的一条剩余橙边组合” 与 “无剩余橙链,翻转自己” 转移而来
}
int main()
{
// freopen("w.in","r",stdin);
// freopen("w.out","w",stdout);
n = Read();
for(int i = 1;i < n;++ i)
{
int u = Read(),v = Read(),c = Read(),d = Read();
if(d == 2) Add_Double_Edge(u,v,2);
else Add_Double_Edge(u,v,c^d);
}
dfs(1,0,2);
Put(dp[1][0].s >> 1,' ');Put(dp[1][0].len);
//由于我们在合并两条橙链的时候,两条链都被统计进了方案,但是我们是要合并的,所以要除以二
return 0;
}