前言(可跳过)
今天考试要用,而据说之前学过 完全没印象 ,特地前来补坑
真是 KCUF
正题
对于 (cp(n)) ((cp=)错排())
算了,还是叫它 (D(n)) 吧
如果对于 (1)~(n) 的序列,第一位填了 (x(2le xle n))
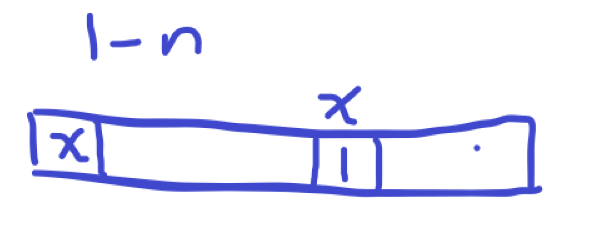
① 第 (x) 位填了1,那么剩下的 (n-2) 位就又转换为了相同的问题,而且有 (n-1) 种情况( (x) 有 (n-1) 种情况),所以这种情况总的就是 ((n-1) * D(n-2)) 如图:
② 第 (x) 位填的数字不是 (x) 也不是 (1)(否则就和上面重复了),那么我们现在就可以把 (1) 和 (x) 看成一个数了,因为一个没有数字,一个没有位置,老惨了
理解:就是现在的 (1) 不能填 (x) 的位置,其它的 (n-2) 个数字不能填它们对应的位置,所以就相当于 (1) 是 (x) 了(每个数字都有且仅有一个位置不能填)
剩下就是 (n-1) 个位置,第一个数 (x) 有 (n-1) 种情况,所以这种情况总的就是 ((n-1) * D(n-1)),如图:
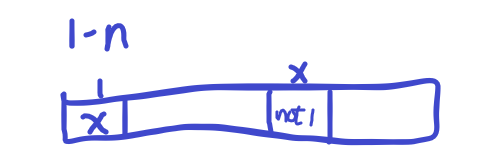
( herefore D(n) = (n-1) * left[D(n-1)+D(n-2) ight])
特别的:
(D(1) = 0)(1个数字,1个位置你怎么错排???)
(D(0) = 1)(错排即任何数字都没有在相应的位置上,没有数字当然就是一种排法)
结论
(D(n) = (n-1) * left[D(n-1)+D(n-2) ight])
(D(1) = 0)
(D(0) = 1)