2015 Multi-University Training Contest 2

多校第二场，赛后总共做出四题，总结的有点晚了，太懒，下面给出解题报告！！

Hdu 5301 Buildings

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5301

题意：有块地为n*m列的矩阵，要建造矩形公寓来完全覆盖这块地((x,y)方格除外)
　　且每个公寓必须有一边在这块地的矩阵的边缘上。
　　求满足条件的方案中公寓最大面积的最小值。

思路：相当于用矩形填充n*m的矩阵，且矩形至少有一条边在该矩阵的边界上
　　若不考虑(x,y)方格被删除，ans=(min(m,n)+1)/2;
　　删除(x,y)后，若 m=n且n为奇数，且(x,y)在中心点，ans=ans-1;
　　否则 如图：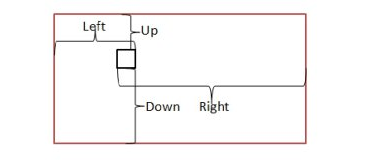

　　与(x,y)上下左右相邻点，只能往三个方向建公寓，对于这四个点
　　分别取对应的三个方向建公寓的最小面积s=min(s1,s2,s3);
　　ans=max(ans,s);

参考代码：

　　

#include<stdio.h>
#include<algorithm>
#define INF 999999999
const int dirX[4]={0,0,-1,1};
const int dirY[4]={1,-1,0,0};
using namespace std;
int main()
{
    int n,m,x,y;
    while(scanf("%d%d%d%d",&n,&m,&x,&y)!=EOF){
        int ans=(min(m,n)+1)/2;
        if(n%2&&m==n&&x==y&&x==(n+1)/2){
            printf("%d
",ans-1);
            continue;
        }
        for(int i=0;i<4;i++){
            int row=x+dirX[i];
            int col=y+dirY[i];
            int temp=INF;
            if(row>=1&&row<=n&&col>=1&&col<=m){
                if(row-1!=x)
                    temp=min(temp,row);
                if(row+1!=x)
                    temp=min(temp,n-row+1);
                if(col-1!=y)
                    temp=min(temp,col);
                if(col+1!=y)
                    temp=min(temp,m-col+1);
                ans=max(ans,temp);
            }
        }
        printf("%d
",ans);
    }
    return 0;
}

Hdu 5303 Delicious Apples

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5303

题意：一个环形道上有n个苹果树，第i棵树与仓库的顺时针距离为xi,树上有ai个苹果，仓库在位置0
　　你有一个容量为k的篮子，要从仓库出发去摘苹果，篮子装满后要回到起点清空篮子，
　　问你从起点出发，摘完所有苹果所走的最短路程。

思路：从起点可以顺时针或逆时针出发，最后的结果肯定是
　　顺时针取一定的苹果所走的最短路与逆时针走的最短路的和。

　　对于每棵树上的苹果，肯定是能现整取的先取完，然后回到原点，预处理一下，然后每棵树的苹果数就是原来的苹果数%k；

　　对于剩下的每个苹果离散化，每个苹果自成一个分量，

　　用sl表示左半圈苹果总数，用sr表示右半圈苹果总数。

　　用pl[]表示左半圈各个苹果距离远点的最短距离，pr[]表示右半圈苹果距离远点的最短距离。

　　用dpl[i]表示取左半圈的第i个苹果要走的最短路径，同理dpr[i]表示取右半圈的第i个苹果要走的最短路径。

　　ans=(dpl[sl-1]+dpr[sr-1])*2;//左边的都往左边运，右边的都往右边运得到的路程总和。

　　因为最多存在走一圈比分别走两边的短的情况，所以枚举每一个走全圈的情况，和ans比较大小，取小的那个；

参考代码：

 　　

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
struct node
{
    long long dis,x;
} left[100001],right[100001];
long long pl[100001],pr[100001];
long long dpl[100001],dpr[100001];
int cmp(node x,node y)
{
    return x.dis<y.dis;
}
int main()
{
    int T;
    int L,n,k;
    long long sum;
    long long ans;
    scanf("%d",&T);
    while(T--)
    {
        sum=0;
        long long a,b;
        int l=0,r=0;
        scanf("%d%d%d",&L,&n,&k);
        memset(pl,0,sizeof(pl));
        memset(pr,0,sizeof(pr));
        memset(dpl,0,sizeof(dpl));
        memset(dpr,0,sizeof(dpr));
        for(int i=0; i<n; i++)
        {
            scanf("%I64d%I64d",&a,&b);
            if(a*2<=L)
            {
                left[l].dis=a;
                left[l++].x=b;
            }
            else
            {
                right[r].dis=L-a;
                right[r++].x=b;
            }
        }
        sort(left,left+l,cmp);
        sort(right,right+r,cmp);
        for(int i=0; i<l; i++)
        {
            sum+=(left[i].dis)*(left[i].x/k)*2;
            left[i].x=left[i].x%k;
        }
        for(int i=0; i<r; i++)
        {
            sum+=(right[i].dis)*(right[i].x/k)*2;
            right[i].x=right[i].x%k;
        }
        //剩余的苹果离散化
        int sl=1;//左边苹果总数
        int sr=1;//右边苹果总数
        for(int i=0; i<l; i++)
        {
            if(left[i].x)
            {
                for(int j=0; j<left[i].x; j++)
                {
                    pl[sl++]=left[i].dis;
                }
            }
        }
        for(int i=0; i<r; i++)
        {
            if(right[i].x)
            {
                for(int j=0; j<right[i].x; j++)
                {
                    pr[sr++]=right[i].dis;
                }
            }
        }
        for(int i = 1; i < sl; i++)
        {
            if(i<=k)
                dpl[i]=pl[i];
            else
                dpl[i]=dpl[i-k]+pl[i];
        }
        for(int i = 1; i < sr; i++)
        {
            if(i<=k)
                dpr[i]=pr[i];
            else
                dpr[i]=dpr[i-k]+pr[i];
        }
        ans=(dpl[sl-1]+dpr[sr-1])*2;//左边的往左边运，右边的网友边运
        for(int i=0; i<=sl-1&&i<=k; i++)
        {
            int p1=sl-i-1;
            int p2=max(0,sr-1-(k - i));
            if(2*(dpl[p1] + dpr[p2])+L<ans)
                ans=2*(dpl[p1] + dpr[p2])+L;
        }
        printf("%I64d
",ans+sum);
    }
    return 0;
}

另一种方法更好理解：从起点可以顺时针或逆时针出发，最后的结果肯定是
　　顺时针取一定的苹果所走的最短路与逆时针走的最短路的和。
　　那么设dp[2][i]，0代表顺时针，1代表逆时针，i代表取的苹果数，
　　值为取完i个苹果回到原点的最短路程。x[i]为第i个苹果所在的位置。
　　以顺时针为例，如果2x[i] <L，那么后来走的路程为2x[i]，反之，为L；
转移方程：
　　dp[0][i] = min(dp[0][i],dp[0][i-j]+(2*x[i] <L ? 2*x[i] : L)) (1 <= j <= k)
　　因为dp[0][i]是非递减的,所以优化方程：
　　dp[0][i] = dp[0][i-k]+(2*x[i] <L ? 2*x[i] : L)

参考代码：

#include<stdio.h>
#include<algorithm>
#define INF 0x3fffffffffffffff
const int N=100010;
using namespace std;
struct stu{
    long long x,num;
}app[N];
long long L;
int n,k,sum;
long long dp[2][N];
int cmp(stu a,stu b)
{
    return a.x<b.x;
}
long long solve()
{
    dp[0][0]=dp[1][0]=0;
    int cnt=1;
    for(int i=1;i<=n;i++){     //顺时针
        for(int j=1;j<=app[i].num;j++){
            int t=cnt>k?cnt-k:0;
            dp[0][cnt++]=dp[0][t]+min(app[i].x*2,L);
        }
    }
    cnt=1;
    for(int i=n;i>=1;i--){     //逆时针
        for(int j=1;j<=app[i].num;j++){
            int t=cnt>k?cnt-k:0;
            dp[1][cnt++]=dp[1][t]+min((L-app[i].x)*2,L);
        }
    }
    long long ans=INF;
    for(int i=0;i<=sum;i++)
        ans=min(ans,dp[0][i]+dp[1][sum-i]);
    return ans;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%I64d%d%d",&L,&n,&k);
        sum=0;
        for(int i=1;i<=n;i++){
            scanf("%I64d%I64d",&app[i].x,&app[i].num);
            sum+=app[i].num;
        }
        sort(app+1,app+n+1,cmp);
        long long ans=solve();
        printf("%I64d
",ans);
    }
    return 0;
}

Hdu 5305 Friends

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5305

题意：有n个人，m组关系，表示谁和谁是朋友关系
　　朋友分为线上朋友和线下朋友，
　　求满足每个人的线上朋友数和线下朋友数相同
　　有多少种的情况

思路：题中n<=8，m<=n(n-1)/2，对于每组朋友关系
　　要么为线上，要么为线下，dfs加剪枝
　　要保证每个人线上朋友和线下朋友人数相等，
　　则每个人的朋友数都为偶数，且总边数m为偶数，否则输出0

参考代码：

　　

#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
using namespace std;
int n,m,sum;
struct node
{
    int x,y;
} fri[100];
int num[10];
int lf[10];
int rf[10];
void dfs(int p)
{
    if(p==m)
    {
        sum++;
        return;
    }
    int x=fri[p].x;
    int y=fri[p].y;
    if(lf[x]&&lf[y])
    {
        lf[x]--;
        lf[y]--;
        dfs(p+1);
        lf[x]++;
        lf[y]++;
    }
    if(rf[x]&&rf[y])
    {
        rf[x]--;
        rf[y]--;
        dfs(p+1);
        rf[x]++;
        rf[y]++;
    }
}
void work()
{
    int flag=0;
    for(int i=1; i<=n; i++)
    {
        lf[i]=num[i]/2;
        rf[i]=num[i]/2;
        if(num[i]%2)
        {
            flag=1;
            break;
        }
    }
    if(flag)
    {
        puts("0");
    }
    else{
        dfs(0);
        printf("%d
",sum);
    }
}
void input()
{
    int a,b;
    scanf("%d%d",&n,&m);
    for(int i=0; i<m; i++)
    {
        scanf("%d%d",&a,&b);
        fri[i].x=a;
        fri[i].y=b;
        num[a]++;
        num[b]++;
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        sum=0;
        memset(num,0,sizeof(num));
        input();
        work();
    }
    return 0;
}

Hdu 5308 I Wanna Become A 24-Point Master

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5308

题意：有n个数a1,a2…an,它们的值都为n
　　每次操作可以选两个未进行操作的数进行 “+”,”-“,”*”,”/“
　　第i次操作为a b c:其中a,c为数组下标，b为操作符， 则A[n+i]=A[a] b A[c];
　　要进行 n-1 次操作,使得最后数组2n-1的值为24
　　需要满足的条件：每个数都有且仅能用一次(包括新生成的数)
　　除法为小数除法，允许得到分数
　　若能找到满足条件的操作,输出这n-1次操作，否则输出-1

思路：

参考代码：

　　

#include<stdio.h>
int main()
{
    int N;
    while(scanf("%d",&N)!=EOF)
    {
        if(N<=3)
            printf("-1
");
        else if (N == 4)
        {
            printf("1 * 2
5 + 3
6 + 4
");
        }
        else if(N == 5)
        {
            printf("1 / 2
");
            printf("6 / 3
");
            printf("4 - 7
");
            printf("5 * 8
");
        }
        else if(N==6)
        {
            printf("1 + 2
");
            printf("3 + 7
");
            printf("4 + 8
");
            printf("9 // 5
");
            printf("10 * 6
");
        }
        else if(N == 7)
        {
            printf("1 + 2
");
            printf("3 + 8
");
            printf("9 / 4
");
            printf("5 / 6
");
            printf("11 + 7
");
            printf("10 * 12
");
        }
        else if(N == 8)
        {
            printf("1 + 2
");
            printf("3 + 9
");
            printf("4 - 5
");
            printf("11 * 6
");
            printf("12 * 7
");
            printf("13 * 8
");
            printf("10 + 14
");
        }
        else if(N == 9)
        {
            printf("1 + 2
");
            printf("3 + 4
");
            printf("11 + 5
");
            printf("12 + 6
");
            printf("13 + 7
");
            printf("14 + 8
");
            printf("15 / 9
");
            printf("10 + 16
");
        }
        else if(N == 10)
        {
            printf("1 + 2
");
            printf("11 / 3
");
            printf("4 + 12
");
            printf("6 + 5
");
            printf("14 + 7
");
            printf("8 + 15
");
            printf("9 + 10
");
            printf("16 / 17
");
            printf("13 * 18
");
        }
        else if(N == 11)
        {
            printf("1 + 2
");
            printf("12 / 3
");
            printf("4 / 5
");
            printf("6 + 14
");
            printf("7 - 8
");
            printf("16 * 9
");
            printf("17 * 10
");
            printf("18 * 11
");
            printf("13 * 15
");
            printf("20 + 19
");
        }
        else if(N == 12)
        {
            printf("1 + 2
");
            printf("3 - 4
");
            printf("14 * 5
");
            printf("6 * 15
");
            printf("7 * 16
");
            printf("8 * 17
");
            printf("9 * 18
");
            printf("10 * 19
");
            printf("11 * 20
");
            printf("12 * 21
");
            printf("13 + 22
");
        }
        else
        {
            if(N%2==0)
            {
                printf("1 + 2
");
                int p=3,q=N+1;
                for(int i=1; i<3; i++)
                {
                    printf("%d + %d
",p++,q++);
                }//加三次N
                printf("%d / %d
",q++,p++);//除以N得到4
                printf("%d + %d
",p,p+1);//得到2倍的N
                int cnt1=q++;
                p+=2;
                for (int i=1; i<5; i++)
                {
                    printf("%d + %d
",p++,q++);
                }//得到6倍的N
                printf("%d / %d
",q++,p++);//得到6
                int cnt2=q++;
                while (p<N)
                {
                    printf("%d / %d
",p,p+1);//得到0
                    p+=2;
                    q++;
                    printf("%d * %d
",q-1,cnt1);
                    cnt1=q++;
                }
                printf("%d * %d
",cnt1,cnt2);//4*6=24
            }
            else
            {
                printf("1 + 2
");
                int p=3,q=N+1;
                for (int i=1; i<2; i++)
                {
                    printf("%d + %d
",p++,q++);
                }
                printf("%d / %d
",q++,p++);//得到3
                printf("%d + %d
",p,p+1);
                int cnt1=q++;
                p+=2;
                for (int i=1; i<7; i++)
                {
                    printf("%d + %d
",p++,q++);
                }
                printf("%d / %d
",q++,p++);//得到8
                int cnt2=q++;
                while (p<N)
                {
                    printf("%d / %d
",p,p+1);
                    p+=2;
                    q++;
                    printf("%d * %d
",q-1,cnt1);
                    cnt1=q++;
                }
                printf("%d * %d
",cnt1,cnt2);//3*8=24
            }
        }
    }
    return 0;
}