1.功能概述
数据拉伸与显示属于图像增强,主要用于改变图像的显示效果,突出了特定的图像特征,以提供最佳的影像视觉效果,用于制图出图或为影像目视解译提供合适的素材。


2.基本概念
2.1 基本概念——亮度
图像亮度,是指图像的明暗程度,通过调整影像数据的显示亮度来增强影像中地物之间的差异。
- 图像亮度增加时,就会显得夺目或刺眼;
- 图像亮度减小时,就会显得灰暗或暗淡。



低亮度 中亮度 高亮度
2.2 基本概念-对比度
对比度,指的是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量,差异范围越大代表对比越大,差异范围越小代表对比越小。
- 一般来说对比度越大,图像越清晰醒目,色彩也越鲜明艳丽;
- 而对比度小,则会让整个画面都灰蒙蒙的,很难看清楚影像中地物之间的差异。

2.3 基本概念-透明度
图像透明度是相对的,通过透明度增强用来调整影像显示的透明程度以增强影像中地物之间的差异。


原始影像 透明度增强后
2.4 基本概念-图像拉伸
图像拉伸增强能够:
- 改善图像对比度
- 突出感兴趣的地物信息
- 提高图像目视解译效果


拉伸前 拉伸后
2.4.1 基本概念——图像拉伸:线性拉伸
线性拉伸(灰度拉伸),是对单波段逐个像元进行处理,将原图像的亮度值动态范围按照线性关系式扩展至指定范围或整个动态范围。
假设原图像f(x、y)的灰度范围为[a,b],线性变换后图像g(x、y)范围为[a',b']。g(x、y)与f(x、y)之间的关系式为:
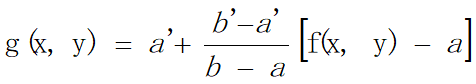
根据a和b不同的取值,可以进行按照百分比的线性拉伸:
- 1%线性拉伸:a取累计直方图的1%,b取累计直方图的99%
- 2%线性拉伸:a取累计直方图的2%,b取累计直方图的98%
- 3%线性拉伸:a取累计直方图的3%,b取累计直方图的97%
- 5%线性拉伸:a取累计直方图的1%,b取累计直方图的95%
2.4.2 基本概念——图像拉伸:直方图均衡化
- 基本原理:一般遥感图像的概率密度函数曲线是一个起伏的曲线,直方图均衡化就是将变换后的图像的概率密度函数变为平坦的直线,将原图像的直方图通过变换函数修正为均匀的直方图,然后按均衡直方图修改原图像。
- 基本思想:对原始图像的像素灰度做某种映射变换,使变换后图像灰度的概率密度呈均匀分布,即变换后图像的灰度级均匀分布。这意味着图像灰度的动态范围得到了增加,从而提高了图像的对比度。
- 用途:通常用来增加图像的全局对比度,尤其是当图像有用数据的对比度相当接近的时候。亮度可以更好地在直方图上分布,这样既可以用于增强局部的对比度而不影响整体的对比度。这种方法对于背景和前景都太亮或者太暗的图像非常有用。
- 优势:它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,计算量也不大。
- 缺点:它对处理的数据不加选择,可能会增加背景噪声的对比度并且降低有用信号的对比度。
2.4.3 基本概念——图像拉伸:标准差拉伸
标准差拉伸通过修剪影像极值,然后对其他像素值进行线性拉伸来使影像的对比度增加。
标准差反应组内个体的离散度:
- 标准差大,表示组内大多数数值和平均值偏离的越多;
- 标准差小,表示组内大多数数值和平均值比较接近。
在图像处理中,如果设置标准差为2,那么超过两个标准差的像素值会被推到0或者255的位置,两个标准差之间的像素值被线性拉伸至0到255。

2.4.4 基本概念——图像拉伸:最大最小值
最大最小值拉伸可以自由设置最大最小值,然后以最大值和最小值为两个端点。然后再对像素值进行线性拉伸,使得影像更易区分。最大最小值拉伸一般适用于拉伸像素值分布密集的栅格影像。
2.5 基本概念-亮度反转
亮度反转操作可反转显示图像的明亮度。产生一幅与输入影像相反的影像,原来亮的地方变暗,原来暗的地方变亮。


反转前 反转后
2.6 基本概念-透明值
影像加载后,影像边缘部分一般会存在黑边(无效值),通过添加设置的透明值域对栅格影像的显示进行控制,以提高图像的显示效果。
- 将透明值区间设置成0-0,就可以把无效值(0值)全部透明处理。


设置前 设置后
2.7 基本概念-重置
重置:可将当前图层恢复到原始状态。
3.演示数据
操作流程:
选用一景遥感栅格影像,使用"显示控制"下的【亮度增强】、【对比度增强】、【透明度增强】、【拉伸增强】、【亮度反转】、【透明值】、【重置】功能。
使用数据:
GF1_PMS1_E116.5_N39.4_20131127_L1A0000117600-MSS1.tiff
4.操作演示
4.1操作演示——亮度增强
操作方法:
- 向左或向右移动滑动条,来调整影像数据的显示亮度;
- 点击【亮度】按钮即可恢复默认值。

4.2 操作演示——对比度增强
操作方法:
- 向左或向右移动滑动条,可调整图层的对比度;
- 点击【对比度】按钮即可恢复默认值。

4.3操作演示——透明度增强
操作方法:
- 向左或向右移动滑动条,可调整图层的对透明度;
- 点击【透明度】按钮即可恢复默认值。

4.4操作演示——自动拉伸增强
操作方法:
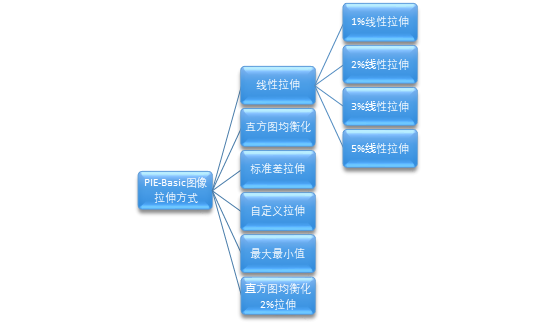
- "显示控制"下的【拉伸增强】功能,包括线性拉伸(1% /2% /3% /5%)、直方图均衡化、标准差拉伸、自定义拉伸、最大最小值和直方图均衡化2%拉伸九种拉伸方式。
- 除"自定义拉伸"以外,其余均为自动拉伸,点击相应按钮即可进行拉伸操作。
- 目前PIE软件在加载影像时都自动采用了2%线性拉伸。
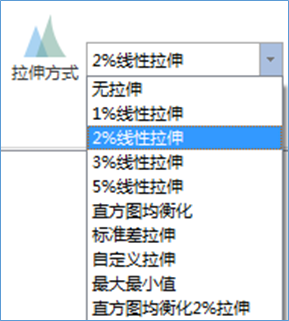

4.5操作演示——自定义拉伸(手动拉伸)增强
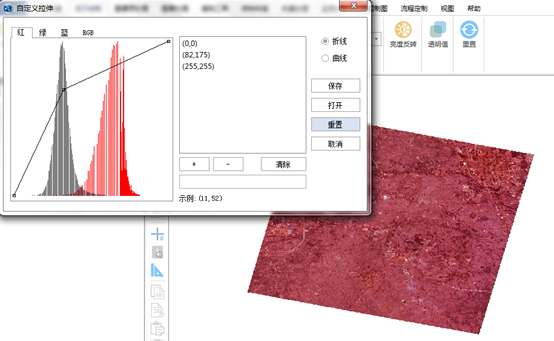
在"拉伸方式"的下拉列表中选择【自定义拉伸】,打开【自定义拉伸】对话框:
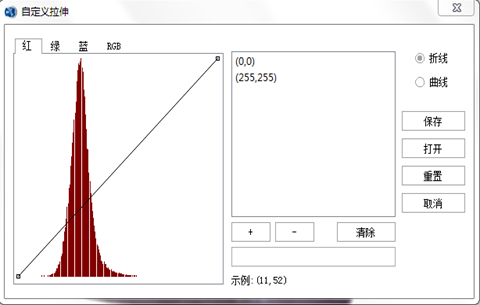
- 颜色通道:选择待拉伸的四个颜色通道(红、绿、蓝、RGB);
- 直方图窗口:在直方图上单击即可添加节点,也可通过右侧的节点值窗口自定义设置拉伸节点;
- 拉伸节点值窗口:显示拉伸折线或曲线的节点值坐标;
- 点击【+】按钮,即可将该节点添加到拉伸的节点,同时直方图实时拉伸;
- 点击【-】按钮,即可将选中的节点删除;
- 清除:可将拉伸节点值窗口中新增的节点值全部清除,恢复到初始状态。
- 线形:设置自定义拉伸方式为折线型或曲线型;
- 保存:设置拉伸后直方图的保存路径与文件名,即可将拉伸后的直方图进行保存;
- 打开:打开文件夹,可直接导入已有的自定义设置;
- 重置:当前波段恢复到没有任何拉伸效果时的状态;
- 取消:取消拉伸直方图操作。
在【自定义拉伸】对话框中调整拉伸的数据范围及拉伸方式,拉伸效果可在视图中实时显示。
4.6操作演示——亮度反转
操作方法:
点击【亮度反转】按钮,即可对当前图层执行亮度反转操作。

4.7操作演示——透明值
在"显示控制" 标签下单击【透明值】按钮,打开【自定义透明度】对话框:

- 添加透明值域:输入透明值域的最大值和最小值;
- 添加:设置透明值域信息后,点击【添加】按钮,将透明值域加载到左侧列表中,可增加多组透明值域;
- 删除:选中左侧列表中的数值组,点击【删除】按钮,删除选中的信息;
- 修改:单击列表中添加的透明值范围,可在最大最小值输入框中重新输入值,点击【修改】按钮,即可对选中的透明值范围进行更改。
选中列表中的值域信息,点击【确定】按钮,对栅格数据的像素值在选中的值域范围内的进行透明显示,并且关闭图层属性对话框;点击【取消】按钮,不对栅格数据进行透明显示,并且关闭图层属性对话框。

4.8操作演示——重置
操作方法:
点击【重置】按钮,即可将当前图层恢复到原始状态。
