Catalan数

一、递推式

已知n（n∈N）个元素，约定元素k表示第k个入栈的元素，换句话说，将元素按入栈顺序的先后编号为1_{n，称为元素1}n。求可能的出栈顺序的总数C_n。
显然C₁=1, C₂=2。当n=3时，C₃=5，可能的出栈顺序有（用1表示入栈，0表示出栈）

出栈顺序	123	132	213	231	321
操作方法	101010	101100	110010	110100	111000

如当n=4时，C₄=14，可能的出栈顺序有

出栈顺序	1234	1243	1324	1342	1432	2134	2143
操作方法	10101010	10101100	10110010	10110100	10111000	11001010	11001100
出栈顺序	2314	2341	2431	3214	3241	3421	4321
操作方法	11010010	11010100	11011000	11100010	11100100	11101000	11110000

将这14种可能按照元素1的出栈顺序可以分成4组：元素1第1/2/3/4个出栈。

出栈顺序	1234	1243	1324	1342	1432	2134	2143
操作方法	10101010	10101100	10110010	10110100	10111000	11001010	11001100
出栈顺序	2314	2341	2431	3214	3241	3421	4321
操作方法	11010010	11010100	11011000	11100010	11100100	11101000	11110000

不妨按元素1第几个出栈排列。当元素1第1个出栈时，**元素234的出栈顺序任意**，方案数显然为C₃。当元素1第2个出栈时，显然第1个出栈的是元素2，后2个出栈的便为元素34，且**只要元素34出栈顺序合法，则4个元素的出栈顺序便一定为合法的**，根据分步相乘原则，方案数为C₁×C₂；当元素1第3个出栈时，显然前2个出栈的是元素23，最后一个出栈的是元素4，方案数为C₂×C₁；当元素1第4个出栈时，前3个出栈的元素234顺序任意，方案数也为C₃。最后，根据分组相加原则，总方案数C₄=C₃+C₁×C₂+C₂×C₁+C₃。 推广到C_n，可得Catalan数的递推式： $$box[#CCF]{C_n=egin{cases}0, & n=0 \ displaystylesum_{k=0}^{n}{C_kC_{n-k}}, & n>0end{cases}}$$ ##二、通项公式 求$C_n$的通项公式则是由操作方法的01串入手。首先，显然对于每个合法的01串，在其任意前缀中1的数量$≥$ 0的数量。每个元素都会入栈一次、出栈一次，则01串必然有2n个数字，由n个0和n个1组成。在2n个位置中填入n个1（剩下的位置自动填0）的方案数为$C_{2n}^n$。从$C_{2n}^n$中减去不合法的方案数即为所求。同理，对于每个不合法的01串，必然在至少一组前缀中1的数量<0的数量。 对于每个不合法的01串，设m为0的数量>1的数量的最短前缀中1的个数，显然该前缀有m个1，m+1个0和2m+1个数位。此后的2(n-m)-1位上有n-m个1，n-m-1个0。如果把这2(n-m)-1位按位取反，变为n-m个0，n-m-1个1，结果得到一个由n+1个0和n-1个1组成的2n位01串。 反过来，任何一个由n+1个0，n-1个1组成的2n位01串，也必然在某一前缀中0的数量>1的数量，同样将后面的数位按位取反，结果得到一个由n个0和n个1组成的2n位01串，且由于两个01串的前缀相同，∴新01串必然在同一前缀中0的数量>1的数量，∴新01串一定是不合法的。 通过上述过程，我们证明了由n个0和n个1组成的2n位不合法01串与由n+1个0和n-1个1组成的2n位01串**一一对应**，所以不合法的01串共有$C_{2n}^{n+1}$个。 $$egin{align*}∴C_n&=C_{2n}^n- C_{2n}^{n+1}\&=cfrac{(2n)!}{n!n!}-frac{(2n)!}{(n+1)!(n-1)!}\&=(2n)!left[cfrac{1}{n!n!}-cfrac{1}{(n+1)!(n-1)!} ight]\&=(2n)!left[cfrac{n+1}{(n+1)!n!}-cfrac{n}{(n+1)!n!} ight]\&=cfrac{(2n)!}{(n+1)!n!}\&=cfrac{(2n)!}{(n+1)n!n!}\&=cfrac{C_{2n}^n}{n+1}end{align*}$$$$box[#CCF]{C_n=cfrac{C_{2n}^n}{n+1}}$$ ##三、问题归约 Catalan数的变式很有趣的一点是推出递推式与通项公式的方法不同，可归约到该方法的问题也不同。 易归约到推出递推式的方法的问题包括 1. C_n表示通过连结顶点而将凸(n + 2)边形分成三角形的方案数。  2. C_n表示用n个长方形填充一个有n个台阶的阶梯的方案数。  3. C_n表示有n个结点组成二叉树的方案数。  4. C_n表示有2n+1个节点组成不同构满二叉树的方案数。  5. C_n表示在圆上有2n个点，将这些点两两连接成n条互不相交的弦的方案数。 **分析** 将这2n个点顺时针编号为0, 1, ..., (2n-1)（从哪个点开始编号任意）。按点0连接的**编号最小**的点的编号分类，显然这个点的编号可能为1, 3, 5...但不可能是2, 4, 6...。如果点0连接编号为偶数的点，无论顺时针还是逆时针数中间必然夹了奇数个点。而连接编号为奇数的点时，设该点编号为2k-1，易计算出顺时针数在编号1~2k-2间有k-1条弦，则编号2k~2n-1间有n-k条弦。

易归约通项公式的方法的问题包括

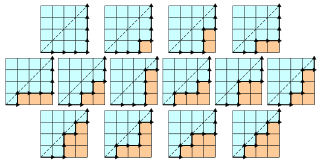
1. C_n表示在平面直角坐标系中，只向右、向上走，只在格点处转弯，对于路径上任意格点的坐标(x,y)，均有x(≥)y，从(0,0)走到(n,n)的方案数。
   
2. C_n表示在圆上有2n个点，将这些点两两连接成n条互不相交的弦的方案数。
   分析（TODO）
3. C_n表示2n个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，求排列方式的方案数。
4. C_n表示2n个人排队买票，票价为50元，其中n人只有一张50元，另外n人只有一张100元，初始时售票窗口没有钱，一人只买一张票，求能够让售票处找得开钱的排队顺序的方案数。

四、变式

1. 有n条入栈指令，m条出栈指令，n(≥)m，求合法的指令序列的方案数。
   分析 显然含n条入栈指令，m条出栈指令的总数为(C_{n+m}^{n})。同理，对于每个合法的01串，在其任意前缀中1的数量≥0的数量；对于每个不合法的01串，必然在至少一组前缀中1的数量<0的数量。对于每个不合法的01串，设v为0的数量>1的数量的最短前缀中1的个数，显然该前缀有v个1，v+1个0和2v+1个数位。此后的(n+m-2v-1)位上共有n-v个1和m-v-1个0。按位取反后，共有n-v个0和m-v-1个1，最终得到一个由n+1个0和m-1个1组成的01串。同理，由n+1个0和m-1个1组成的01串也可以转化成一个不合法的01串。于是便建立了由n+1个0和m-1个1组成的01串同不合法01串的一一对应。∴所以不合法的01串共有(C_{n+m}^{n+1})个。∴合法方案数为$$C_{n+m}^{n}-C_{n+m}{n+1}=frac{n-m+1}{n+1}C_{n+m}^{n}$$
2. n+m个人排队买票，n(≥)m，票价为50元，其中n人只有一张50元，另外m人只有一张100元，初始时售票窗口没有钱，一人只买一张票，求能够让售票处找得开钱的排队顺序的方案数。
3. 在平面直角坐标系中，只向右、向上走，只在格点处转弯，对于路径上任意格点的坐标(x,y)，均有x(≥)y，从(0,0)走到(n,m)的方案数，n(≥)m。