趾压板矩阵
时间限制: 1 Sec 内存限制: 128 MB
[提交] [状态]
题目描述
第二天早晨,跑男队员们来到了风景秀丽的扬州瘦西湖,刚下车他们全都尖叫起来,没错,就是他们最怕的“趾压板”:
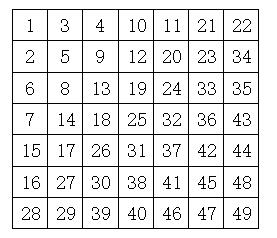
一块超级大的趾压板被分成了n行n列,每个小格子上都有一个数字。游戏规则是:观察一段时间后,把所有的数字拿掉,分别抽取一个行号i和列号j,说出这个位置上原来的数字是多少,如果不能说出正确的值,就要接受处罚,光脚从左上角1沿着顺序从小到大走到这个数字所在位置。
“捡漏王”王祖蓝思考了一会,马上找到了其中的奥秘,你呢?
输入
输入共一行,包含三个整数n,i,j,每两个整数之间用空格隔开,分别表示矩阵大小、待求的数所在的行号和列号。
输出
输出共一行,包含一个整数,表示相应矩阵中第i行和第j列的数。
样例输入 Copy
7 4 3
样例输出 Copy
18
提示
对于50%的数据,1≤n≤100;
对于100%的数据,1≤n≤30,000,1≤i≤n,1≤j≤n。
主要是太菜了所以只会很笨的找规律
以下是分析这个题的三个过程:
1.
因为以前做过类似的,是计算上三角的一个题,所以很自然的可以想到先判断这个数的斜对角线上对应的第一列的数是多少,再根据奇数行相减,偶数行相加可以很容易的算出一部分数。这样可以拿到55分。
2.
这样只适合于i+j<n的情况,如果i+j>n的话,会一直延伸计算,这样的第一列所对应的数的行数就会大于n。
然后可以发现,如果i+j-1>=n 时,是跟最后一行的数在同一个斜对角线上,这时候也是奇数列相减,偶数列相加的规律,可以算出上三角的一部分数。这样是91。
坑就坑在91,为什么偶数行的样例不能多一点(自闭.jpg)
3.
随便试一个偶数就会发现上述规律不存在了,然后也就有了代码里的
if(k%2==n%2)
判断是不是跟n同奇偶性。
历经波澜啊简直
代码:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
int main(){
ll n,i,j;
cin>>n>>i>>j;
ll res=0;
ll m=i+j-1;
if(m<n){
for(ll k=1;k<=i+j-1;k++){
if(k%2==0||k==1) res++;
else res+=k/2*4;
}
if((i+j-1)%2) res-=j-1;
else res+=j-1;
cout<<res<<endl;
}
else{
///计算a[n][i+j-n]
ll tmp=n*n;
ll cnt=0;
for(ll k=n;k>i+j-n;k--){
if(k%2==n%2) tmp-=2+4*cnt,cnt++;
else tmp--;
}
/// cout<<tmp<<endl;
ll tmp1=i+j-n;
if(tmp1%2==n%2) tmp-=n-i;
else tmp+=n-i;
cout<<tmp<<endl;
}
return 0;
}
放一个更简洁的代码
巨巨博客:传送门
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,x,y;
cin>>n>>x>>y;
int tmp=x+y-1;//位于第几层
int cnt=tmp-1;
int sum1=0,ans=0;
for(int i=1;i<=cnt;i++)
{
if(i<=n)
sum1+=i;
else sum1+=n-(i%n);
}
ans=sum1;
//cout<<ans<<endl;
if(tmp%2==0)
{
if(tmp<=n) ans+=y;
else if(tmp>n) ans+=y-(tmp-n);
}
else{
if(tmp<=n) ans+=tmp-y+1;
else if(tmp>n) ans+=x-(tmp-n);
}
cout<<ans<<endl;
return 0;
}