团体程序设计天梯赛练习集 PAT-L3-009 长城 凸包

题目链接：https://www.patest.cn/contests/gplt/L3-009

这道题拖了好久才AC掉。之前想的好几种贪心思路都是错的，不过也能拿26分。（测试点分值的分布好诡异……）

错误的贪心思路之一：从右往左处理时，只考虑上一个监视点。可以构造出这样一个反例：

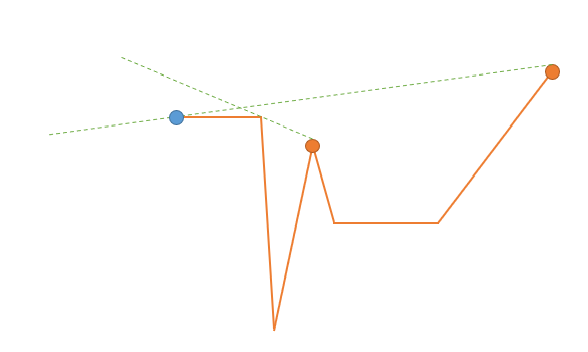
蓝色的点不能被左边的监视点覆盖，但可以被右边的监视点覆盖。

本题的正解是：维护一个上凸的半凸包：

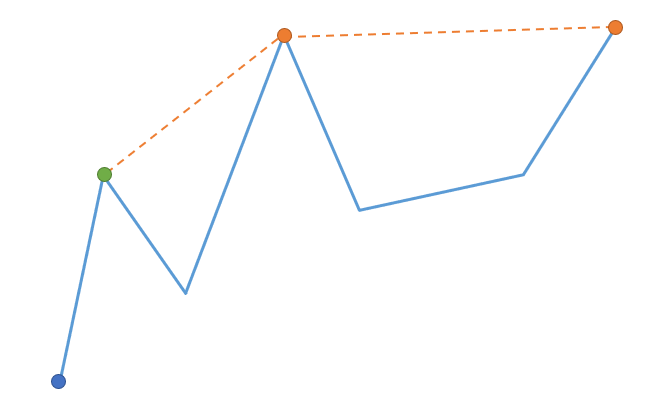
截止到绿色节点时，凸包的形状如黄色虚线所示，两个黄色节点是监视点。

然后我们继续向左处理，当前节点（蓝色）可以直接加入凸包，而不需要移除其中任何节点。因此不难发现，现有的两个监视点不能覆盖当前位置，我们必须将绿色节点也设为监视点。

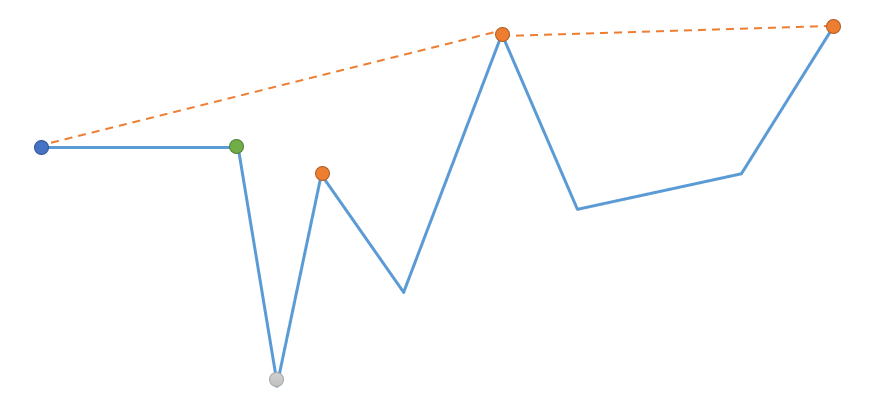
继续向左，将当前节点加入凸包时需要移除其中两个节点，如下图：

由图可知当前节点可以被监视。

继续这个过程：

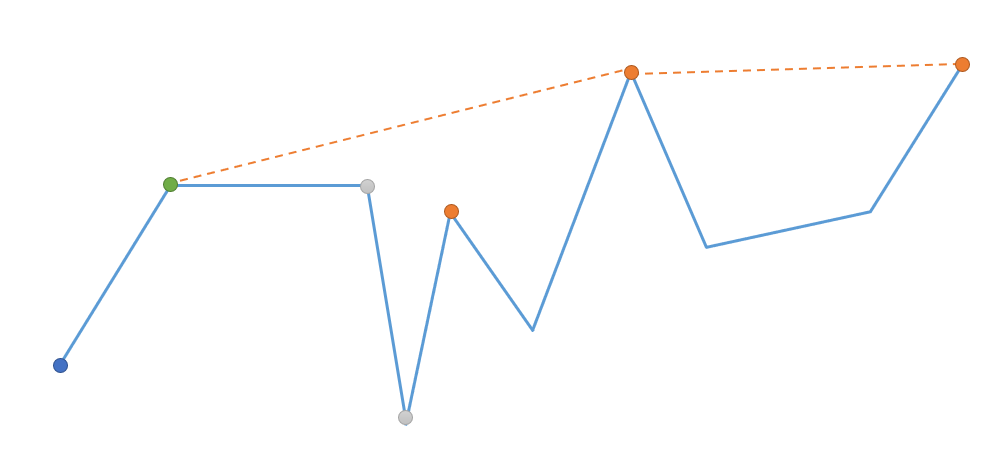
最后一张图时，将当前节点加入凸包不需要移除其中任何节点，说明当前位置无法受监视，需要将绿色节点也设为监视点。

综上可知，在维护上凸的半凸包时，如果加入某个节点不会导致凸包里其他节点被移除，那么之前一个节点就应该被设为监视点，答案+1。

代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

struct Point { int x, y; };

vector<Point> stk;
int ans = 0;
int N;

long long multi(int x1, int y1, int x2, int y2)
{
    return 1LL * x1 * y2 - 1LL * x2 * y1;
}

int main()
{
    int x, y, lx, ly;
    scanf("%d", &N);
    scanf("%d%d%d%d", &x, &y, &lx, &ly);
    stk.push_back({x, y});
    stk.push_back({lx, ly});

    for (int i = 3; i <= N; i++)
    {
        scanf("%d%d", &x, &y);
        bool ok = false;
        while (stk.size() >= 2)
        {
            Point &p1 = stk.back();
            Point &p2 = stk[stk.size() - 2];
            if (multi(p1.x - p2.x, p1.y - p2.y, x - p1.x, y - p1.y) <= 0)
            {
                ok = true;
                stk.pop_back();
            }
            else break;
        }
        if (!ok)
            ans += 1;
        stk.push_back({x, y});
    }

    printf("%d", ans);
    return 0;
}