《算法图解》第八章_贪婪算法_集合覆盖问题

一、贪婪算法介绍

算法基本思路：从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。（摘自 贪婪算法_百度百科）

简单直接的描述，就是指每步都选择局部最优解，最终得到的就是全局最优解。

二、引入：集合覆盖问题

假设你办了个广播节目，要让全美个州的听众都收听得到，为此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，因此你试图在尽可能少的广播台播出。现有广播台名单如下：

每个广播台都覆盖特定的区域，不同广播台的覆盖区域可能重叠。

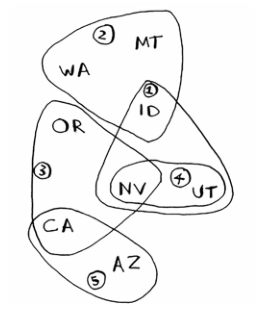
如何找出覆盖全美个州的最小广播台合集呢？下面是解决步骤：

1. 列出每个可能的广播台集合，这被称为幂集（power set）。可能的子集有2ⁿ个。
2. 在这些集合中，选出覆盖全美50个州的最小集合。

那么问题来了，计算每个可能的广播台子集需要很长的时间。

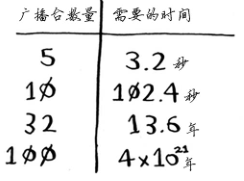
我们可以尝试使用贪婪算法。

三、算法实现

算法步骤

1. 选出这样一个广播台，即它覆盖了最多未覆盖的州。即便这个广播台覆盖了一些已覆盖的州（就是重复覆盖），也没有关系。
2. 重复第一步，直到覆盖了所有的州。

这是一种近邻算法（approximation algorithm）。在获得精确解需要的时间太长时，可以考虑使用近似算法。判断近似算法优劣的标准如下：

• 速度有多快；
• 得到的近似解与最优解的接近程度。

因此贪婪算法是一个不错的选择，它们不仅简单，而且通常运行速度很快。在本例中，贪婪算法的运行时间为O(n²)，其中n为广播台数量。

代码如下

# 创建一个列表，其中包含要覆盖的州
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) # 传入一个数组，被转换为集合

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set() # 使用一个集合来存储最终选择的广播台

while states_needed:
  best_station = None # 将覆盖了最多的未覆盖州的广播台存储进去
  states_covered = set() # 一个集合，包含该广播台覆盖的所有未覆盖的州
  for station, states in stations.items(): # 循环迭代每个广播台并确定它是否是最佳的广播台
    covered = states_needed & states # 计算交集
    if len(covered) > len(states_covered): # 检查该广播台的州是否比best_station多
      best_station = station # 如果多，就将best_station设置为当前广播台
      states_covered = covered

  states_needed -= states_covered # 更新states_needed
  final_stations.add(best_station) # 在for循环结束后将best_station添加到最终的广播台列表中

print(final_stations) # 打印final_stations

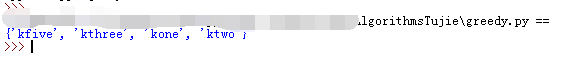
四、小结

• 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
• 贪婪算法易于实现、运行速度快，是不错的近似算法。
• 广度优先搜索、迪杰斯特拉算法是贪婪算法。

五、代码部分解读

在上述算法中，有一段代码很有趣

covered = states_needed & states # 计算交集

它是用来进行集合之间的相关计算，在此介绍下并集、交集和差集

• 并集意味着将集合合并；
• 交集意味着找出两个集合中都有的元素；
• 差集意味着将从一个集合中剔除出现在另一个集合中的元素。

下面将举例进行说明

>>> fruits = set(["avocado","tomato","banana"])
>>> vegetables = set(["beets","carrots","tomato"])
>>> fruits | vegetables # 计算并集
{'carrots', 'tomato', 'avocado', 'beets', 'banana'}
>>> fruits & vegetables # 计算交集
{'tomato'}
>>> fruits - vegetables # 计算差集
{'avocado', 'banana'}
>>> vegetables - fruits
{'carrots', 'beets'}

 

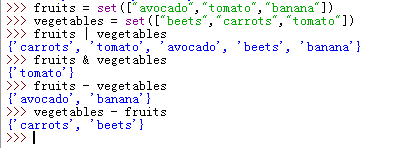
由此我们可以看出，集合类似于列表，只是不能包含重复的元素。