隔热板

隔热板

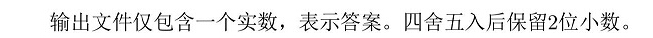
题目大意

给定平面直角坐标系上的$N$个点，让你画$m$条直线使得每一个点与原点的连线都与这$m$条直线至少有$1$个交点，求这$m$条直线到原点距离的最小值的最大值。

题解

由于题目求最小值的最大值，满足二分性质，考虑将已成立的$m$条直线向原点平移若干个单位，一定仍满足要求。

所以考虑二分答案，以原点为圆心，二分出的答案为半径画圆，显然这$m$条直线均与圆相切时最优。

考虑一个点$P$与原点的连线被截，当且仅当该点在园外且$m$条直线中至少有一条满足其切点在$P$向圆引切线形成的两个切点所构成的劣弧上。

那么就把问题转化成了若干个形如“在一段弧上至少选一个点”的要求，就变成了一个环上的区间选点问题，可以类似SCOI2015 国旗计划一样先判重复区间再倍增解决。

复杂度$O(Nlog Nlog Dis{(X_i,Y_i),(0,0)})$

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define DB double
#define LL long long
#define M 160020
using namespace std;
int read(){
	int nm=0,fh=1; int cw=getchar();
	for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
	for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
	return nm*fh;
}
int n,m,od[M],vis[M],nt[M][19];
const DB pi=acos(-1); bool vs[M];
DB l[M],r[M],X[M],Y[M],D[M],R=100000000.0,L,md,ans;
DB a1[M],a2[M],p1[M],p2[M];
bool cmp(int x,int y){return p2[x]<p2[y]||(p2[x]==p2[y]&&p1[x]>p1[y]);}
bool CMP(int x,int y){return a2[x]<a2[y];}
int check(DB dis){
	DB last=-pi*6; int tot=0,cnt=0,res=n;
	for(int i=1;i<=n;i++){
		DB t1=acos(X[i]/D[i]),t2=acos(dis/D[i]); if(Y[i]<0.0) t1=pi+pi-t1;
		if(t1-t2<0.0) t1+=pi+pi; l[i]=t1-t2,r[i]=t1+t2;
		tot++,p1[tot]=l[i]-pi-pi,p2[tot]=r[i]-pi-pi,vis[tot]=i,od[tot]=tot;
		tot++,p1[tot]=l[i],p2[tot]=r[i],vis[tot]=i,od[tot]=tot;
		tot++,p1[tot]=l[i]+pi+pi,p2[tot]=r[i]+pi+pi,vis[tot]=i,od[tot]=tot;
	} sort(od+1,od+tot+1,cmp),memset(vs,false,n*2); 
	for(int i=1;i<=tot;i++){
		int x=od[i];
		if(last>=p1[x]) vs[vis[x]]=true;
		else last=p1[x];
	}
	
	for(int i=1;i<=n;i++){
		if(vs[i]) continue;	cnt++,a1[cnt]=l[i],a2[cnt]=r[i],od[cnt]=cnt;
		cnt++,a1[cnt]=l[i]+pi+pi,a2[cnt]=r[i]+pi+pi,od[cnt]=cnt;
	} sort(od+1,od+cnt+1,CMP),nt[cnt+1][0]=cnt+1;
	for(int i=1,RS=2;i<=cnt;i++){while(RS<=cnt&&a1[od[RS]]<=a2[od[i]]) RS++; nt[i][0]=RS;}
	for(int k=1;k<17;k++) for(int i=1;i<=cnt+1;i++) nt[i][k]=nt[nt[i][k-1]][k-1];
	for(int i=1;i<=(cnt>>1);i++){
		int now=i,num=0;
		for(int k=16;k>=0;k--){
			if(nt[now][k]<=cnt&&nt[now][k]<i+(cnt>>1)){
				now=nt[now][k],num|=(1<<k);
			}
		} res=min(res,num+1);
	} return res;
}
int main(){
	n=read(),m=read(),L=0.00001;
	for(int i=1;i<=n;i++){
		X[i]=(DB)read(),Y[i]=(DB)read(),od[i]=i,od[i+n]=i+n;
		R=min(R,D[i]=sqrtl(X[i]*X[i]+Y[i]*Y[i]));
	}
	while(L+0.00001<R){
		md=(R+L)*0.5;
		if(check(md)<=m) L=md,ans=md;
		else R=md;
	} printf("%.2lf
",ans); return 0;
}