类似于区间树,在各个节点保存的是一条线段(子数组),可高效解决连续区间动态查询问题。
*单点或区间的修改 区间的最值以及求和
可基本保持单次操作为log的复杂度。
线段树的每个节点表示一个区间,子节点则分别表示父亲节点的左半区间和右半区间。如果父亲节点是[a,b],那么令c = (a+b) / 2,有左儿子[a,c],右儿子[c+1,b]。
可以用来求解形似下面的问题:
给定一个数列,要求你查找某个区间内的最小值,支持元素的更新。
朴素的做法显然,但是时间复杂度高达O(n),尽管所需额外空间复杂度只有O(1),但时间复杂度增长太高,这是我们不能接受的。
还有一种做法是用一个二维数组提前处理好区间[i,j]的最小值,这样可以O(1)查询,但当数据很大时,O(n^2)的空间开销无法承受。并且这样做在有更改操作时会变得非常麻烦。
线段树的做法。有一个O(n)的预处理,查询和更新操作均为O(logn),额外的空间复杂度是O(n)。
比如有一个[1,6]的二叉树。
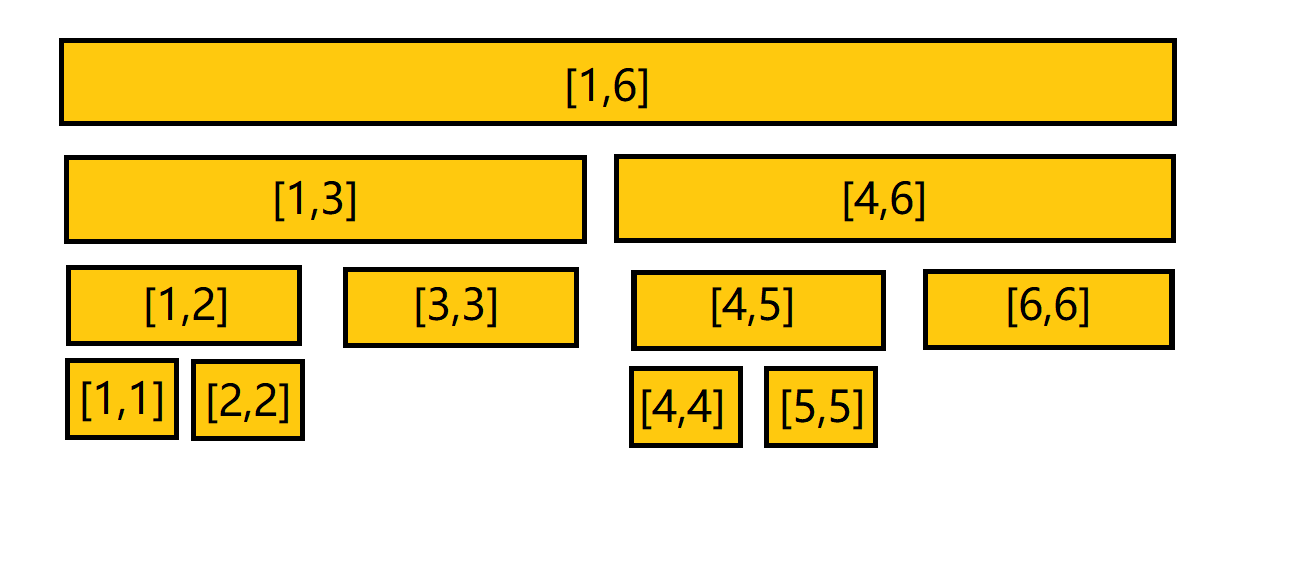
叶节点是原始数组中的元素,非叶节点代表所有子孙节点所在区间的最小值。由于线段树的父节点平均分割左右子树,所以线段树是完全二叉树。
*线段树的创建
数组模拟存储与链式存储。这里使用前一种。
定义包含n个节点的线段树int segtree_val[maxn],segtree_val[0]表示根节点,对于节点segtree_val[i],它的左儿子是segtree_val[2*i+1],右儿子是segtree[2*i+2]。
从根节点开始,平分区间, 递归的创建线段树。
这是优化之后的代码。
1 const int INF = 0x3f3f3f; 2 const int N = 1000; 3 int a[N]; 4 struct segment_tree{ 5 #define lson (o<<1) 6 #define rson (o<<1|1) 7 int sumv[N*4]; 8 int minv[N<<2],addv[N<<2]; 9 //存储线段树的区间和,一般二倍大即可,但有部分情况会超过二倍大小,所以开四倍大比较保险 10 inline void push_up(int o){ 11 sumv[o] = sumv[lson] + sumv[rson]; 12 } 13 inline void pushdown(int o){ 14 if (!addv[o]) 15 return; 16 } 17 inline void build(int o,int l,int r){ 18 if (l==r){ 19 sumv[o] == a[l]; 20 return ; 21 } 22 int mid = (l+r) >> 1; 23 build(lson,l,mid); 24 builf(rson,mid+1,r); 25 push_up(o); 26 27 } 28 inline int querymin(int o,int l,int r,int ql,int qr){ 29 if (ql <= l && r <= qr) 30 return sumv[o]; 31 int mid = (l+r) >> 1; 32 int ans = INF; 33 pushdown(o); 34 if (ql <= mid) 35 ans = min(ans,querymin(lson,l,mid,ql,qr)); 36 if (qr > mid) 37 ans = min(ans,querymin(rson,mid+1,r,ql,qr)); 38 return ans; 39 } 40 41 inline void change(int o,int l,int r,int q,int v){ 42 if (l==r){ 43 minv[o] += v; 44 return; 45 } 46 int mid = (l+r) >> 1; 47 if (q<=mid) 48 change(lson,l,mid,q,v); 49 else 50 change(rson,mid+1,r,q,v); 51 push_up(o); 52 } 53 54 inline void optadd(int o,int l,int r,int ql,int qr,int v){ 55 if (ql <= l && r <= qr){ 56 minv[o]+=v; 57 addv[o]+=v; 58 return ; 59 } 60 int mid = (l+r) >> 1; 61 pushdown(o); 62 if (ql <= mid) 63 optadd(lson,l,mid,ql,qr,v); 64 if (qr > mid) 65 optadd(rson,mid+1,r,ql,qr,v); 66 push_up(o); 67 } 68 };
*查询线段树
我们的任务是查找某个区间上的最小值,查询的思想是选出一些区间,让它们相连后恰好覆盖整个覆盖整个查询区间,因此线段树适合解决“相邻的区间的信息可以被合并成两个区间的并区间的信息”的问题。
*单节点更新
指只更新线段树的某个叶子节点的值,但是更新叶子节点会对其父节点产生一些影响,因此更新子节点后,要一并更新父节点的值。
*区间更新
指更新某个区间内的叶节点的值,因为涉及到的叶节点不止一个,而叶节点会影响相应的父节点,那么需要更新的父节点就会有很多,如果一次性更新完,性能是达不到要求的。
为此引入了线段树的懒惰标记概念。(lazy tag),这是线段树的精华所在。
懒惰标记:每个节点新增加一个标记,记录这个节点是否进行了某种修改(这种修改会影响子节点),对于任意区间的修改,先按照区间查询的方式将其划分成线段树的节点,然后去修改这些节点的信息,并给这些节点打上修改操作的标记。在修改和查询的时候,如果我们到了一个节点p,并且决定考虑其子节点,那么我们就要看节点p是否被标记,如果有,就要按照标记修改子节点的信息,并且给子节点都标上相同的标记,同时消掉节点p的标记。
因此需要在线段树结构中加入延迟标记区域,我们加入标记addv,表示节点的子孙节点在原来的值的基础上加上addv的值,同时还需要修改创建函数build和查询函数querymin,区间更新的函数为optadd。