tip:
卡特兰数是组合数学中经常出现在计数问题的数列,出栈次序是卡特兰数的一个应用。 我们将入栈视为 +1,出栈视为 -1,则限制条件为在任意位置前缀和不小于 0。
卡特兰数公式:
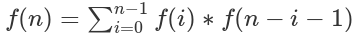
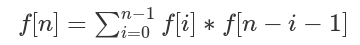
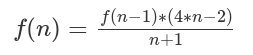
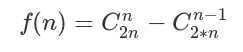
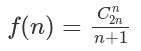
卡特兰数前几项为:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452。
实战:
T1:「BZOJ3907」网格
题干:
某城市的街道呈网格状,左下角坐标为 A(0,0),右上角坐标为 B(n,m),其中 n≥m。现在从 A(0,0) 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 (x,y) 都要满足 x≥y,请问在这些前提下,到达 B(n,m) 有多少种走法。
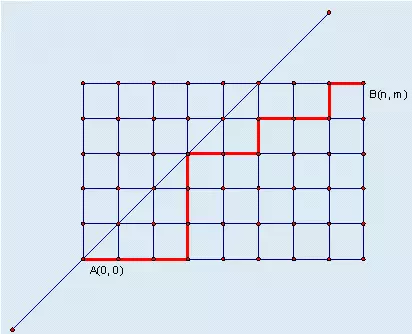
题解:
一道 catalan 裸题。但是 n 不一定等于 m,所以我们就需要变换一下 catalan 的式子。catalan 的定义式就是两个组合数相减的形式,是一个单步容斥。
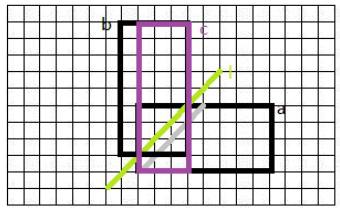
看一下上图,我们单步容斥减去的就是不合法的情况(紫框)。不合法的情况一定会碰到黄线,我们可以将碰到黄线以后的部分进行沿黄线翻折,这个翻折后的路径一定在紫框内,减去即可。即:
$ans=C_{n+m}^{n}-C_{n+m}^{m-1}$
(注意:高精减时注意开头的 0,高精乘低精时余数应是long long)
Code:

1 #include<cstdio>
2 #include<cstring>
3 #define $ 101010
4 #define ll long long
5 using namespace std;
6 int c1[$],c2[$],a1[$/10],a2[$/10],m,n,max1,max2,pr[$/10];
7 inline int max(int x,int y){ return x>y?x:y; }
8 inline void cut1(int x,int add){
9 for(register int i=2;i*i<=x;++i)
10 while((x%i)==0) x/=i,c1[i]+=add,max1=max(max1,i);
11 if(x>1) c1[x]+=add,max1=max(max1,x);
12 }
13 inline void cut2(int x,int add){
14 for(register int i=2;i*i<=x;++i)
15 while((x%i)==0) x/=i,c2[i]+=add,max2=max(max2,i);
16 if(x>1) c2[x]+=add,max2=max(max2,x);
17 }
18 inline void mul1(int yu=0){
19 a1[0]=a1[1]=1;
20 for(register int i=2;i<=max1;++i){
21 if(c1[i]==0) continue;
22 for(register int j=1;j<=c1[i];++j){
23 for(register int k=1,tmp=i;k<=a1[0];++k){
24 a1[k]=a1[k]*tmp+yu;
25 yu=a1[k]/10;
26 a1[k]%=10;
27 }
28 while(yu) a1[++a1[0]]=yu%10, yu/=10;
29 }
30 }
31 }
32 inline void mul2(int yu=0){
33 a2[0]=a2[1]=1;
34 for(register int i=2;i<=max1;++i){
35 if(c2[i]==0) continue;
36 for(register int j=1,tmp=i;j<=c2[i];++j){
37 for(register int k=1;k<=a2[0];++k){
38 a2[k]=a2[k]*tmp+yu;
39 yu=a2[k]/10;
40 a2[k]%=10;
41 }
42 while(yu) a2[++a2[0]]=yu%10, yu/=10;
43 }
44 }
45 }
46 inline void del(){
47 ll tmp=1,yu=0;
48 while(tmp<=a1[0]||tmp<=a2[0]){
49 if(a1[tmp]<a2[tmp]){
50 a1[tmp+1]--; yu=10;
51 }
52 pr[tmp]=a1[tmp]-a2[tmp]+yu; yu=0;
53 tmp++;
54 }
55 while(pr[tmp]==0&&tmp>1) tmp--;
56 pr[0]=tmp;
57 for(register int i=pr[0];i>=1;--i) printf("%d",pr[i]);
58 puts("");
59 }
60 signed main(){
61 scanf("%d%d",&n,&m);
62 for(register int i=n+1;i<=n+m;++i) cut1(i,1);
63 for(register int i=2;i<=m;++i) cut1(i,-1);
64 for(register int i=n+2;i<=n+m;++i) cut2(i,1);
65 for(register int i=2;i<=m-1;++i) cut2(i,-1);
66 mul1(); mul2(); del();
67 }
T2:「HNOI 2009」有趣的数列
题干:
我们称一个长度为 2n 的数列是有趣的,当且仅当该数列满足以下三个条件:
1、它是从 1 到 2n 共 2n 个整数的一个排列 {ai};
2、所有的奇数项满足 $a_1<a_3<⋯<a_{2n−1}$,所有的偶数项满足 $a_2<a_4<⋯<a_{2n}$;
3、任意相邻的两项 $a_{2i−1}$ 与 $a_{2i}$ (1≤i≤n) 满足奇数项小于偶数项,即:$a_{2i−1}<a_{2i}$
对于给定的 n,请求出有多少个不同的长度为 2n 的有趣的数列,输出答案 mod P 的值。
题解:
题目可化简为: 把所有数分成两组A、B,且排序后 Ai 始终比 Bi 小的方案数。
很像卡特兰数的模型,我们把 1~2n 写出来,显然可以有顺序地向里填,对于一个数 i,要么填 A 要么填 B。那么这个时候 A 集合的大小一定要小于 B 集合。这就是一个卡特兰数了。
本题其实就是从左往右扫每个数,把放在奇数项看作入栈,偶数看作出栈,符合 $catalan$ 使用模型。
(注意本题若只用唯一分解定理,会 T 得很惨。。。需要写一个线性筛,将每一个数的最小质因子预处理一下)
线筛:
1 inline void euler(){ 2 lst[1]=1; 3 for(register int i=2;i<=2*n;++i){ 4 if(judge[i]==0) prime[++cnt]=i, lst[i]=i; 5 for(register int j=1;j<=cnt&&1ll*i*prime[j]<=2ll*n;++j){ 6 judge[i*prime[j]]=1; 7 lst[i*prime[j]]=prime[j]; 8 if(i%prime[j]==0) break; 9 } 10 } 11 }
Code:

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #define $ 2100010 5 #define ll long long 6 using namespace std; 7 int c[$],n,lst[$],prime[$],cnt,maxx; 8 ll ans=1,mod; 9 bool judge[$]; 10 inline int max(int x,int y){ return x>y?x:y; } 11 inline ll modd(ll x){ return x-(x/mod*mod); } 12 inline void cut(int x,int add){ 13 while(x!=1) maxx=max(maxx,lst[x]), c[lst[x]]+=add, x/=lst[x]; 14 } 15 inline void eular(){ 16 lst[1]=1; 17 for(register int i=2;i<=2*n;++i){ 18 if(judge[i]==0) prime[++cnt]=i, lst[i]=i; 19 for(register int j=1;j<=cnt&&1ll*i*prime[j]<=2ll*n;++j){ 20 judge[i*prime[j]]=1; 21 lst[i*prime[j]]=prime[j]; 22 if(i%prime[j]==0) break; 23 } 24 } 25 } 26 inline int qpow(ll a,int x,ll sum=1){ 27 for(;x;x>>=1,a=a*a%mod) if(x&1) sum=modd(sum*a); 28 return (int)sum; 29 } 30 signed main(){ 31 scanf("%d%lld",&n,&mod); 32 eular(); 33 //for(register int i=1;i<=n;++i) printf("%d %d ",i,lst[i]); 34 for(register int i=n+2;i<=n*2;++i) cut(i,1); 35 for(register int i=2;i<=n;++i) cut(i,-1); 36 for(register ll i=2;i<=maxx;++i) 37 if(c[i]>0) ans=modd(ans*qpow(i,c[i])); 38 printf("%lld ",ans); 39 }
T3:「AHOI 2012」树屋阶梯
题干:
暑假期间,小龙报名了一个模拟野外生存作战训练班来锻炼体魄,训练的第一个晚上,教官就给他们出了个难题。由于地上露营湿气重,必须选择在高处的树屋露营。小龙分配的树屋建立在一颗高度为 N+1 尺的大树上,正当他发愁怎么爬上去的时候,发现旁边堆满了一些空心四方钢材,经过观察和测量,这些钢材截面的宽和高大小不一,但都是 1 尺的整数倍,教官命令队员们每人选取 N 个空心钢材来搭建一个总高度为 N 尺的阶梯来进入树屋,该阶梯每一步台阶的高度为 1 尺,宽度也为 1 尺。如果这些钢材有各种尺寸,且每种尺寸数量充足,那么小龙可以有多少种搭建方法?(为了避免夜里踏空,钢材空心的一面绝对不可以向上)
题解:
显然每个凸出来的角各自都是一块,只有一个是覆盖了左下角的,那么就会把这个阶梯分成两个阶梯子问题。就有:
$f[n]=f[0]*f[n-1]+f[1]*f[n-2]+…f[n-1]*f[0]$
我们还可以令 $C_n$ 表示用 n 个长方形拼成 $size$ 为 $n$ 的三角梯形的方案数。
我们枚举最左下角的点属于哪个长方形。显然有n种可能,每种方法又把剩下的部分分成两个三角梯形( $size$ 可能为 0 )
我们可以得到:
$Catalan_n = sum_{i = 0}^{n-1} Catalan_i * Catalan_{n-i-1}$
标准 $Catalan$ 方程。
Code:

1 #include<cstdio>
2 #include<cstring>
3 #include<cstdlib>
4 #define $ 1055
5 #define ll long long
6 using namespace std;
7 int m,n,k,t,c[$],maxx,prime[$],lst[$],cnt,a[$];
8 bool judge[$];
9 inline int max(int x,int y){ return x>y?x:y; }
10 inline void cut(int x,int add){
11 while(x!=1) maxx=max(maxx,lst[x]),c[lst[x]]+=add, x/=lst[x];
12 }
13 inline void eular(){
14 lst[1]=1;
15 for(register int i=2;i<=n*2;++i){
16 if(!judge[i]) prime[++cnt]=i, lst[i]=i;
17 for(register int j=1;j<=cnt&&i*prime[j]<=n*2;++j){
18 judge[i*prime[j]]=1;
19 lst[i*prime[j]]=prime[j];
20 if(i%prime[j]==0) break;
21 }
22 }
23 }
24 inline void mul(int yu=0){
25 a[0]=a[1]=1;
26 for(register int i=2;i<=maxx;++i){
27 while(c[i]--){
28 for(register int j=1;j<=a[0];++j){
29 a[j]=a[j]*i+yu;
30 yu=a[j]/10;
31 a[j]%=10;
32 }
33 while(yu) a[++a[0]]=yu%10, yu/=10;
34 }
35 }
36 for(register int i=a[0];i>=1;--i) printf("%d",a[i]);
37 }
38 signed main(){
39 scanf("%d",&n); eular();
40 for(register int i=n+2;i<=n*2;++i) cut(i,1);
41 for(register int i=2;i<=n;++i) cut(i,-1);
42 mul();
43 }
