OO 第三次博客作业(设计规格)
丁元杰 17231164
JML语言理论基础、应用工具链
JML常用于对bug容忍度极低的开发情形。其基本思想是使用无歧义的、程序可读的语言对类和方法的行为进行描述,从而达到准确传达架构师意图、并能够让程序在运行过程中进行检查的目的。这里用到的工具是OpenJML。
更进一步的,在完备的JML描述之后,使用到了JMLUnit自动化地对程序运行过程中对于规格的满足情况进行验证。
运行如下代码,进行检查和验证。
java -jar specsopenjml.jar -check SourceToCheck.java
java -jar specsopenjml.jar -esc SourceToCheck.java
java -jar specsopenjml.jar -rac SourceToCheck.java
java -jar specsjmlunitng.jar SourceToTest.java
java -jar specsopenjml.jar -d bin -rac SourceToTest.java
java -cp specsjmlunitng.jar:bin SourceToTest_JML_Test
运行结果如下:
srcMyPath.java:5: 警告: The prover cannot establish an assertion (NullField) in method MyPath
private /*@spec_public@*/ int[] nodes = null;
^
srcMyPath.java:24: 警告: The prover cannot establish an assertion (Postcondition: srcMyPath.java:22: 注: ) in method containsNode
return nodeSet.contains(node);
^
srcMyPath.java:22: 警告: Associated declaration: srcMyPath.java:24: 注:
//@ ensures
esult == (exists int i; 0 <= i && i < nodes.length; nodes[i] == node);
^
3 个警告
发现是JML无法验证基础数组:),遂放弃。
第九次作业: Path与PathContainer
程序度量
第九次作业的两个类互相引用,类图不具备参考价值。
设计架构
经观察,这次作业中较为纠结的部分即是如何建立Path到其id的双向映射。Path的特征类似于字符串:
- 可迭代
- 可比较(但是比较效率很低)
- 可散列(但是判等效率很低)
- 字符集为整型
因此,最为明智的方法是选择一种转为序列设计的集合(映射)结构——Trie树。由于Java的库中不包含这样的数据结构,因此手动实现一个即可。完成的功能十分单一:建立从Path到其id的映射。
自己程序的bug
本次作业在公测和互测阶段均未发现bug。
发现bug的策略
本次作业仍有很多同学使用了散列映射的方法完成从Path到id的映射,但是这个映射
(h:I_{32}^{2000}
ightarrow I_{32}),其中(I_{32})表示int类型所能表示的整数集合。听上去是一个重复率十分高的散列函数。致命的问题在于如果使用ArrayList类的默认hashCode,那么就会简单地使用31进制进行转换。如此一来,可以十分简单地构造出冲突的散列值。
理论上讲,散列表的正确性依赖于a.equals(b) => a.hashCode() == b.hashCode(),而效率则依赖于散列函数的随机性。可是这位同学使用hashCode相等去判断两个Path相等,那么就会在散列冲突的时候发生正确性问题。因此发现bug。
第十次作业: Path与Graph
程序度量
第十次作业的类图如下:

第十次作业的度量如下:
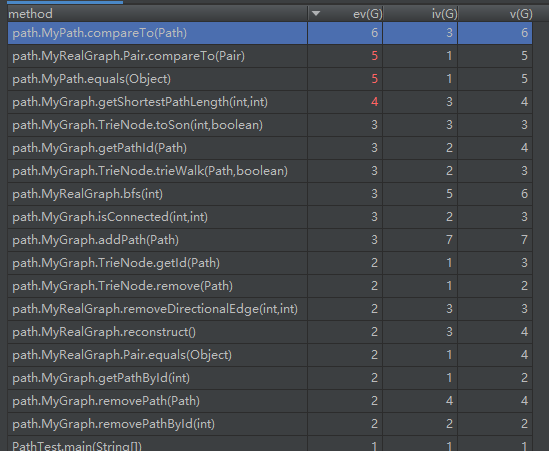
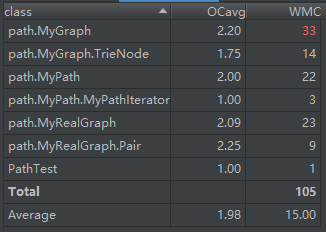
可以从类图中看出,为了实现寻找最短路、建立映射等功能,各个类还实现了自己各自的私有类。
设计架构
经观察,这次作业中的实现重点在于如何有效地计算两点之间的最短路。注意到这次的边权全部为1,因此最优的办法是使用BFS,其求出一个源的最短路的复杂度为(mathcal{O}(N+M))。在去除重边的情况下,在最坏的情况下和Floyd算法具有相同的复杂度。
考虑到Graph实际上只是一个Path的容器,同时不存在图论意义上的图,因此不宜将求解最短路的逻辑放于其中。于是单独设计了一个MyRealGraph类,用于建立图、计算和保存最短路。这道题目询问次数远远大于修改次数,因此可以在每次修改(添删边)之后对整个图进行重构+求解最短路,并将所有结果保存在一个Map中即可。
自己程序的bug
本次作业在公测和互测阶段均未发现bug。
发现bug的策略
本次作业没有发现别人的bug。
第十一次作业:Path与RailwaySystem
程序度量
第十一次作业的类图如下:

第十一次作业的度量如下:
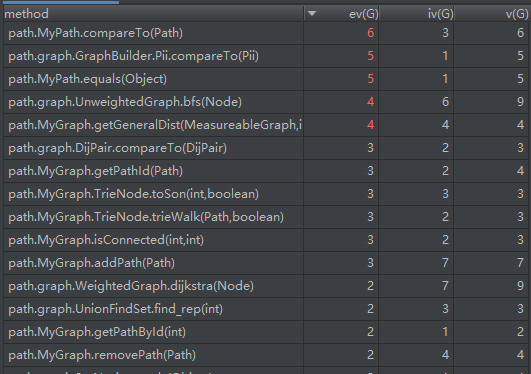
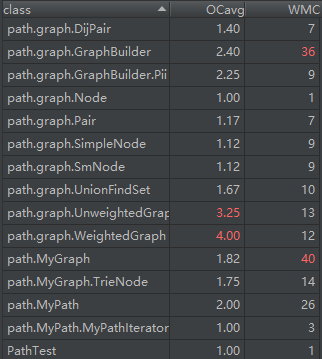
由类图可以看出,此次作业复杂程度最高的部分即是求解最短路相关的部分。为此还特地抽象了Node类和MeasuableGraph两个抽象类/接口。不过由于工厂GraphBuilder的存在,在此之外的结构十分清晰明了。
设计架构
架构
经观察,本次实现的难点在于四个最短(小)的度量。经过仔细分析,最短路、最少换乘、最小票价、最小不满意度可以统一使用最短路的模型,只需在点、边的配置上稍加修改即可。
可以确定的是,对于四个问题需要分别建图,但是每一张图向外的接口均为getShortestDist,因此可以使用接口进行抽象。同时,由于最短路已经使用更优的策略解决,剩余三个基本都应该使用一般的图,所以实际上实现BFS和Dijkstra算法的应当是实现该接口的若干实际类。
这样一看,四张图拥有了统一的模型,可以直接挂在RailwaySystem之中,不过仍有一个问题:四张图拥有完全不同的建立逻辑。于是这里使用了一个抽象工厂解决问题,工厂中负责记录重边等信息,在需要创建时根据内部的边的信息拆点、重构出四张图,只对外保留四种图的获取方法。最后将工厂挂在RailwaySystem之中即可。
算法
本次的算法采用了拆点+Dijkstra的算法。拆点是为了解决换乘的条件下,同一个站在不同地铁线上的出现应被视为图论中的不同的点的矛盾。因此最为朴素的思路即是将一个地铁站拆为它在所有地铁线中的出现。然而,如果暴力进行拆解,并对其两两连边,则有可能得到多达(50 imes 50 imes 80=200000)个换乘边,即便Dijkstra的(mathcal{O}left(Nleft(Nlog N+M ight) ight))也不能够容忍。因此,要找到更为明智的拆点方法。
对于每一个地铁站,引入换乘点的概念,地铁站拆出来的子点花费一定代价才能走到换乘点,然后换乘点再花费0代价走到各个子点。这样一来,因为拆点而新增的边数变为了(mathcal{O}(N))(地铁条数),并且一并解决了查询最短路时,选定何点为起始点的问题。
自己程序的bug
在公测与互测中,均为发现任何bug
发现bug的策略
在互测中,发现一个人的代码中使用了两点间的距离是否为1来判断是否存在两个点之间的连边,然后这显然不能正确处理自环的情形。于是精准爆破。