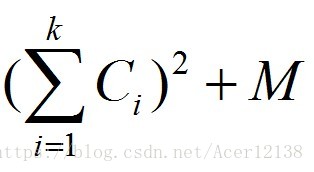HDU

题目标题：打印文章

给出N个单词，每个单词有个非负权值Ci，现在要将它们分成连续的若干段，每段的代价为此段单词的权值和的平方，还要加一个常数M，即。现在想求出一种最优方案，使得总费用之和最小。

输入格式

包含多组测试数据，对于每组测试数据。 第一行包含两个整数N和M（0<=N<=500000，0<=M<=1000）。 第2-N+1行为N个整数。

输出格式

输出仅一个整数，表示最小的价值。

样例输入

5 5
5
9
5
7
5
3 0
1
2
3

样例输出

230
14

思路 :
其实看到这个题就是dp 而且递推方程式为
dp[i] = min { dp[i] ,dp[j] + (sum[i] - sum[j])*(sum[i] - sum[j]) + m }
但是复杂度一估计直接爆炸，明显用这个方程式写出来的是一个二维的 dp 因此需要优化

如果对于 k 来说有一个更加优化的 j 的话 那么 可以得到
dp[j] + ( sum[i] - sum[j] ) ^ 2 + m > dp[k] + (sum[i] - sum[k] ) ^ 2 + m ;
移项化简可得
(dp[j] - dp[k]) + (sum[j] ^ 2 - sum[k] ^ 2) < 2 * (sum[j] - sum[k]) * sum[i];
令 up = (dp[j] - dp[k]) + (sum[j] ^ 2 - sum[k] ^ 2) , down = 2 * (sum[j] - sum[k])
那么 sum[i] = up (j ,k ) / down(j ,k ) ;
sum[i] 是前缀和因此sum数组是递增的，因此这个题可以用斜率优化

先看代码 :

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 5e5+50;

typedef long long ll;

ll dp[maxn] ,sum[maxn] ,v[maxn] ;
int n ,m ;
int que[maxn] ,head ,tail ;

ll getdp(int i ,int j ) { // dp
	return dp[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]) + m;
}

ll getup(int j ,int k ) { // up
	return dp[j] - dp[k] + sum[j] * sum[j] - sum[k] * sum[k] ;
}

ll getdown(int j ,int k ) { // down
	return 2 * ( sum[j] - sum[k] );
}

int main() {
	while( ~scanf("%d %d" , &n ,&m ) ) {
		memset(dp ,0 ,sizeof(dp));
		for (int i = 1 ; i <= n ; i ++ ) {
			scanf ("%lld",&v[i]);
			sum[i] = sum[i-1] + v[i];
		}
		head = tail = 0; dp[tail ++] = 0; // 不可以从 1 开始进入队列，因为前缀和是从 0 开始的
		for (int i = 1 ; i <= n ; i ++ ) {
			while(head + 1 < tail && getup(que[head+1] ,que[head]) < getdown(que[head+1] ,que[head]) * sum[i] ) head ++ ;
			dp[i] = getdp(i ,que[head] ) ;
			while(head + 1 < tail && getup(que[tail-1] ,que[tail-2]) * getdown(i ,que[tail-1]) >= getup(i ,que[tail-1]) * getdown(que[tail-1] ,que[tail-2])) tail --;
			que[tail ++] = i;
		}
		printf("%lld
",dp[n]);
	}
	return 0;
}

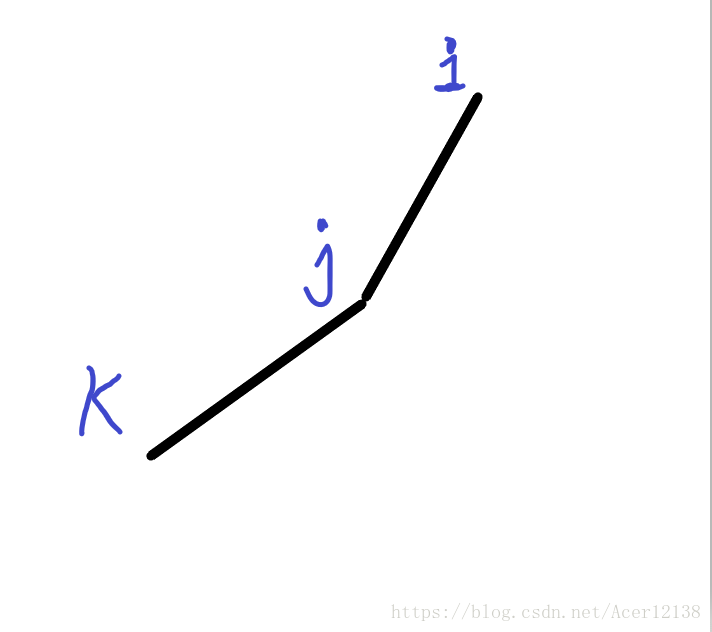
1 ) , 我们来看for循环里面的第一个 while 就相当于在que[head] 后面还有 比 que[head] 更加优化情况因此每次都要 head ++ ,属于这种情况 :

此时 i 为我们待求的 ，k 为que[ head ] , j 为 que[head + 1] 明显 j要比 k更加优化

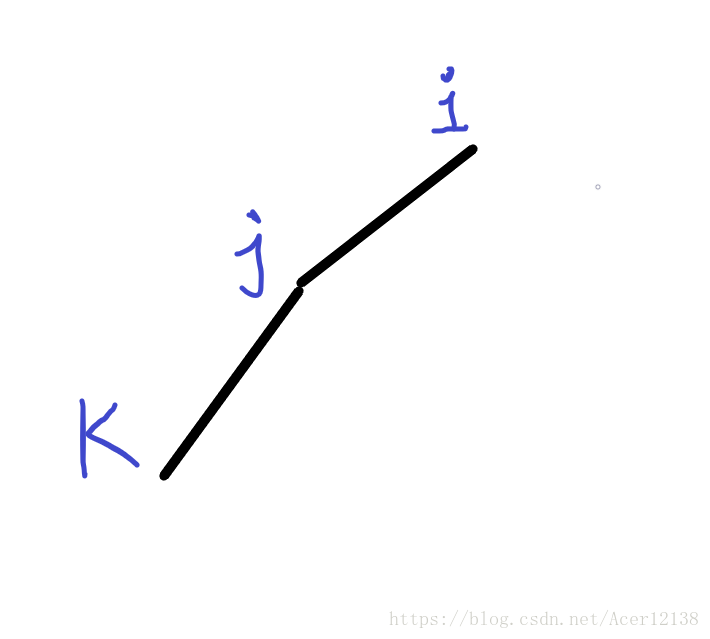
2 ) , 对于第二个while 循环 可以这样理解 当前的 i 如果要加入队列的话必须保持队列的斜率是单调递增的

这种情况就是 i 是当前待加入的 ， j 代表 que[tail-1] , k 代表que[tail-2] , 这种情况下 j 是明显不符合条件的因此要舍去 j , tail –