首先理解堆排序:
堆:
堆栈是计算机的两种最基本的数据结构。堆的特点就是FIFO(first in first out)先进先出,这里的话我觉得可以理解成树的结构。堆在接收数据的时候先接收的数据会被先弹出。栈的特性正好与堆相反,是属于FILO(first in/last out)先进后出的类型。栈处于一级缓存而堆处于二级缓存中。这个不是本文重点所以不做过多展开。
思想:
本质是使用大根堆或小根堆来对一个数组进行排序。所以首先要理解树的概念,若是不太理解树的概念可以自行百度。
完全二叉树:
堆是一种完全二叉树,就是除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐的树。就像码金字塔的砖块,必须从头到底,从左到右一个一个码,不能空缺。。
大根堆小根堆定义:
大根堆:每个结点的值都大于或等于左右子结点
小根堆:每个结点的值都小于或等于左右子结点
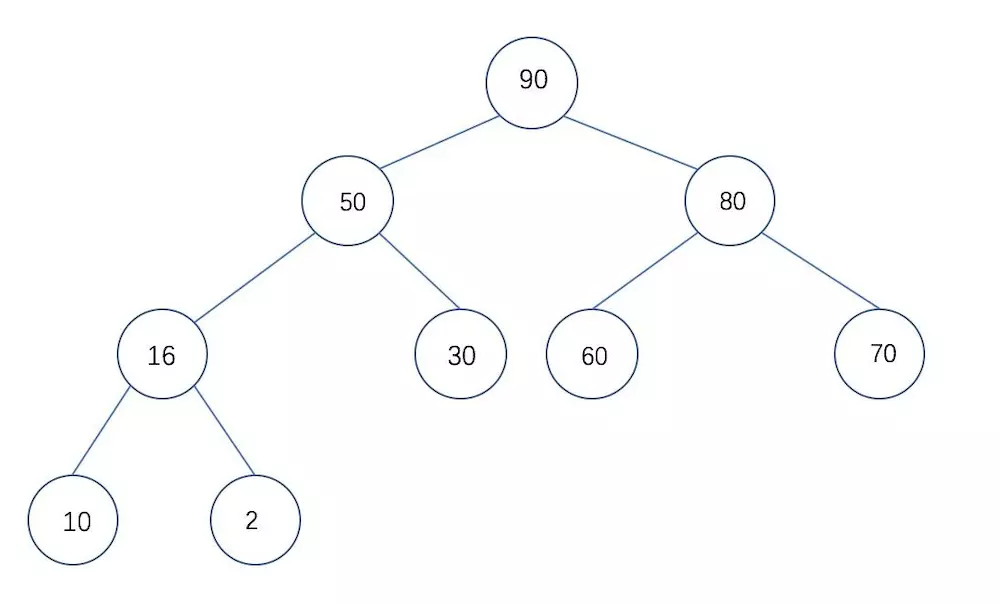
大根堆
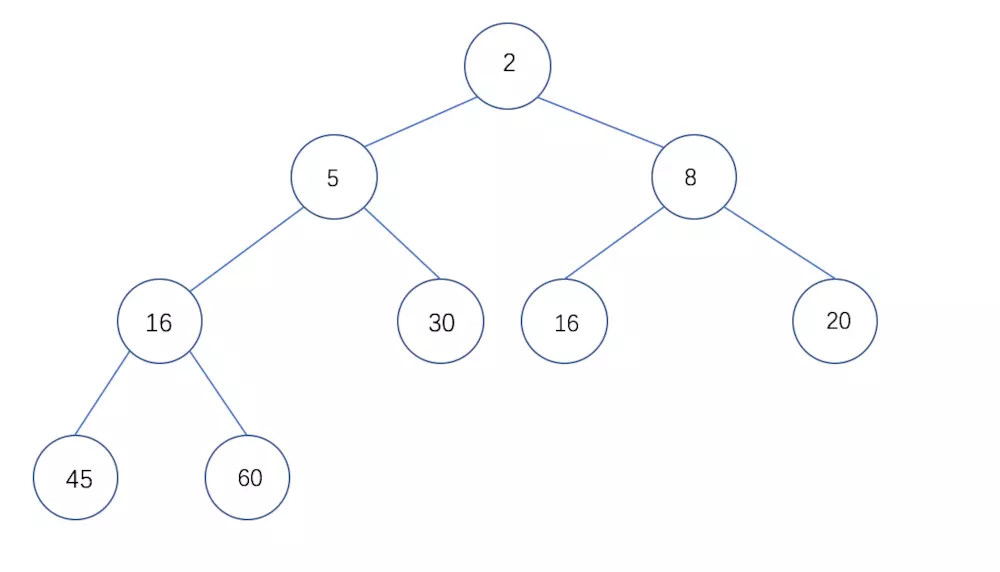
小根堆
关于数组下标
将一个数组构建成二叉树的结构,那么对于其中某一个元素的index假设为n,满足以下条件:
1)它的父节点若存在,父节点的index为n//2(n//2指n除以2取整数)
2)若是左子节点存在,index为2*n
3)若是右子节点存在,index为2*n+1
注意:以上条件是在index是从1开始才满足,所以在后面计算中会在数组第一个位置添加一个[0]作为占位元素。
操作步骤:
以由对数组从小到大进行排序的情况,需要构建大根堆。
1.首先将整个数组进行构建一个大根堆得到[0,R1,....,Rn](具体实现后面讲)
2.由于R1是最大的数,所以把R1与Rn改变位置,变成[0,Rn,...,Rn-1,R1],此时[0,Rn...,Rn-1]是无序的,[R1]是有序的
3.对数组[0,Rn...,Rn-1]进行重构大根堆,得到[0,R2,....,Rn-1]
4.由于R2是最大的数,所以把R2与Rn-1改变位置,变成[0,Rn-1,...Rn-2,R2,R1],此时[0,Rn-1...,Rn-2]是无序的,[R2,R1]是有序的
5.重复以上步骤,直到无序列表只有[0],最终得到的有序序列则是按照从小到大规律排列的。
为了能更好的理解上面的话,我推荐看b站这个视频演示。。https://www.bilibili.com/video/av18980178?from=search&seid=3518072115040122033
代码:
1 import math,random 2 3 #网上找的打印树的一个函数,很好用,谁用谁知道 4 def print_tree(array): #打印堆排序使用 5 ''' 6 深度 前空格 元素间空格 7 1 7 0 8 2 3 7 9 3 1 3 10 4 0 1 11 ''' 12 # first=[0] 13 # first.extend(array) 14 # array=first 15 index = 1 16 depth = math.ceil(math.log2(len(array))) # 因为补0了,不然应该是math.ceil(math.log2(len(array)+1)) 17 sep = ' ' 18 for i in range(depth): 19 offset = 2 ** i 20 print(sep * (2 ** (depth - i - 1) - 1), end='') 21 line = array[index:index + offset] 22 for j, x in enumerate(line): 23 print("{:>{}}".format(x, len(sep)), end='') 24 interval = 0 if i == 0 else 2 ** (depth - i) - 1 25 if j < len(line) - 1: 26 print(sep * interval, end='') 27 index += offset 28 print() 29 30 def sort(arr,start,end): 31 if end == start * 2: 32 if arr[start * 2] > arr[start]: 33 arr[start * 2], arr[start] = arr[start], arr[start * 2] 34 else: 35 if end < start * 2 + 1: 36 return 37 else: 38 left = arr[start*2] 39 right = arr[start*2+1] 40 if left>right and left > arr[start]: 41 arr[start * 2 ], arr[start] = arr[start], arr[start * 2 ] 42 sort(arr,start*2,end) 43 if left<right and right > arr[start]: 44 arr[start * 2+1], arr[start] = arr[start], arr[start * 2+1] 45 sort(arr, start * 2+1, end) 46 47 def heapfiy(arr): 48 x = len(arr) - 1 49 n = x // 2 50 while n > 0: 51 # print(n) 52 sort(arr, n, x) 53 n -= 1 54 55 #以下是主函数 56 57 #第一个0是占位用 58 orignal_list=[0, 74, 73, 59, 72, 64, 69, 43, 36, 70, 61, 40, 16, 47, 67, 17, 31, 19, 24, 14, 20, 48, 5, 7, 3, 78, 84, 92, 97, 98, 99] 59 print(orignal_list) 60 #第一次构建最大堆 61 heapfiy(orignal_list) 62 #打印树 63 print_tree(orignal_list) 64 65 x= len(orignal_list) - 1 66 while x!=1: 67 #交换最大的数和最后一个 68 orignal_list[1],orignal_list[x]=orignal_list[x],orignal_list[1] 69 x-=1 70 #由于交换了,不再是最大堆,重新构建最大堆 71 n=x//2 72 while n>0: 73 sort(orignal_list,n,x) 74 n-=1 75 76 #打印最后结果 77 print_tree(orignal_list) 78 print(orignal_list)
结果如下