题目链接:https://www.luogu.com.cn/problem/P5021
首先介绍一个东西:multiset。它可以看成一个有序的序列,且允许存在重复的数,并支持logn的时间插入和删除。(其他:https://blog.csdn.net/sodacoco/article/details/84798621)
看到题面,首先想到的是二分答案。二分第m条的长度,判断的话就看是否至少存在有m条路径,使得路径长度大于等于mid。
怎样每次找的都是尽可能大的呢?那就得在树上贪心。
贪心策略:
对于经过一个点的赛道的构建方式有且只有两种:
1.一条链直接作为赛道(如下图中类似于红色的构建方式)。
2.两条半链拼成一个赛道。
因此可以对于以u为根的子树,先尽可能多的拼出赛道,同时在剩下拼不成整条赛道的情况下,选尽量长的传给父节点,作为父节点半链的候选答案。
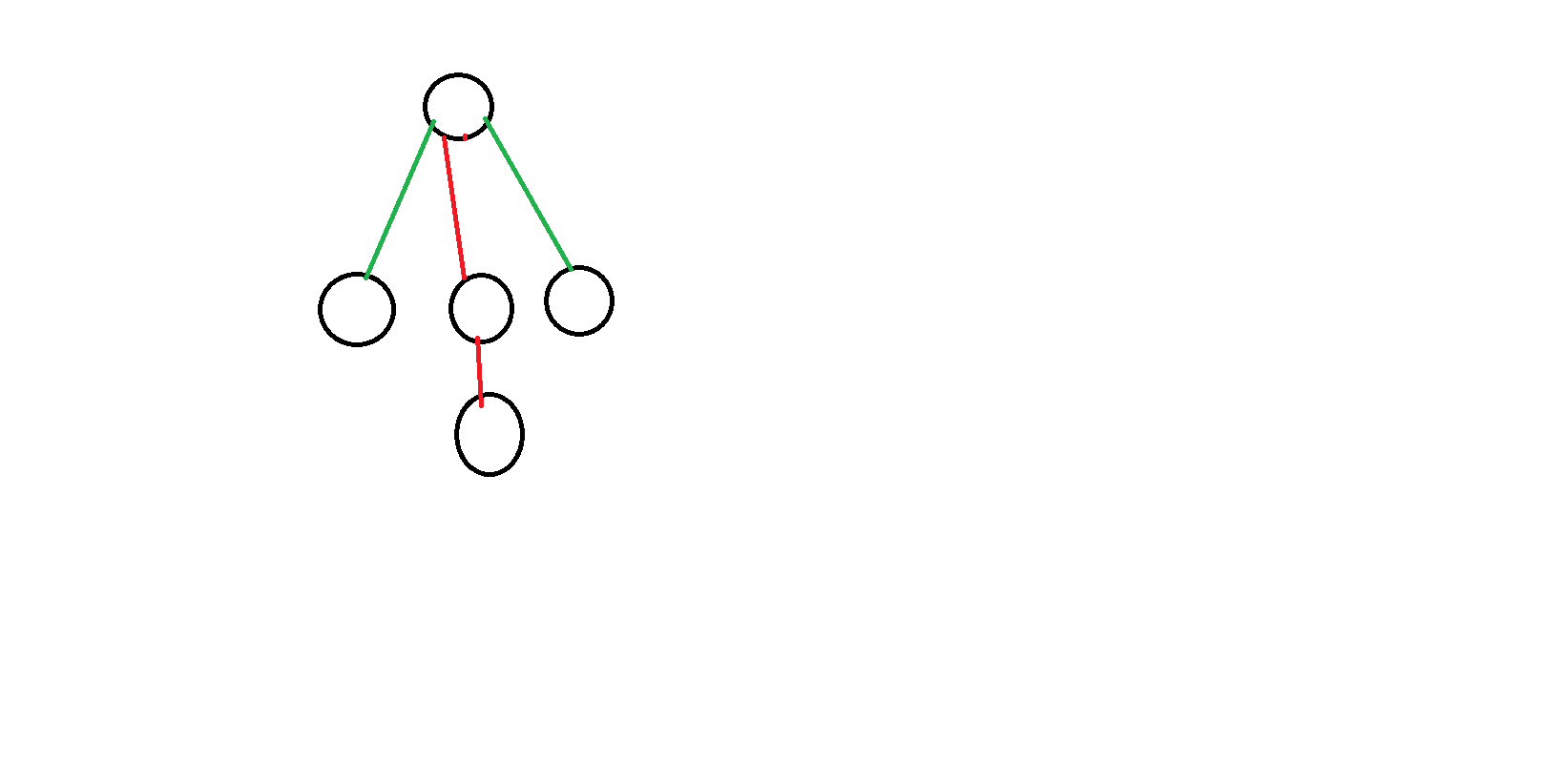
如何处理半链的拼接呢?把它放到multiset中进行维护,二分寻找最短的与当前长度的半链可以拼成整链的半链,如果找不到就一直取最大值,把最大的传上去即可。
AC代码(O2):

1 #include<cstdio> 2 #include<iostream> 3 #include<set> 4 #include<cstring> 5 using namespace std; 6 int n,m,tot,num; 7 const int N=50005; 8 multiset<int> st[N]; 9 multiset<int>::iterator it1,it2; 10 struct node{ 11 int to,next,w; 12 }edge[N<<1]; 13 int head[N]; 14 void add(int u,int v,int w){ 15 edge[tot].to=v; 16 edge[tot].next=head[u]; 17 edge[tot].w=w; 18 head[u]=tot++; 19 } 20 int DFS(int u,int fa,int x,int dis){ 21 st[u].clear(); 22 for(int i=head[u];i!=-1;i=edge[i].next){ 23 int v=edge[i].to; 24 if(v==fa) continue; 25 int w=DFS(v,u,x,edge[i].w); 26 if(w>=x) num++; 27 else st[u].insert(w); 28 } 29 int maxx=0; 30 if(st[u].size()==0) return dis; 31 while(st[u].size()){ 32 it1=st[u].begin(); 33 int w=*it1; 34 st[u].erase(it1); 35 it2=st[u].lower_bound(x-w); 36 if(it2!=st[u].end()){ 37 num++; 38 st[u].erase(it2); 39 } 40 else maxx=max(maxx,w); 41 } 42 return dis+maxx; 43 } 44 bool check(int x){ 45 num=0; 46 DFS(1,0,x,0); 47 return num>=m; 48 } 49 int main(){ 50 memset(head,-1,sizeof(head)); 51 scanf("%d%d",&n,&m); 52 for(int i=1;i<n;i++){ 53 int u,v,w; 54 scanf("%d%d%d",&u,&v,&w); 55 add(u,v,w); add(v,u,w); 56 } 57 int l=1,r=1e9; 58 while(l<r){ 59 int mid=(l+r+1)>>1; 60 if(check(mid)) l=mid; 61 else r=mid-1; 62 } 63 printf("%d",l); 64 return 0; 65 }
