题目链接:https://www.luogu.com.cn/problem/P2168
哈夫曼编码:
有n个字符,a,b,c,...,每个字符都有一个频率,$f_a,f_b,f_c...$,用k进制数表示字符a,b,c...
设计编码,使得总长度Len最短,其中$Len=f_a imes l_a+f_b imes l_b...$
不难发现,如果每个字符都有自己的表达方式,那么任意两个编码之间不能是对方的前缀,表现在树上就是不能是它的祖先(不在到根节点的路径上)。
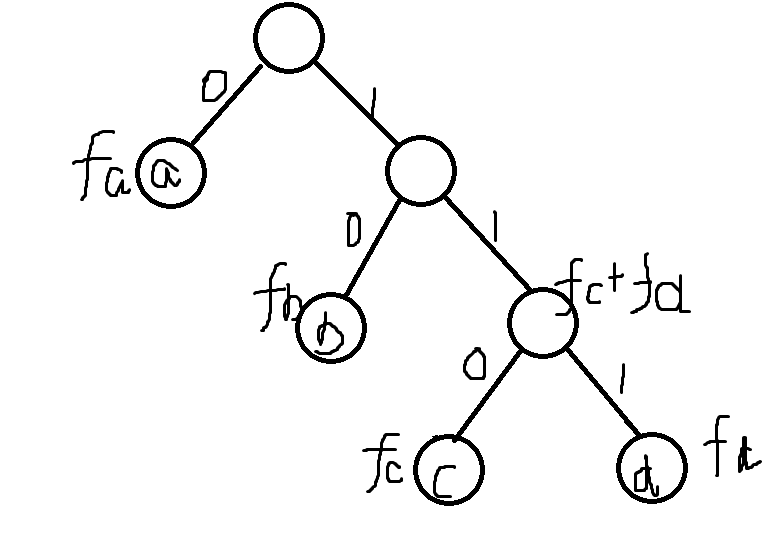
性质:1.字符是叶节点。
2.非叶节点有k个子节点。(这样一定是最优的)
2‘.非叶节点中子节点数量不是k的至多有一个。(当(n-1)%(k-1)==0时没有)
所以可以添加一些(k-1-(n-1)%(k-1))f为0的字符,使其满足性质2,且不会产生影响。
所以在k进制下,最优的操作就是每次取前k个最小的,合并。
例题:
1.合并果子
题目链接:https://www.luogu.com.cn/problem/P1090
其实可以看成是一个2进制下的哈夫曼编码问题,搬运花费即为频率,每次合并取前两个最小的。
2.荷马史诗
题目链接:https://www.luogu.com.cn/problem/P2168
k进制下的哈夫曼编码问题。首先看能否满足性质二,不满足则用w为0的字符补全,然后每次取k个合并(想哈夫曼树),即得答案。
AC代码:

1 #include<cstdio> 2 #include<iostream> 3 #include<queue> 4 #include<algorithm> 5 using namespace std; 6 typedef long long ll; 7 ll n,k,cnt,sum,ans; 8 struct node{ 9 ll w,h; 10 }; 11 bool operator<(node a,node b){ 12 if(a.w!=b.w) return a.w>b.w; 13 return a.h>b.h; 14 } 15 priority_queue<node> q; 16 int main(){ 17 scanf("%lld%lld",&n,&k); 18 for(int i=1;i<=n;i++){ 19 node t; 20 scanf("%lld",&t.w); 21 t.h=1; 22 q.push(t); 23 } 24 ll top=0; 25 if((n-1)%(k-1)!=0){ 26 int t=k-1-(n-1)%(k-1); 27 top+=t; 28 for(int i=1;i<=t;i++){ 29 node t; 30 t.w=0;t.h=1; 31 q.push(t); 32 } 33 } 34 top+=n; 35 while(top!=1){ 36 ll maxh=0; 37 sum=0; 38 for(int i=1;i<=k;i++){ 39 node t; 40 t=q.top(); 41 q.pop(); 42 maxh=max(maxh,t.h); 43 sum+=t.w; 44 } 45 ans+=sum; 46 node t; 47 t.w=sum; t.h=maxh+1; 48 q.push(t); 49 top-=k-1; 50 } 51 printf("%lld %lld",ans,q.top().h-1); 52 return 0; 53 }
